プラズマとは何か？

～宇宙の基本要素～

公開日：2021 年 4 月 17 日
最終更新日：2021 年 4 月 17 日

電荷を持った粒子から成る気体をプラズマと言います。太陽はプラズマの塊です。更に、宇宙に存在する解明された物質のほとんどはプラズマの状態にあると言われています。本記事では、宇宙にある様々なプラズマ系を紹介した後、プラズマの定義や種類について説明します。

目次

※ 記事は下に行くほどマニアックな内容になります。

※ マニア度：低 中 高 超

太陽は電気を通す気体

太陽は水素とヘリウムから成る気体の塊です。ただし、例えば地球大気のような通常の気体とは異なり、電気を通しやすいという性質を持ちます。言い換えると、電気抵抗が物凄く小さいということです。この性質は太陽で起きる現象を考える上でいちばん重要であり、このサイトの他の記事でも説明のキーポイントになっています。

例えば身の回りの地球大気 (\(\text{N}_2\) と \(\text{O}_2\) の混合気体) は基本的に電気を通しません。雷雲や静電気が溜まったドアノブに指を近づけたときのように、大きな電圧がかかると瞬間的に雷のような放電現象が起きます。これは例外的な現象であり、常日頃から我々の周りを電流が飛び交っているわけではありません。しかし、太陽を構成する気体の中では容易に電流が発生します。

太陽の具体的な状態

先ほど太陽は水素とヘリウムから成ると述べました。日常の温度での水素は、例えば水の電気分解で生成され、火をつけると爆発する気体です。身の回りのヘリウムは、宙に浮かぶ風船に入っていたり、吸うと声が高くなるジョークグッズに含まれている気体です。

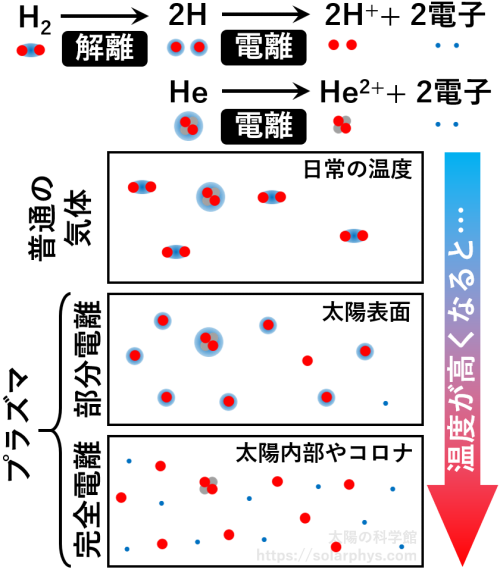
これらの気体は \(\text{H}_2\) 分子や \(\text{He}\) 原子がたくさん (\(1 \ \text{cm}^{3}\) あたりに \(10^{19}\) 個の桁数) 飛び交っている状態です ( 図 1 の最上段 )。これらの粒子は原子核の電荷を打ち消す数の電子を束縛しているので、電荷を持ちません (中性粒子)。

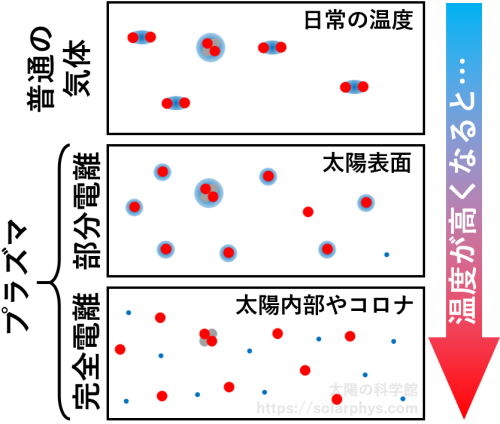
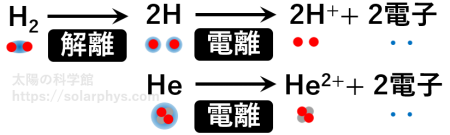
図 1   各領域での水素とヘリウムの状態：赤丸は陽子、灰色の丸は中性子、青色は電子を想定して描かれている。

\(\text{H}_2\) 分子や \(\text{He}\) 原子は、温度が高くなると束縛していた電子を手放し、正の電荷を持つ粒子として存在するようになります。また、手放された電子は負の電荷を持つ独立した粒子として振舞います。これを電離 (ionization) と言います ( 図 2 )。

どの温度で電離するのかは気体の密度にも依るので、一概には言えませんが、太陽内部やコロナの環境ではほとんどの粒子が電離した状態で存在しています ( 図 1 の最下段 )。あるいは、太陽表面付近では丁度水素が電離するかしないかの瀬戸際の温度 (約 6000 K, ケルビン 脚注 [ケルビン]：温度の単位には基本的にケルビン (K) を用います。日常で使われる摂氏と目盛の幅は同じであり，摂氏 0 度は 273.15 K です。つまり，例えば 300 K は摂氏 26.85 度のことです。 ) なので、一部の水素だけが電離した状態で存在しています ( 図 1 の中段 )。

図 2   水素とヘリウムの電離

このように、太陽は電荷を持った粒子 (荷電粒子) を含む気体であり、プラズマ (plasma) と呼ばれるものの一種です。特に、太陽内部やコロナのようにほとんどの粒子が電離した状態のプラズマは完全電離プラズマ (perfectly/fully ionized plasma) と呼ばれます。対して、太陽表面のようにほとんどの粒子は中性で、一部の粒子だけが電離しているプラズマは部分電離 (弱電離) プラズマ (partially/weakly ionized plasma) と呼ばれます。

後に紹介するように、プラズマは宇宙に普遍的に存在しています。太陽はその中の典型例であり、地球に住む我々がつぶさに観察できる貴重な系です。太陽研究はプラズマ物理学の発展に大きく貢献してきました。

電流と磁場

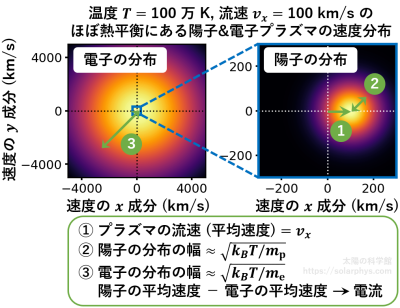
太陽は \(\text{H}^+\) や \(\text{He}^{2+}\) のような陽イオンと (独立した) 電子から成ると述べました。ある瞬間を切り取ると、各々の粒子は勝手な方向に運動しています ( 図 3 )。記事「温度とは何か？：流体力学の前提」で説明する 熱運動 脚注 [熱運動]：気体 (プラズマ) を構成する粒子たちの平均速度をその気体の流速と言います。流速と共に移動する観測者から見ても、各粒子たちはそれぞれ勝手な方向に運動しています。これを熱運動と言います。その速度分布の幅が温度です。具体的には、例えば電子の熱運動の速さの平均を \(\overline{v}_\text{e}\) としたとき、電子 1 個の持つ平均的な運動エネルギー \(m_\text{e}\overline{v}_\text{e}^2/2\) が \(k_BT_\text{e}\) に相当します。\(T_\text{e}\) は電子の温度です。ボルツマン定数 \(k_B = 1.38\times 10^{-23} \ \text{J K}^{-1}\) は温度とエネルギーの単位換算のための物理定数です。 です。

各々の粒子が持つ速度を沢山の粒子について平均した値を気体の流速と言います ( 図 3 A )。ただし、細かいことを言うと、粒子の質量で重み付けした平均です。太陽の場合、陽イオンの質量は電子の 1000 倍以上大きいので、ほとんど陽イオンの平均速度が気体の流速ということになります。

図 3   気体の流速と電流の定義

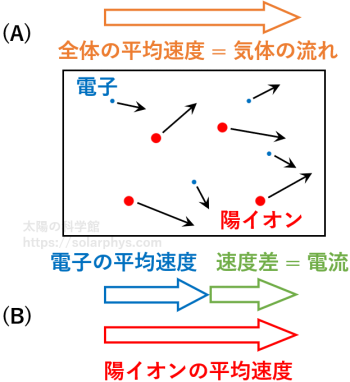
一方で、陽イオンの平均速度と電子の平均速度に差があった場合、そこには「電流が存在する」と言います。言い換えると、電子の平均速度で移動する観測者から見た陽イオンの平均速度が電流です。

気体に電流が流れると、その周りには磁場が存在しなければなりません。アンペールの法則です。磁場の中を気体が流れると、電磁誘導によって磁場の様子は変化します。また、磁場と電流が存在すると、各粒子が受ける ローレンツ力 脚注 [ローレンツ力]：電荷を持った粒子が磁場の中を運動をすると図の向きにローレンツ力を受けます。太陽を構成するプラズマ ( = 電気を通しやすい気体) は荷電粒子の集団であるため、電流 ( = 陽イオンと電子の間の相対的な動き) が発生すると各粒子にはたらくローレンツ力の合計としての力を受けることになります。単位体積あたりにはたらくローレンツ力 (単位 \(\text{N/m}^3\)) は電流 (単位 \(\text{A/m}^2\)) と磁場 (単位 \(\text{T}\)) の外積になります。 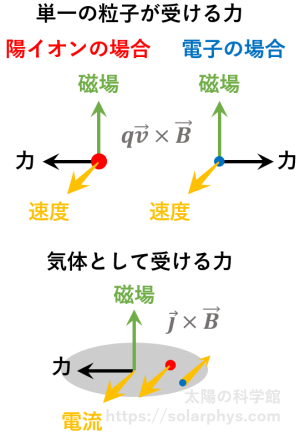の合計としての力を気体が受けることになります。

このように、プラズマでは物質粒子の集団 (気体) と電磁場が常に複雑な相互作用をしています。詳しくは記事「プラズマと磁場：磁力線が「実体」を帯びる」で説明します。その結果として、このサイトの他の記事で説明している様々な現象が起きます。

太陽を考える際は、高校で習う力学の延長にある 流体力学 脚注 [流体力学]：液体や十分に濃い気体の速度、温度、圧力や密度などの時間発展を計算するための理論を流体力学と言います。 という理論と電磁気学の理論が必要になります。太陽物理学では、これらの理論を融合させた 磁気流体力学 脚注 [磁気流体力学]：液体や十分に濃い気体の速度、温度、圧力や密度などの時間発展を計算するための理論を流体力学と言います。特に、プラズマのような電気を通す流体を記述するために、流体力学と電磁気学を融合させた理論を磁気流体力学 (MHD) と言います。 (MHD) という理論を用いて、観測される現象を説明することになります。逆に言うと、これらの基礎理論が太陽の場合にも適用できるのかどうかをチェックする場でもあるわけです。

身の回りのプラズマ

身の回りにあるプラズマの代表例は蛍光灯です。点灯中の蛍光灯の内部では、封入された希ガスが電離しており、電流が流れています。他にも溶接や集積回路の刻印のような工業用途でプラズマ (放電現象) が用いられることもあります。

雷

自然現象で発生するプラズマの代表例は雷です。落雷は \(10^{-6}\) 秒程度の短い時間スケールで起きる現象です。図 4 はフロリダ工科大学が YouTube にアップロードしている動画です。落雷の様子がスローモーションで捉えられています。

図 4   スローモーションで捉えられた落雷の様子：提供 Florida Institute of Technology.

雲の底に負の電荷が溜まった場合、地面との間に高電圧が発生します。すると、雲底に存在する電子の一部が地面に向かって高速で流れ始めます。電子は直ぐに大気を構成する窒素分子 \(\text{N}_2\) や酸素分子 \(\text{O}_2\) と衝突します。例えば次式のような反応が起きて電子はどんどん増殖していきます。式中の \(e^-\) は電子のことです。

\begin{align} \text{O}_2 + e^- &\longrightarrow \text{O}^+_2 + 2e^- \\ \text{N}_2 + e^- &\longrightarrow \text{N}^+_2 + 2e^- \end{align}

高速の電子にぶつかられた大気は温度を上げていき、数千 K になると次式のような反応も起き始め、弱電離プラズマと呼べる状態に近づいていきます ( da Silva & Pasko, 2013 )。

\[\text{N} + \text{O} \longrightarrow \text{NO}^+ + e^-\]

これが、図 4 の動画で雲から地面に向かって光が伸びていく段階の状態です。伸びていく光 (前駆放電, leader) の領域ではイオンや電子の数が増えているため、電気抵抗が小さくなっています。こうして、大気中に電流の通りやすい道が形成されていきます。

やがて前駆放電が地面に近づくと、いわば地面と雲が通電した状態になり、地面から雲に向けて数万 \(\text{A}\) (アンペア) の大電流が流れます (帰還雷撃, return stroke)。電流の流れている領域はいわゆるジュール熱によって数万 K の高温になり、大気は膨脹して雷鳴が響き、激しい閃光 (稲妻) が見えます。

この段階になると、弱電離プラズマと言える状態になっています ( 例えば da Silva et al., 2019 )。稲妻は大気が電離して発生したプラズマから発せられる光を見ているわけです。

熱核融合炉

もうひとつ、「身の回りの」プラズマとは言えませんが、次世代の電力源の候補として進められている熱核融合炉の研究もプラズマ物理学の発展に大きく貢献してきました。この文脈では、磁場を操ることで、高温のプラズマを安定して (エネルギーロスが少なくなるように) 長時間、炉の中に閉じ込めるための研究が行われています。

日本では、例えば 量子科学技術研究開発機構 が ITER という国際プロジェクトに参加しているほか、核融合科学研究所 や 筑波大学 プラズマ研究センター のような機関でも、それぞれ独自の方法で研究が進められています。

例えば ITER では、図 5 のようなドーナツ型 (トカマク型) の真空容器内に超電導コイルを用いて \(10 \ \text{T}\) ( テスラ 脚注 [テスラ]：磁場の強さを表す単位です。理想的には磁力線の密集度に相当しますが、実際の図では特徴的な磁力線だけを間引いて描くため、この限りではありません。磁場の強さの単位には \(\text{G}\) (ガウス) が使われることもあり、\(1 \ \text{G}=10^{-4} \ \text{T}\) です。 ) の強力な磁場を発生させ、プラズマを閉じ込めます。これは プラズマと磁場 の記事で説明しているように、プラズマが 磁力線 脚注 [磁力線]：各場所での磁場の向きを繋げた曲線を磁力線と言います。理想的には磁力線の密集度がその場所での磁場の強さ (単位 T, テスラ) を表しますが、実際の図では特徴的な磁力線だけを間引いて描くため、この限りではありません。磁力線が分裂したり合流したりすることはありません。電気を通すプラズマでは磁力線は物質に凍結している (物質は磁力線に垂直な方向に動くことができない) ので、磁力線の動きはその場所でのプラズマ (物質) の動きを表します。 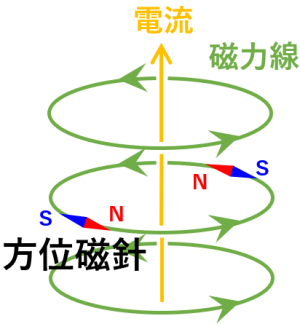に垂直な方向に動くことができないという性質を利用した装置です。

図 5   ITER 計画でフランスに建設される予定の熱核融合炉の断面図：提供 ITER Organization .

磁力線の「かご」の中には重水素イオン (\(\text{D}^+\)) と 三重水素イオン (\(\text{T}^+\))、電子から成るプラズマが注入され、 1 億 K を超える温度まで加熱されます。プラズマを十分な時間 (数百秒程度) 磁力線内に閉じ込めておくことができれば、 図 6 (A) の反応が起きると予想されています。この反応では反応前の2 粒子が持っていた質量の一部が反応後の 2 粒子の持つ運動エネルギーに変換されます。

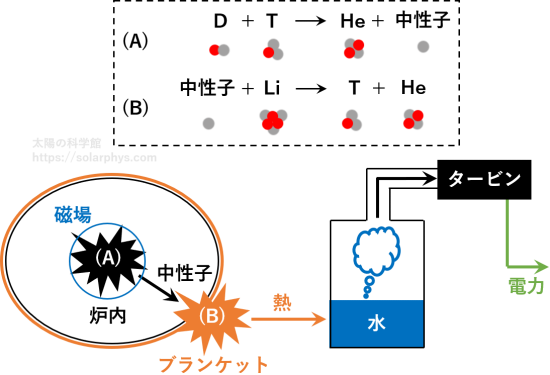
図 6   ITER で計画されている核融合発電の様式：反応式について、赤丸は陽子、灰色の丸は中性子を想定して描かれている。

図の (A) の反応で発生した中性子は電荷を持たないため、磁力線のかごから飛び出します。そして、炉の壁に設置されたブランケットという装置に吸収されます。これにより、ブランケットは加熱されると同時に、図の (B) のような反応を起こし、(A) の反応で使われる三重水素 (\(\text{T}\)) を再び生成することが期待されます。

後は、ブランケットで発生した熱を用いて湯を沸かし、その蒸気の圧力でタービンを回すことにより発電します。まとめると、重水素と三重水素がヘリウムに変わる際に発生する余剰エネルギーを用いて発電する仕組みです。磁場閉じ込めによる熱核融合発電についてより詳しくは、例えば Zohuri (2017) を読んでください。

宇宙のプラズマ 1：地球近傍

未解明の物質 (ダークマター) を除くと、宇宙空間に存在する物質の 90 % 以上はプラズマの状態にあると言われています ( 例えば Gurnett & Bhattacharjee, 2005 の第 1 章; Goedbloed et al., 2019 の 1.1 節)。また、宇宙には磁場も普遍的に存在します。望遠鏡で観測される数々の現象には、しばしば磁場とプラズマの相互作用が重要な役割を果たしていると考えられています。この宇宙を考える際には、プラズマの理解が欠かせません。

既に述べたように、太陽はプラズマの塊です。その結果として起きる現象はこのサイトの他の記事でたくさん紹介しています。その他、プラズマ物理学や 磁気流体力学 脚注 [磁気流体力学]：液体や十分に濃い気体の速度、温度、圧力や密度などの時間発展を計算するための理論を流体力学と言います。特に、プラズマのような電気を通す流体を記述するために、流体力学と電磁気学を融合させた理論を磁気流体力学 (MHD) と言います。 を用いた研究がなされている系を、ほんの一例ですが、紹介します。

電離圏

地上の大気は中性粒子 (\(\text{N}_2\) と \(\text{O}_2\)) から成る中性気体であり、プラズマではありません。これは温度が低く、密度が高いからです。一方で、地球の周りの宇宙空間ではプラズマが主役になります。これは反対に、温度が高く、密度が低いからです。

この意味で「大気」と「宇宙」の境界にあたるのが電離圏 (ionosphere) です。これは高度 60 から 800 km 程度の層に存在しています。参考までに、エベレストの高さは 8.8 km、雲のできる高度は数 km から 10 km 程度までです。大気は電離圏で 電離 脚注 [電離]：粒子が電子を手放して電荷を持つようになることを電離と言います。電荷を持った粒子を含む気体をプラズマと言います。一部の粒子のみが電離している状態を部分電離または弱電離と言います。 しており、これより上ではプラズマが場のダイナミクスに深く関わってくる領域になります。因みに、国際宇宙ステーション (ISS) は高度 400 km の電離圏の中を飛んでいます。

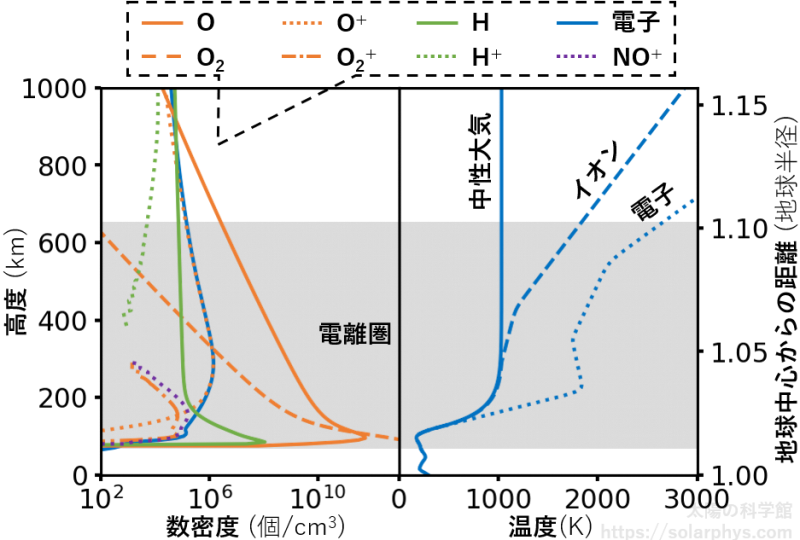
図 7 に各粒子種の数密度 (\(1 \ \text{cm}^3\) あたりに含まれる粒子数) と温度の高度分布を示しました。分布は場所や時間帯、太陽活動度によっても違います。図は昼間の典型的な様子を表したものと捉えてください。

図 7   各粒子種の数密度と温度の高度分布 (地球大気)：左側は各粒子種の数密度 (対数スケール)、右側は温度を表す。中性大気については NRLMSISE-00 ( Picone et al., 2002 )、荷電粒子については IRI-2016 ( Bilitza, 2018 ) の標準モデルを示した。数密度や温度の分布は太陽から降り注ぐ紫外線や X 線の量に依存するため、昼夜によっても異なるほか、太陽活動の影響も受ける。ここで示したのは 2015 年 1 月 1 日の正午、緯度 30 度を想定した値である。

昼間、太陽光が地球大気に降り注ぐと、その中の 紫外線 脚注 [紫外線]：電磁波 (光) のうち、波長が大体 10 nm から 380 nm の領域のものを紫外線と言います。波長 10 nm 付近 (極端紫外線) にある輝線はしばしばコロナの観測に用いられます。紫外線は地球大気に吸収されるので、宇宙からの観測が必要です。 や X 線 脚注 [X 線]：電磁波 (光) のうち、波長が大体 0.01 nm から 10 nm の領域のものを X 線と言います。光子のエネルギーに換算すると、大体 100 eV から 100 keV の領域です。特に、波長 1 nm から 10 nm 程度の光 (軟 X 線) はコロナで発せられ、波長 0.1 nm 以下の光 (硬 X 線) は高エネルギー粒子の加減速によって発せられます。X 線は地球大気に吸収されるので、宇宙からの観測が必要です。 が例えば \(\text{O}_2\) に衝突することで、\(\text{O}_2^+\) や \(\text{O}^+\)、\(\text{O}\)、電子を発生させます。すると、これらの粒子が更に反応を起こすことで、大気中には様々な粒子種が存在するようになります ( 例えば Fox, 2015 )。

それらの反応の起こりやすさは大気の密度などによって変化するため、図 7 の左のように、高度によって異なる種類の荷電粒子が存在します。このあたりの詳細は記事「電離圏：宇宙への入り口」で説明します。

様々な反応によって荷電粒子と共に生成される \(\text{O}\) 原子は、例えば波長 557.7 nm (緑色) や 630.0 nm (赤色) の光を発します ( 例えば Solomon, 2017 )。他の粒子種もそれぞれ固有の色を発します。このため、電離圏を含む高層大気は様々な色に光って見えます ( 図 8 )。これは大気光 (airglow) と呼ばれます。

図 8   国際宇宙ステーション (ISS) によって 可視光 脚注 [可視光]：電磁波 (光) のうち、波長が大体 380 nm から 780 nm の領域のものを可視光と言います。人間の目が感じることのできる領域です。 で捉えられた地球 (夜側)：中東の街灯りの上に大気光が光っている。提供 NASA. Goddard Space Flight Center のサイトで公開されている画像。

図 7 の上端付近の高度では、電子や \(\text{O}^+\)、水から発生した \(\text{H}^+\) などが荷電粒子の中で主成分を占めるようになっています。図 7 の右に示したように、これらの粒子は中性大気より高い温度を持ち、また電子は軽いため、重力の影響が少なく、より高高度に進出することができます。

地球磁気圏

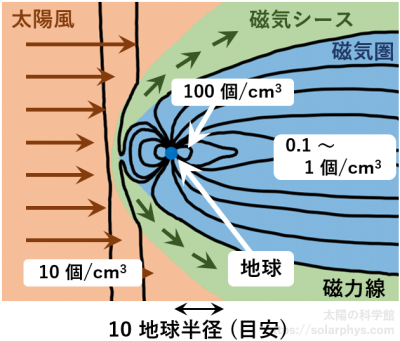
記事「太陽風：常に噴き出すスプリンクラー」で説明しているように、太陽コロナからは常に太陽風と呼ばれるプラズマ (陽子や電子、ヘリウムイオンの集団) が外側に噴き出しており、地球の周りの惑星間空間も満たしています ( 図 9 のオレンジ色 )。

図 9   地球磁気圏の模式図：プラズマの数密度の値は Borovsky & Valdivia (2018) を参考にした。

地球は地磁気と呼ばれる磁場を持っています。地磁気の 磁力線 脚注 [磁力線]：各場所での磁場の向きを繋げた曲線を磁力線と言います。理想的には磁力線の密集度がその場所での磁場の強さ (単位 T, テスラ) を表しますが、実際の図では特徴的な磁力線だけを間引いて描くため、この限りではありません。磁力線が分裂したり合流したりすることはありません。電気を通すプラズマでは磁力線は物質に凍結している (物質は磁力線に垂直な方向に動くことができない) ので、磁力線の動きはその場所でのプラズマ (物質) の動きを表します。 は南半球から出ていて、ループを描いて北半球に突き刺さっています。プラズマと磁場の記事で説明しますが、プラズマは磁力線と垂直な方向には動きにくいという性質を持ちます。このため、太陽風に吹き付けられることで地磁気の磁力線がなびくと共に、太陽風は向きを変えられます。こうして、地球の周りには、地磁気という「傘」によって太陽風から守られた空間ができています ( 図 9 の青色 )。これを磁気圏 (magnetosphere) と言います。磁気圏は太陽と反対方向に長い尾を持つような形状になっています。

磁気圏の各場所には多様な温度、密度のプラズマ (電子と陽イオンの集団) が存在しています ( 例えば Borovsky & Valdivia, 2018 )。地磁気が防ぎきれずに磁気圏に入り込んでしまった太陽風由来のプラズマと、上述した電離圏から供給されるプラズマです。詳しくは記事「地磁気：太陽風から地球を守る壁」で説明します。

これらのプラズマと磁場の相互作用の結果、磁気圏には様々なタイプの電流が存在し、またプラズマの流れもあります。太陽風や記事「CME：噴出するプラズマの雲」で説明している ICME (惑星間空間擾乱) が地球に到来した際に、磁気圏がどのように応答して社会に影響を及ぼすのかを知るためには、それらの現象をひとつひとつ理解していく必要があります。

宇宙のプラズマ 2：太陽系

木星型惑星

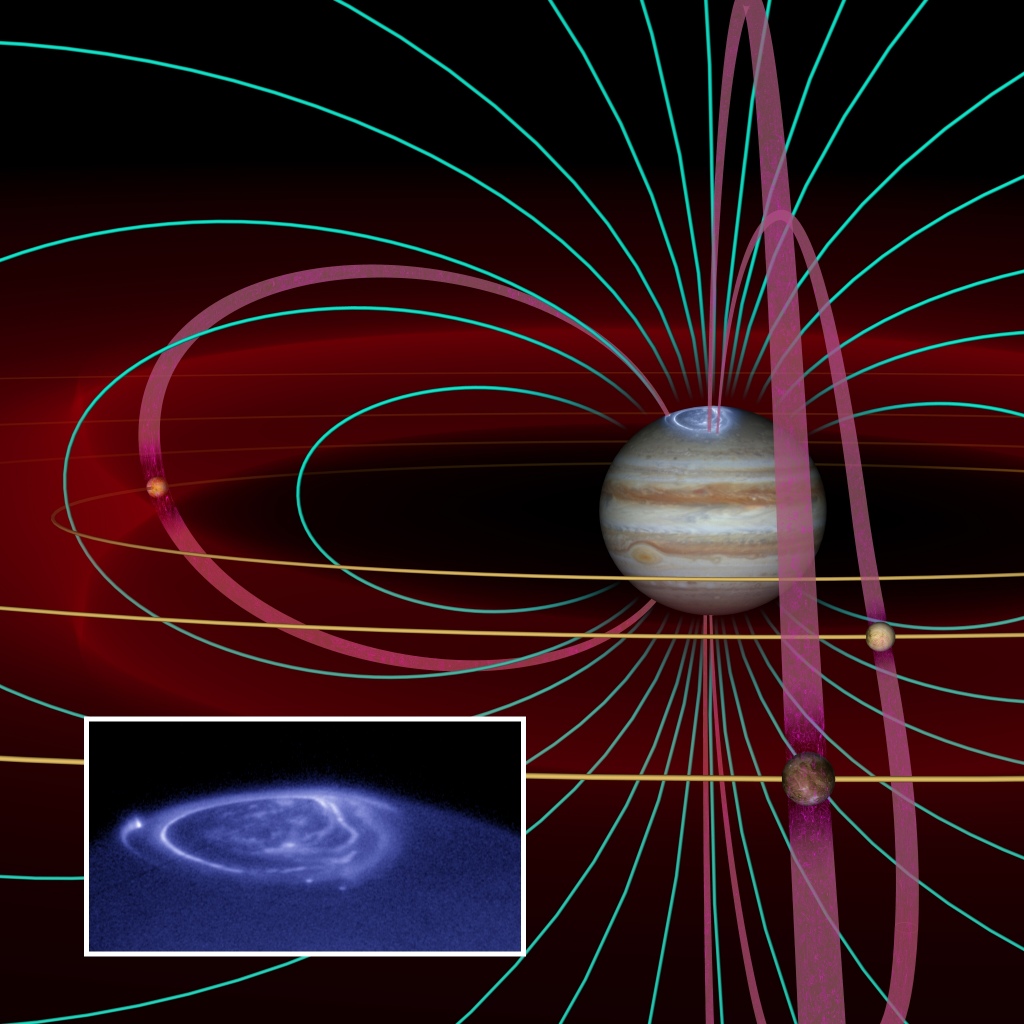
木星や土星は地磁気と同じように固有の磁場を持ち、磁気圏を形成しています。特に木星 ( 図 10 ) は太陽系の惑星の中でいちばん強い磁場を持ちます ( 表面の強い部分で 2 mT 脚注 [テスラ]：磁場の強さを表す単位です。理想的には磁力線の密集度に相当しますが、実際の図では特徴的な磁力線だけを間引いて描くため、この限りではありません。磁場の強さの単位には \(\text{G}\) (ガウス) が使われることもあり、\(1 \ \text{G}=10^{-4} \ \text{T}\) です。 程度; Connerney et al., 2018 )。

図 10   探査機 Juno が可視光で捉えた木星大気：木星大気では緯度によって西か東の異なる向きに強い風が吹いている。それに伴って縞模様やたくさんの渦が作られている。Juno の重力観測結果から、この風は深さ 3000 km ( = 木星半径の 0.04 倍、ほとんど表面) まで存在していて、それ以上の深さには存在しないことが分かってきた ( Kaspi et al., 2020 )。提供 NASA / SwRI / MSSS / Tanya Oleksuik © CC BY-NC-SA 3.0 . JunoCam が捉えた画像は こちらのサイト で公開されている。

木星や土星は磁気圏の中に衛星を持っています。例えば木星の衛星イオは火山活動をしており、それによって放出された酸素や硫黄を起源とするプラズマが、土星の輪のような環状に磁気圏を満たしています。このプラズマは木星の 磁力線 脚注 [磁力線]：各場所での磁場の向きを繋げた曲線を磁力線と言います。理想的には磁力線の密集度がその場所での磁場の強さ (単位 T, テスラ) を表しますが、実際の図では特徴的な磁力線だけを間引いて描くため、この限りではありません。磁力線が分裂したり合流したりすることはありません。電気を通すプラズマでは磁力線は物質に凍結している (物質は磁力線に垂直な方向に動くことができない) ので、磁力線の動きはその場所でのプラズマ (物質) の動きを表します。 に対して大きく動けないので、木星の自転 (周期 10 時間) と共に周りを回っています。このことが木星磁気圏に様々な現象をもたらします。

そのひとつはオーロラです ( 図 11 ) 。木星の極域でも地球と同じようにオーロラが観測されますが、地球とは違う機構によって発生していると考えられています。木星の磁気圏とオーロラについて詳しくは、例えば Bagenal (2007) を読んでください。

図 11   木星のオーロラ：ボタンを押すと説明の表示を切り替えられる。 観測衛星 Hubble Space Telescope が 紫外線 脚注 [紫外線]：電磁波 (光) のうち、波長が大体 10 nm から 380 nm の領域のものを紫外線と言います。波長 10 nm 付近 (極端紫外線) にある輝線はしばしばコロナの観測に用いられます。紫外線は地球大気に吸収されるので、宇宙からの観測が必要です。 で捉えた木星の極域。大気でオーロラが光っている。提供：NASA, ESA & John T. Clarke (Univ. of Michigan). Hubble のサイト (ESA) で公開されている画像。

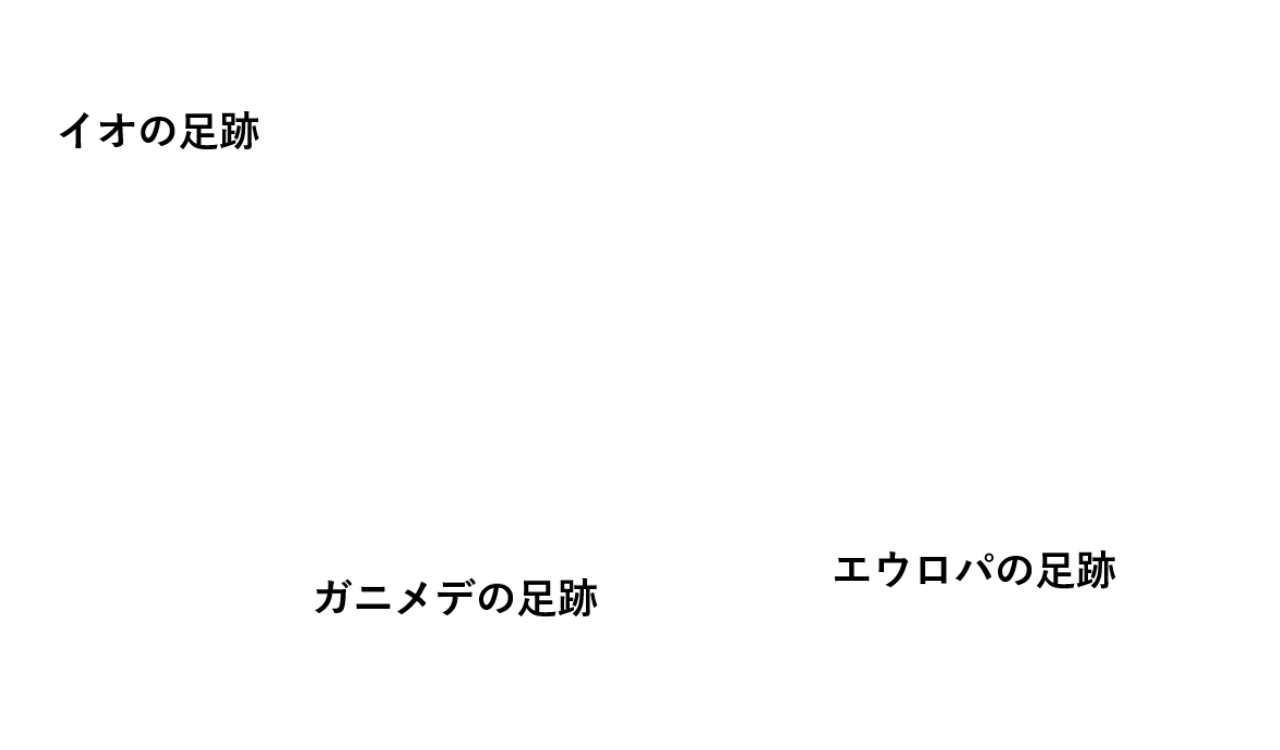
図 11 に写っているオーロラは複数の構造を持ちます。例えば面白い構造として、矢印で示した点状の光は、木星が持つ衛星の足跡を表します。図 12 に示したように、木星の極域から伸びる磁力線の中で、各々の衛星と繋がっているもののふもとが点状に光っています。

図 12   点状のオーロラと各衛星を繋ぐ磁力線の想像図：提供 NASA/John Spencer, Lowell Observatory and John Clarke, Boston University. NASA のサイト で公開されている画像。

記事「基本構造：何からできているのか？」で説明しているように、太陽内部の構造 (密度や温度など) は数 % の精度で分かっています。それに比べて、木星や土星のような惑星の内部構造はまだよく分かっていない部分が多いです ( 例えば Helled et al., 2020 )。この問題を難しくしている要因のひとつは、これらの惑星が液体のような状態にあるということです。

上述したように、木星や土星は地球と同じような形 (南北方向の双極子型) の磁場を持ちます。このことから、木星型惑星の中でも地球や太陽と同じように (具体的な様式は異なりますが) ダイナモ機構が働いていると考えられています ( 詳しくは Wicht et al., 2018 )。ダイナモ機構とは、電気を通す流体の流れによって磁場が作り出されるのではないかという説です。地球の場合は外核 (融解した鉄とニッケル)、太陽の場合は 対流層 脚注 [対流層]：太陽半径を \(R_\odot =\) 約 70 万 km としたとき、\(0.7 R_\odot \)から表面 (\(1 R_\odot\)) までの領域を指します。この領域では主に熱対流によってエネルギーが外側へと運ばれます。 でこの機構が働いていると考えられています。つまり、木星型惑星の内部も電気を通しやすい状態になっていることが強く期待されます。

木星や土星は太陽と同じように、水素とヘリウムが主成分です。しかし、これらの惑星は太陽に比べて温度は格段に低いけれども密度はそこまで低くない、言い換えると、温度のわりに密度が高い状態にあります。このため、これらの元素は太陽と同じように電離した気体の状態にはなり得ず、代わりに金属化した液体のような状態で存在していると考えられます ( 図 13 )。

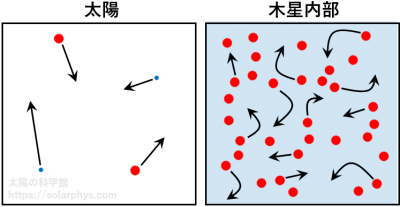
図 13   太陽と木星内部の水素状態の対比：赤色は陽子、青色は電子を想定して描かれている。

狭義には、気体のような状態、つまり粒子たちが周りの粒子に強く束縛されることなく自由に飛び交っている状態をプラズマと言います。しかし、木星内部のように、粒子たちが周りの粒子と強い クーロン力 脚注 [クーロン力]：同じ符号の電荷を持った粒子の間には、互いに離れようとする力が働き、逆符号の電荷を持った粒子間には近づこうとする力が働きます。これをクーロン力と言います。クーロン力は粒子間の距離の 2 乗に反比例します。 で結ばれながら、全体としては流動的に振舞う状態を強結合プラズマ (strongly coupled plasma) と言うことがあります。それに対して狭義のプラズマは弱結合プラズマ (weakly coupled plasma) と呼ばれます。

木星内部の状態を詳細に議論するためには状態方程式を計算しなければなりません。状態方程式とは、物質の圧力と密度、温度の間の関係です。太陽の場合はたくさんの粒子の統計的な性質を扱う理論 (統計力学) によって良い精度で計算されます ( 例えば Däppen, 1993 )。

木星内部の状態方程式の場合は、統計力学によって良い精度の計算ができないため、たくさんの粒子についてのシュレディンガー方程式 (量子力学) に何らかの単純化を施して解くことで、電子の運動を逐一追う手法 (第一原理計算, ab-initio calculation) が取られます。これはコンピュータの高速化によって可能になってきた手法ですが、施す単純化に結果が依存することもしばしばあります ( Helled et al., 2020 )。この不確かさが木星内部の状態推定を難しくする一因です。

2016 年に木星の周回軌道に投入された NASA の探査機 Juno は、これまでにない精度で木星の重力を測定しています。観測された重力の球対称からのずれの情報から、木星内部の状態についての知見が得られます。具体的には、上述の方法で計算された状態方程式を組み込んだ 流体力学 脚注 [流体力学]：液体や十分に濃い気体の速度、温度、圧力や密度などの時間発展を計算するための理論を流体力学と言います。 的モデルを用いて木星内部の状態と観測されるはずの重力を計算し、実際の観測結果と比較します ( 例えば Helled et al., 2020; Wicht et al., 2018 )。

そのような研究の結果、現在推測されている木星内部の状態を 図 14 に示します。図には 2 つの可能性が描かれています。外側の層では水素は電気を通さない液体で存在していますが、内側に行くと、電気を通す液体に変化していきます。

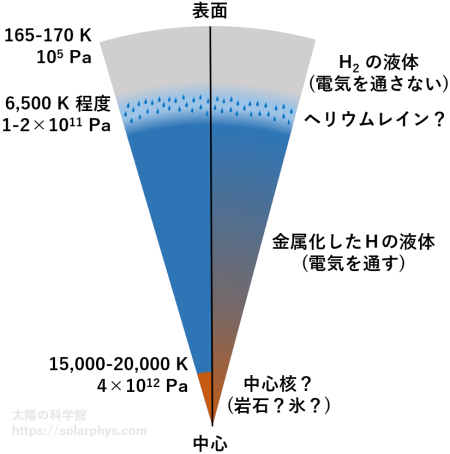
図 14   現在考えられている木星の内部構造の可能性：Helled et al. (2020) の Fig. 5 を参考にした。

両者の境界の 0.8 木星半径程度の領域では、水素とヘリウムが混合状態で存在できない可能性があります。まるで水と油のように分離し、水素の中をより重いヘリウムが雨のように降り注いでいるかもしれません。この現象はヘリウムレイン (helium rain) と呼ばれます。

木星は重元素 (水素やヘリウム以外の元素) を多く含んでいるので、中心には岩石か氷でできた核が存在しているかもしれません。しかし、Juno の観測結果を踏まえた近年の研究では、核と金属水素の境界ははっきりしておらず、中心に行くほど連続的に重い元素の含有率が増えていくような構造になっているかもしれないと考えられるようになってきました ( 詳しくは Helled et al., 2020 )。

太陽圏

太陽風は太陽付近で 400 - 800 km/s 程度まで加速された後、その速さを保ったまま海王星の軌道 ( = 30 au 脚注 [天文単位 (au)]：距離の単位です。1 au = 1 億 5000 万 km は地球と太陽の間の平均的な距離です。 1 au = 215 太陽半径であり、1 光年 = 63,000 au です。他に、地球と月の間の距離は 0.0026 au、海王星の軌道半径は 30 au 程度です。 ) よりも遠くまで放射状に吹いています ( 図 15 の青色 )。

高速の太陽風はどこまでも吹いているわけではなく、太陽から 90 au 程度の距離で流れの淀みにぶつかり、急激に速度を落とします。この球状の面を終端衝撃波, termination shock, 図 15 の青色と緑色の境界 ) と言います。

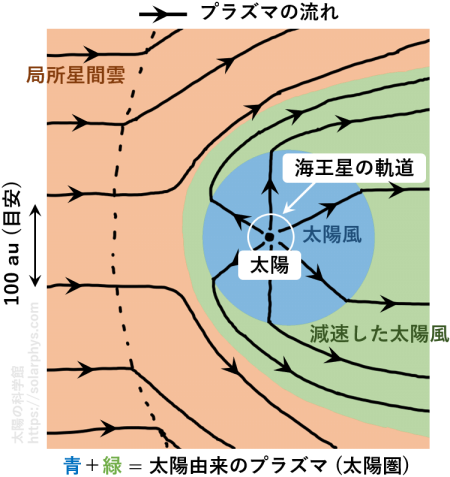
図 15   太陽圏の模式図：Zank (2015) の Figure 1 を参考にした。

太陽は周りを取り巻く局所星間雲 (local interstellar medium) と呼ばれる気体の塊に対して 25 km/s 程度の相対運動をしています。つまり、太陽視点では局所星間雲がその程度の速さで吹き付けています ( 図 15 のオレンジ色 )。これは部分電離したプラズマ (\(\text{H}\), \(\text{H}^+\), 電子などの集団) です。

局所星間雲と減速した太陽風が混ざり合う境界 (図のオレンジ色と緑色の境界) を太陽圏界面 (heliopause) と言います。そして、太陽由来の物質と局所星間雲の相互作用の結果生まれる一連の構造を太陽圏 (heliosphere) と言います。

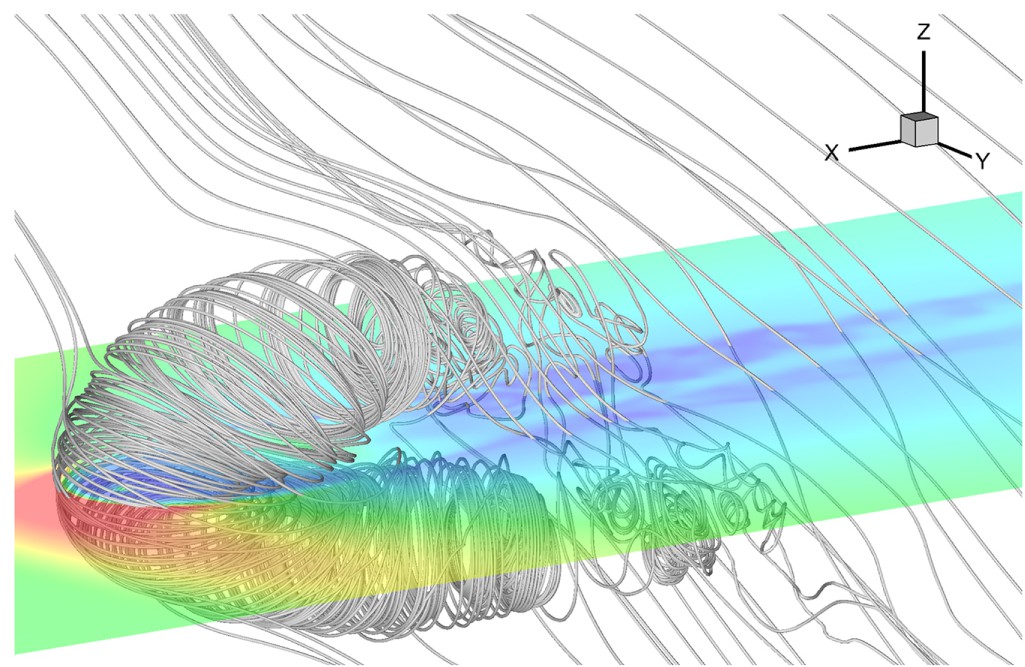
記事「磁場の構造 1：コロナや惑星間空間の磁場モデル」で説明しているように、太陽圏には太陽自転の結果としてスパイラル状の 磁力線 脚注 [磁力線]：各場所での磁場の向きを繋げた曲線を磁力線と言います。理想的には磁力線の密集度がその場所での磁場の強さ (単位 T, テスラ) を表しますが、実際の図では特徴的な磁力線だけを間引いて描くため、この限りではありません。磁力線が分裂したり合流したりすることはありません。電気を通すプラズマでは磁力線は物質に凍結している (物質は磁力線に垂直な方向に動くことができない) ので、磁力線の動きはその場所でのプラズマ (物質) の動きを表します。 (パーカースパイラル) が存在しています。一方で、局所星間雲も磁場を持っています。太陽圏界面では両者が 図 16 のように絡み合い、パーカースパイラルは下流へなびいているかもしれません。

図 16   太陽圏と局所星間雲の相互作用のシミュレーション例：曲線は磁力線を表し、切断面に描かれた色はプラズマの密度を表す。Pogorelov et al. (2015) の Figure 1 より引用。米国天文学会 の許可を得て掲載。© AAS. Reproduced with permission.

NASA の探査機ボイジャー 1 号は 2004 年に太陽から 94 au の距離で終端衝撃波を横切りました。それに続き、2007 年にボイジャー 2 号が 84 au の距離で終端衝撃波を横切りました。この 2 つの探査機はそれぞれ違う方向に向かって太陽から遠ざかり続けると共に、今も太陽圏界面付近の磁場やプラズマの性質を測定しています。

ボイジャーのその場観測や 2008 年に打ち上げられた NASA の観測衛星 IBEX による高速中性粒子 (ENA) の観測データなどから、太陽圏界面付近の様子はそれまで考えられていたよりも複雑であることが分かってきました ( 詳しくは Pogorelov et al., 2017; Opher, 2016 )。

前述したように、プラズマ (荷電粒子) は基本的には磁力線と垂直な方向に動くことができません。一方で、局所星間雲の中性原子 (\(\text{H}\)) は磁場から力を受けないため、磁力線を横切って太陽圏に侵入します。すると、太陽風の \(\text{H}^+\) と電荷を交換する反応を起こします。

\[\text{H}+\text{H}^+\longrightarrow \text{H}^+ + \text{H}\]

この反応で生成された \(\text{H}^+\) の集団は局所星間雲由来のものなので、太陽風とは違う温度を持っています。このような機構が各所で起きることによって、太陽圏や周りの局所星間雲では異なる性質を持った複数の粒子集団が共存しています。このことが問題を難しくしています。

残念ながら太陽圏は外側から見て形を確認することができませんが、夜空に浮かぶ他の恒星が作る恒星圏 (astrosphere) ならば見ることができます。例えば 図 17 はオリオン大星雲 (Orion Nebula) の画像です。オリオン大星雲は地球から見るとオリオン座に位置していて、街灯りの少ない場所ならば肉眼でぼんやりとしたシミのように見えます。

図 17   オリオン大星雲とその中にある LL Ori が作る恒星圏：ボタンを押すと表示を切り替えられる。 (全体) オリオン大星雲の全体像。観測衛星 Hubble Space Telescope とヨーロッパ南天天文台 (ESO, チリ) の 2.2 メートル望遠鏡が複数の波長の光で撮影した画像を色付けして合成したもの。オリオン大星雲が地球から 1500 光年 脚注 [光年]：距離の単位です。1 光年 = \(9.5 \times 10^{15} \ \text{m}\) は光が 1 年間に進むことのできる距離です。太陽と地球の間の距離 (1 au) は \(1.6\times 10^{-5}\) 光年、太陽からいちばん近い恒星であるケンタウルス座の α 星までの距離は 4.3 光年、夜空に最も明るく輝く恒星であるおおいぬ座のシリウスまでの距離は 8.6 光年、太陽のある天の川銀河の直径は 10 万光年ほどです。 太陽近隣の地図：平面上に投影したもの。距離の目盛の単位は光年。提供 NASA/Goddard/Adler/U. 離れているとすると、画像の端から端までが 13 光年の距離に相当する。提供 NASA, ESA, M. Robberto (Space Telescope Science Institute/ESA) and the Hubble Space Telescope Orion Treasury Project Team. Hubble のサイト で公開されている画像。 (拡大) オリオン大星雲の中にある若い恒星 LL Ori が作る恒星圏の様子。観測衛星 Hubble Space Telescope が複数の波長の光で撮影した画像を色付けして合成したもの。オリオン大星雲が地球から 1500 光年 脚注 [光年]：距離の単位です。1 光年 = \(9.5 \times 10^{15} \ \text{m}\) は光が 1 年間に進むことのできる距離です。太陽と地球の間の距離 (1 au) は \(1.6\times 10^{-5}\) 光年、太陽からいちばん近い恒星であるケンタウルス座の α 星までの距離は 4.3 光年、夜空に最も明るく輝く恒星であるおおいぬ座のシリウスまでの距離は 8.6 光年、太陽のある天の川銀河の直径は 10 万光年ほどです。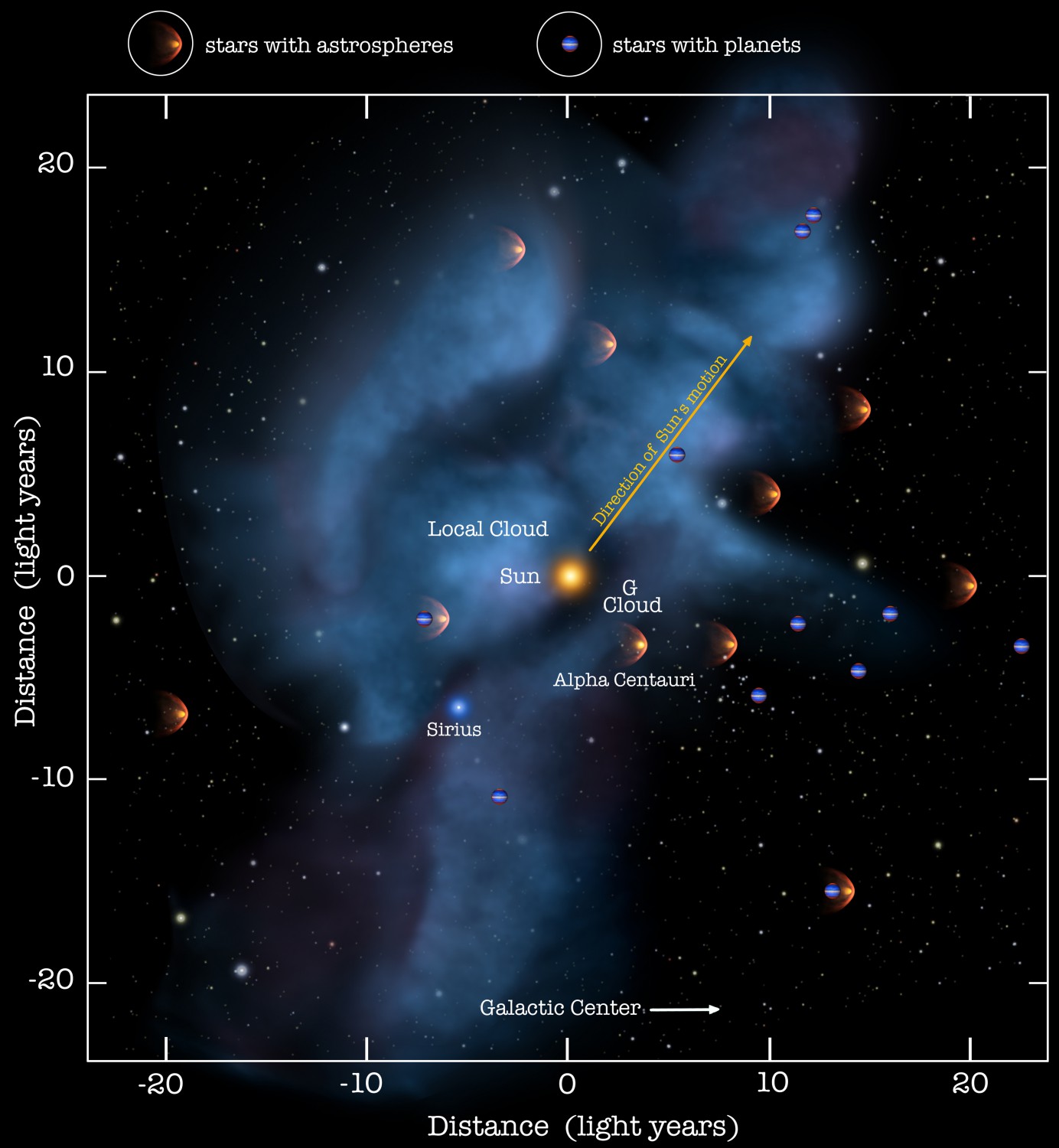 太陽近隣の地図：平面上に投影したもの。距離の目盛の単位は光年。提供 NASA/Goddard/Adler/U. 離れているとすると、画像の端から端までが 0.8 光年の距離に相当する。提供 NASA and The Hubble Heritage Team (STScI/AURA); C. R. O'Dell (Vanderbilt University). Hubble のサイト で公開されている画像。

図 17 の拡大画像はオリオン大星雲の中にある LL Ori という恒星が作りだす恒星圏の様子です。LL Ori が放つ恒星風 (stellar wind) と星雲の気体との間に弧状の衝撃波ができている様子が写っています。これはバウショック (bow shock) と呼ばれます。船の進行方向にできる船首波 (bow wave) に似た現象です。磁気圏も太陽方向にバウショックを持ちます ( 図 9 の オレンジ色と緑色の境界)。太陽圏も持っている可能性があります ( 図 15 の黒い点線 )。

宇宙のプラズマ 3：彼方

パルサー星雲

図 18 は比較的有名な天体であるかに星雲 (Crab Nebula) です。かに星雲は地球から見ると、おうし座に位置しています。おうし座は冬の大六角形を構成するアルデバランを有する星座です。図では 5 種類の波長の光で撮影された同じ領域の画像と、それらを 1 枚に合成した画像が示されています。

図 18   様々な波長の光で見たかに星雲：ボタンを押すと表示を切り替えられる。 (合成) 以下の 5 枚の画像を合成したもの。(X 線) 観測衛星 Chandra が X 線 脚注 [X 線]：電磁波 (光) のうち、波長が大体 0.01 nm から 10 nm の領域のものを X 線と言います。光子のエネルギーに換算すると、大体 100 eV から 100 keV の領域です。特に、波長 1 nm から 10 nm 程度の光 (軟 X 線) はコロナで発せられ、波長 0.1 nm 以下の光 (硬 X 線) は高エネルギー粒子の加減速によって発せられます。X 線は地球大気に吸収されるので、宇宙からの観測が必要です。 で観測した画像。提供 NASA/CXC/SAO. (紫外線) 観測衛星 XMM-Newton が 紫外線 脚注 [紫外線]：電磁波 (光) のうち、波長が大体 10 nm から 380 nm の領域のものを紫外線と言います。波長 10 nm 付近 (極端紫外線) にある輝線はしばしばコロナの観測に用いられます。紫外線は地球大気に吸収されるので、宇宙からの観測が必要です。 で観測した画像。提供 ESA/XMM-Newton. (可視光) 観測衛星 Hubble Space Telescope が 可視光 脚注 [可視光]：電磁波 (光) のうち、波長が大体 380 nm から 780 nm の領域のものを可視光と言います。人間の目が感じることのできる領域です。 (吸収線) で観測した画像。提供 NASA/STScI. (赤外線) 観測衛星 Spitzer Space Telescope が 赤外線 脚注 [赤外線]：電磁波 (光) のうち、波長が大体 780 nm から 0.1 mm の領域のものを赤外線と言います。波長帯によっては地球大気に吸収されます。 で観測した画像。提供 NASA/JPL/Caltech. (電波) 電波望遠鏡 Karl G. Jansky Very Large Array (VLA) が 電波 脚注 [電波]：電磁波 (光) のうち、波長が大体 0.1 mm より大きい領域のものを電波と言います。このうち、地球大気に吸収・反射されずに地上で観測できる領域は波長 1 mm から 10 m 程度 (周波数に換算すると 30 MHz から 300 GHz) です。多彩な物理機構によって発せられたものが観測されます。 で観測した画像。提供 NSF/NRAO/VLA. (全体) かに星雲が地球から 6500 光年 脚注 [光年]：距離の単位です。1 光年 = \(9.5 \times 10^{15} \ \text{m}\) は光が 1 年間に進むことのできる距離です。太陽と地球の間の距離 (1 au) は \(1.6\times 10^{-5}\) 光年、太陽からいちばん近い恒星であるケンタウルス座の α 星までの距離は 4.3 光年、夜空に最も明るく輝く恒星であるおおいぬ座のシリウスまでの距離は 8.6 光年、太陽のある天の川銀河の直径は 10 万光年ほどです。 太陽近隣の地図：平面上に投影したもの。距離の目盛の単位は光年。提供 NASA/Goddard/Adler/U. 離れた場所にあるとすると、画像の端から端までがおよそ 10 光年の距離に相当する。Chandra のサイト (ハーバード大学) で公開されている画像。

かに星雲はパルサー星雲 (pulsar wind nebula) と呼ばれる種類の天体です。 X 線 脚注 [X 線]：電磁波 (光) のうち、波長が大体 0.01 nm から 10 nm の領域のものを X 線と言います。光子のエネルギーに換算すると、大体 100 eV から 100 keV の領域です。特に、波長 1 nm から 10 nm 程度の光 (軟 X 線) はコロナで発せられ、波長 0.1 nm 以下の光 (硬 X 線) は高エネルギー粒子の加減速によって発せられます。X 線は地球大気に吸収されるので、宇宙からの観測が必要です。 や 紫外線 脚注 [紫外線]：電磁波 (光) のうち、波長が大体 10 nm から 380 nm の領域のものを紫外線と言います。波長 10 nm 付近 (極端紫外線) にある輝線はしばしばコロナの観測に用いられます。紫外線は地球大気に吸収されるので、宇宙からの観測が必要です。 の画像では星雲の中心に点状の光が見えます。これは中性子星 (neutron star) という種類の星であり、かに星雲の生みの親です。中性子星は太陽と同程度の質量が半径 10 km 程度 (山手線くらい) にまとまった超高密度の天体です。

1054 年に、今のかに星雲の場所にあった恒星が燃え尽き、超新星爆発 (supernova explosion) を起こしました。このときには地球でも非常に明るく見えたようであり、中国の古文書には昼間でも金星のように見ることができたと記録されています ( 例えば Blandford & Bühler, 2017 )。また、藤原定家の『明月記』にも、木星のように輝いたという記録があるようです ( 臼井, 2004 )。

元の星 (親星) の大部分は爆発で吹き飛び、周りに広がっていきます ( 図 19 の上段 )。同時に親星の中心核は収縮し、先ほど述べた中性子星としてその場に残ります。こうして、中性子星の周りは電子と水素イオンを主成分とするプラズマ (超新星残骸, supernova remnant) で満たされます。かに星雲の中性子星は 0.03 秒の周期で激しく自転しており、パルス状の光を発しています。そのような中性子星は特にパルサーと呼ばれます。

図 19   かに星雲の構造

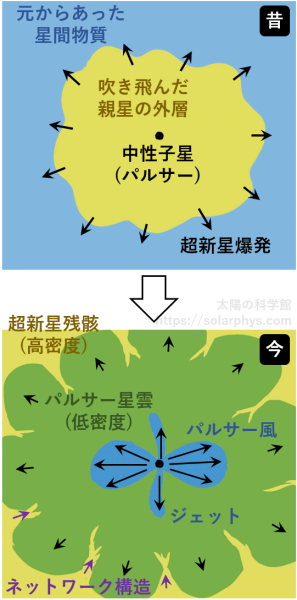
太陽は太陽風を周りに噴き出していますが、パルサーはパルサー風と呼ばれるほとんど光速のプラズマの風を、主に赤道方向に吹き出しています ( 図 19 の下段の青色 )。これは中性子星の表面付近で対生成された電子と陽電子 (電子の反物質、正の電荷を持つ) を主成分とするプラズマだと考えられています ( 例えば Pétri, 2016 )。

噴き出したパルサー風はやがて終端衝撃波を形成して速度を弱めますが、なお外向きに流れることで周りの超新星残骸を侵食し、パルサー星雲を作り出します (図の下段の緑色)。自転軸方向にはジェットと呼ばれる流れも発生しています。図 18 の X 線画像では左下に伸びたジェットを確認できます。また、ジェットと垂直な方向にリング状の構造もいくつか見えますが、そのうちのいちばん内側のリングが終端衝撃波に相当すると考えられています。

パルサー星雲とその周りを取り囲む超新星残骸では、後者の方が密度が高いです。これは軽い気体の上に重い気体が乗っているようなものなので、超新星残骸は根を伸ばすようにして中性子星に向かって落ち込むだろうと考えられます ( 図 19 の下段の紫色 )。これが 図 18 の可視光の画像で顕著に見えているネットワーク状の構造であると考える研究者もいます ( Porth et al., 2014a )。

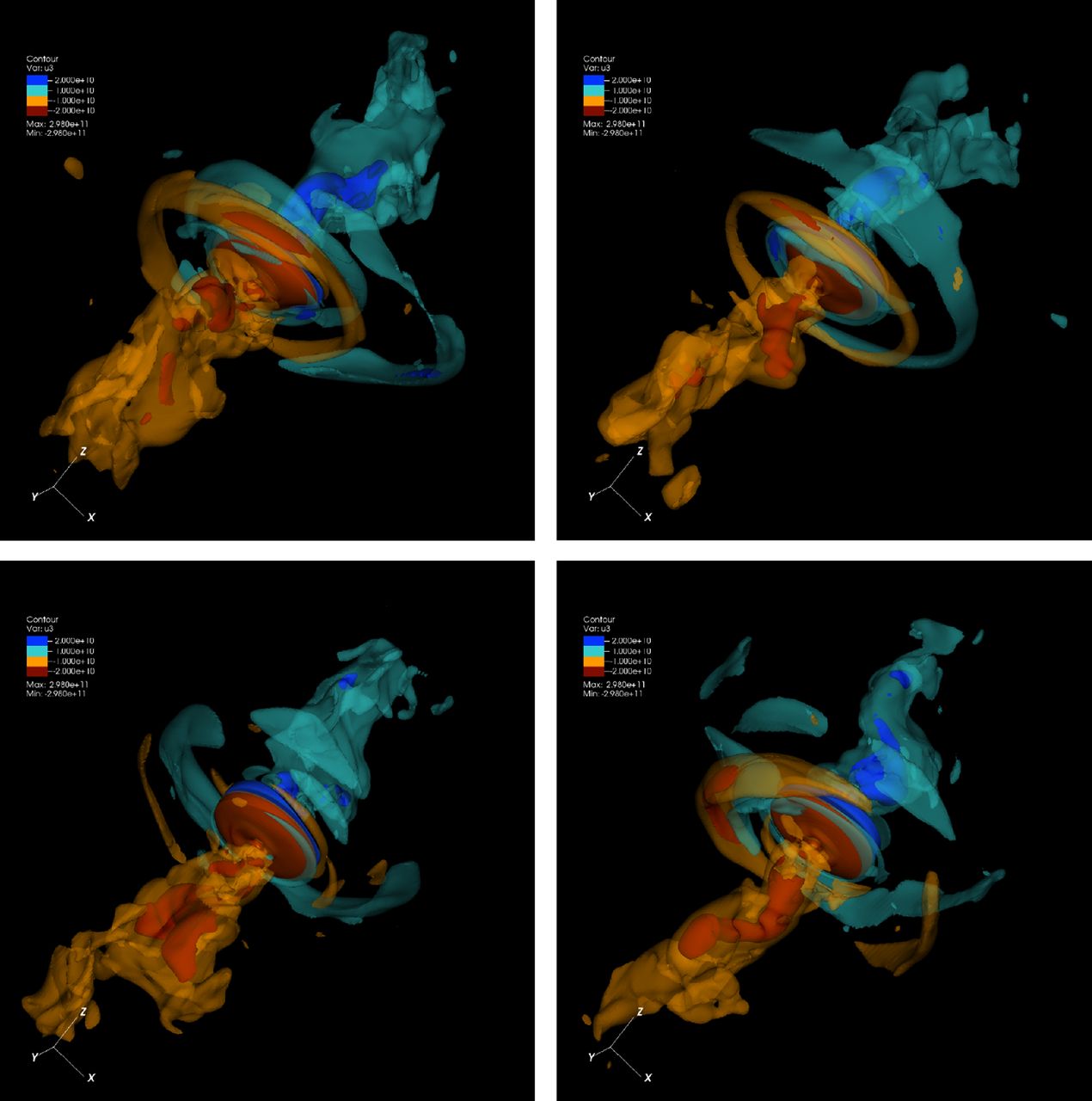
パルサー風やジェットは光速に近い速度を持つため、かに星雲の研究には特殊相対性理論を考慮した 磁気流体力学 脚注 [磁気流体力学]：液体や十分に濃い気体の速度、温度、圧力や密度などの時間発展を計算するための理論を流体力学と言います。特に、プラズマのような電気を通す流体を記述するために、流体力学と電磁気学を融合させた理論を磁気流体力学 (MHD) と言います。 方程式系が用いられます。図 20 に示したのはパルサー風とかに星雲の 3 次元シミュレーション結果です。ジェットが再現されています。

図 20   かに星雲のシミュレーション結果：示されている 4 枚の画像はそれぞれ別の瞬間を切り取ったもの。流速の自転軸方向成分 \(u_z\) の等値面が半透明で示されている。赤色、オレンジ色、水色、青色の順に \(u_z = -2c/3, -c/3, c/3, 2c/3\) を表す。ただし、\(c = 3\times 10^8 \ \text{m/s}\) は光速。Porth et al. (2014b) の Figure 15 より引用。

白色矮星

最後に、極端な環境の例をひとつ紹介します。

夜空に輝く天体の中には白色矮星 (white dwarf) と呼ばれる種類の星があります。暗いので肉眼では見えません。例えば、夜空でいちばん明るく輝く恒星であるおおいぬ座のシリウスは連星系をなしています ( 図 21 )。連星とは 2 つの星が互いに互いの周りを回っている状態にあることです。肉眼で明るく見える方の星を特にシリウス A と呼びますが、その相方のシリウス B が白色矮星であることが知られています。

図 21   明るいシリウス A と暗いシリウス B ：真ん中で明るく輝くのがシリウス A。その左下に写っている小さな光源がシリウス B。観測衛星 Hubble Space Telescope によって観測された。シリウスが 8.6 光年 脚注 [光年]：距離の単位です。1 光年 = \(9.5 \times 10^{15} \ \text{m}\) は光が 1 年間に進むことのできる距離です。太陽と地球の間の距離 (1 au) は \(1.6\times 10^{-5}\) 光年、太陽からいちばん近い恒星であるケンタウルス座の α 星までの距離は 4.3 光年、夜空に最も明るく輝く恒星であるおおいぬ座のシリウスまでの距離は 8.6 光年、太陽のある天の川銀河の直径は 10 万光年ほどです。 太陽近隣の地図：平面上に投影したもの。距離の目盛の単位は光年。提供 NASA/Goddard/Adler/U. 離れた場所にあるとすると、2 つの星は前後関係を無視すれば 16 au 離れているように見えていることになる。 提供 NASA, ESA, H. Bond (STScI), and M. Barstow (University of Leicester). Hubble のサイト で公開されている画像。

白色矮星は太陽の 100 億年後の姿です。現在の太陽は中心部で水素を消費してヘリウムを生成する核融合反応が起きています。詳しくは記事「ニュートリノ問題：エネルギー源は何？」で説明しています。

核融合反応によって中心部の水素はどんどん減っていき、およそ 50 億年後に枯渇します。すると、太陽は現在と同じような熱的バランスを保てなくなり、今の 2000 倍以上の光度 (明るさ) を持つ赤色巨星 (red giant) への進化が始まります。

進化が進むと、今度は中心部に増えたヘリウムを消費して炭素や酸素を生成する核融合反応が起き始めます。そして 78 億年後、高密度の中心部だけをその場に残して、外層を全て宇宙空間に放出してしまいます。

このときに残る中心部が白色矮星です。白色矮星はもはや核融合を起こしておらず、ただただ冷えていくだけの星です。つまり、夜空に光る白色矮星は、昔存在していた太陽のような恒星の最期の姿です。太陽や恒星の進化について詳しくは、例えば Christensen-Dalsgaard (2020) や Kippenhahn et al. (2012) を読んでください。

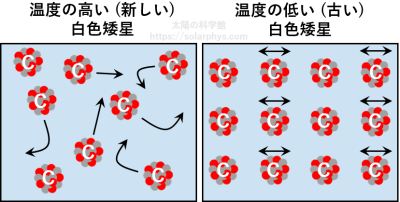
白色矮星は、太陽の 0.6 倍程度の質量が地球程度の大きさにまとまった高密度の星です。白色矮星の大部分は、かつての核融合反応で生成された炭素や酸素から成る強結合プラズマ (液体のような状態) です ( 図 22 の左 )。ただし、冷却が進んだ古い白色矮星の内部は結晶化し、固体になっているかもしれません ( 図 22 の右; 例えば Fontaine et al., 2013 )。

図 22   白色矮星の中心部のイメージ：赤色が陽子、灰色が中性子、青色が電子を想定して描かれている。図は炭素を想定して描いたが、酸素もいくらかの割合で含まれると考えられている。

プラズマとは何か

狭義のプラズマとは、次の 3 つの条件を満たす状態のことを言います ( 例えば Gurnett & Bhattacharjee, 2005 の第 1 章 )。

  1. 電荷を持った粒子の集団である。
  2. 準中性：全体的には中性である。つまり、例えば \(\text{H}^+\) と電子から成るプラズマの場合、\(\text{H}^+\) の数密度と電子の数密度はあらゆる場所でおよそ等しい。
  3. 弱結合：気体のような状態にある。つまり、各々の粒子は基本的に、近隣の粒子から受ける クーロン力 脚注 [クーロン力]：同じ符号の電荷を持った粒子の間には、互いに離れようとする力が働き、逆符号の電荷を持った粒子間には近づこうとする力が働きます。これをクーロン力と言います。クーロン力は粒子間の距離の 2 乗に反比例します。 に強く束縛されることなく、自由に飛び交っている。

準中性 (条件 2) について

プラズマ物理学が対象とする系は 準中性 脚注 [準中性]：プラズマは荷電粒子の集団ですが、基本的には正電荷の数密度と負電荷の数密度はあらゆる場所でおよそ等しく、全体的には中性になっています。これを準中性と言います。 (quasi-neutrality) が保たれています。例えば電子のみの集団が存在したとしたら、それはプラズマとは呼びません。電子があれば、その電荷を打ち消すだけの正電荷 (多くの場合は陽イオン) も存在しなければなりません。自然界では一方の電荷だけが選択的に生成 (損失) することは起きにくく、基本的に準中性が保たれています。

初めに準中性にあったプラズマでは、その後も準中性を保ち続けようとする機構が働きます。例えば \(\text{H}^+\) (陽イオン) と電子から成るプラズマを考えます。図 23 に模式的に描いたように、何らかの原因によって準中性からの乱れが発生し、プラズマの中に陽イオン過多の領域と電子過多の領域ができたとします。

図 23   準中性からの乱れがあった場合に起きる電場

陽イオン過多の領域は全体として正の電荷を持ち、電子過多の領域は負の電荷を持ちます。このとき、両者の間には図のように電場が発生するため、電子過多の領域の電子は電場と反対の向きに加速され、陽イオン過多の領域に移動しようとします。

このようにして、陽イオンと電子の数密度の不一致を和らげようとする機構が働きます。この機構が起きる時間スケール \(\tau\) [秒] は次のように見積もられます。

\begin{align} \tau &= \frac{1}{\omega_\text{pe}} = \sqrt{\frac{\epsilon_0 m_\text{e}}{n_\text{e}e^2}} \\ \text{ただし}, \quad \omega_\text{pe} &: \text{プラズマ周波数} \\ n_\text{e} &: \text{電子の数密度 [個/m}^3\text{]} \\ e &= 1.60 \times 10^{-19} \ \text{C} \\ &: \text{素電荷} \\ \epsilon_0 &= 8.85 \times 10^{-12} \ \text{m}^{-3}\text{kg}^{-1}\text{s}^4\text{A}^2 \\ &: \text{真空の誘電率} \\ m_\text{e} &= 9.11 \times 10^{-31} \ \text{kg} \\ &: \text{電子の質量}\end{align}

補足 A：簡単なモデルで上式を導く

準中性からの乱れが発生した際に荷電粒子の集団がどのように応答するのかを大雑把に見積もるために、次の簡単なモデルを考えます。\(\text{H}^+\) (陽子) と電子の集団を想定します。

図 A1   プラズマ振動の簡単なモデル

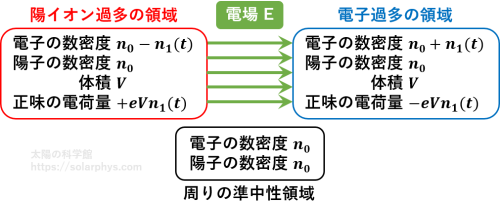
図 A1 のように、初めに電子と陽子の数密度が共に \(n_0\) であり、準中性が保たれていた系において、体積 \(V\) の領域に電子過多が発生したとします。増えた電子の分だけ隣の領域では減っているため、隣の領域では陽イオン過多 (電子不足) になっています。それぞれの領域の正味の電荷量は図に書いた通りです。乱れは小さい (\(|n_1| \ll n_0\)) とします。

温度の記事 で説明しますが、各粒子は 熱運動 脚注 [熱運動]：気体 (プラズマ) を構成する粒子たちの平均速度をその気体の流速と言います。流速と共に移動する観測者から見ても、各粒子たちはそれぞれ勝手な方向に運動しています。これを熱運動と言います。その速度分布の幅が温度です。具体的には、例えば電子の熱運動の速さの平均を \(\overline{v}_\text{e}\) としたとき、電子 1 個の持つ平均的な運動エネルギー \(m_\text{e}\overline{v}_\text{e}^2/2\) が \(k_BT_\text{e}\) に相当します。\(T_\text{e}\) は電子の温度です。ボルツマン定数 \(k_B = 1.38\times 10^{-23} \ \text{J K}^{-1}\) は温度とエネルギーの単位換算のための物理定数です。 によってそれぞれ勝手な向きに運動しています。ここでは熱運動を無視し、各粒子は基本的に静止しているとして議論を進めます。

陽子の質量は電子の質量の 1800 倍あります。準中性からの乱れに対して真っ先に応答するのは軽い電子なので、陽子は終始静止しており、2 つの領域の間に発生した一様電場によって電子だけが加速されると考えます。

電子過多の領域の表面積を \(S\) とします。この表面に対して ガウスの法則 脚注 [(電場についての) ガウスの法則]：あらゆる場所で電場と電荷が従わなければならない関係です。任意の閉曲面を考えたとき、その曲面の内側にある電荷の合計と、表面を貫く電場の曲面全体に渡る合計は図の関係にあります。 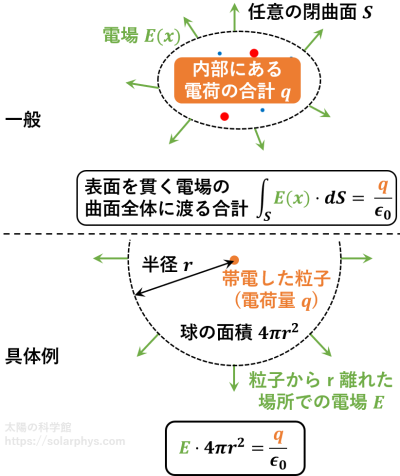を適用することで、発生した電場の大きさ \(E\) は次のように表せます。

\[E = \frac{eVn_1}{\epsilon_0 S} \tag{A1}\]

発生した電場によって、電子過多の領域内の電子は、次の運動方程式に従って一様に加速されると考えます。

\[m_\text{e}\frac{dv}{dt} = eE \tag{A2}\]

\(v\) は電子の速さです。電場に加速された電子が流出することで、領域内の電子の数密度は減っていきます。速さ \(v\) の電子が時間 \(\delta t\) の間に流出する個数は \(n_0Sv\delta t\) と見積もられるので、領域内の電子数の時間変化は次のように書けます。

\[V\frac{dn_1}{dt} = -n_0Sv\]

この式をもう一回時間微分することで、次式を得ます。

\[\frac{d^2n_1}{dt^2} = -\frac{n_0S}{V}\frac{dv}{dt}\]

ここに式 (A1) と式 (A2) を代入することで、次式を得ます。

\[\frac{d^2n_1}{dt^2} = -\frac{n_0e^2}{\epsilon_0m_\text{e}}n_1\]

これは単振動の微分方程式であり、次の解を持ちます。

\begin{align} n_1(t) = n_1&(0)\cos(\omega_\text{pe}t) \\ \text{ただし}, \quad \omega_\text{pe} &= \sqrt{\frac{n_0e^2}{\epsilon_0m_\text{e}}} \\ &: \text{プラズマ周波数}\end{align}

つまり、電子は電場に加速されて流出しますが、慣性を持つため準中性の状態 (\(n_1=0\)) を超えて流出しすぎてしまいます。すると、逆向きの電場が発生して今度は流入が起こり、行き過ぎてまた流出が起き、という繰り返しになります。この現象をプラズマ振動 (plasma oscillation) と言います。

プラズマ振動の周期は桁数としては \(1/\omega_\text{pe}\) です。これより長い時間スケールでゆっくりと準中性からの乱れが起きようとする場合、電子は即座に応答するため、乱れ (プラズマ振動の振幅) は大きくならないと考えられます。

因みに、上のモデルでは熱運動を無視しましたが、この仮定の是非について考えます。温度の記事で説明しますが、電子の熱運動の典型的な速さは次の式で表されます。

\begin{align} \overline{v}_\text{e} &= \sqrt{\frac{k_BT}{m_\text{e}}} \\ \text{ただし}, \quad k_B &= 1.38 \times 10^{-23} \ \text{J K}^{-1} \\ &: \text{ボルツマン定数} \\ T &: \text{温度 [K]} \end{align}

プラズマ振動の典型的な時間スケール \(1/\omega_\text{pe}\) の間に熱運動によって電子が移動する距離は次のように書けます。

\[\lambda_D = \frac{\overline{v}_\text{e}}{\omega_\text{pe}} = \sqrt{\frac{\epsilon_0 k_B T}{n_0e^2}}\]

この \(\lambda_D\) をデバイ長 (Debye length) と言います。デバイ長よりずっと大きな空間スケールでの現象 (乱れ) を考えているならば、プラズマ振動の時間スケールでの熱運動を無視した上のモデルはそこまで悪くないと言えます。

まとめると、デバイ長よりもずっと大きく、プラズマ周波数の逆数よりもずっと遅い現象を対象とする場合は、準中性が保たれていると考えられます。例えば太陽コロナのデバイ長は 1 mm、地球磁気圏を構成するプラズマ圏のデバイ長は 1 m 程度です。

補足の先頭へ

例えば太陽コロナの場合は \(10^{-10}\) 秒、地球磁気圏を構成するプラズマ圏と呼ばれる領域の場合は \(10^{-6}\) 秒程度の短い時間です。普通、興味のある現象はそれよりもずっと長い時間スケールで起きます。電荷のバランスの乱れがあっても電子が即座に対応するため、準中性からのずれは小さいことが期待されます。プラズマが薄いほど \(\tau\) は大きくなります。

弱結合 (条件 3) について

上の節でも述べたように、狭義のプラズマは弱結合の状態にあるものを指します。プラズマは荷電粒子の集団なので、粒子は近隣の粒子から クーロン力 脚注 [クーロン力]：同じ符号の電荷を持った粒子の間には、互いに離れようとする力が働き、逆符号の電荷を持った粒子間には近づこうとする力が働きます。これをクーロン力と言います。クーロン力は粒子間の距離の 2 乗に反比例します。 を受けます。その力によるポテンシャル (位置エネルギー) より各粒子の運動エネルギーが大きい場合、各粒子はクーロン力に強く縛られることなく自由に運動することになります。これが弱結合です。

逆に、各粒子の運動エネルギーがクーロン力のポテンシャルと同じくらいか、それよりも小さい場合、各粒子の運動はクーロン力によって束縛されていることになります。これが強結合です。広義にはこの状態も強結合プラズマと言うのでした。

クーロンポテンシャルと各粒子の運動エネルギーの比を結合係数 \(\Gamma\) と言います (次式)。\(\Gamma \ll 1\) ならば弱結合、\(\Gamma \gtrsim 1\) ならば強結合と言えます。

\begin{align} \Gamma &= \frac{\text{クーロンポテンシャル}}{\text{各粒子の運動エネルギー (熱エネルギー)}} \\ &= 2.7\times 10^{-5}\cdot\frac{Q^2n^{1/3}}{T} \end{align}

\(Q\) は正の荷電粒子の電荷数 (\(\text{H}^+\) なら 1) です。数密度 \(n\) は単位 \(\text{/m}^3\) で、温度 \(T\) は単位 \(\text{K}\) で表したときの値を代入します。熱くて希薄な系が弱結合プラズマになります。例えば太陽コロナは \(10^{-6}\) 程度です。太陽内部では表面近くがいちばん大きく、\(\Gamma \approx 0.3\) 程度になります。0.8 太陽半径くらいの深さでは \(\Gamma \approx 0.07\) 程度です。

一方、温度のわりに密度が高い系が強結合プラズマになります。木星内部は \(\Gamma \approx 50\) ほどです。また、上式は \(Q^2\) に比例しており、正電荷の価数が多い系も強結合になりやすいです。

補足 B：上式の詳細

結合係数 \(\Gamma\) は粒子間にはたらく平均的なクーロンポテンシャルの大きさ \(\phi_C\) と各粒子の平均的な運動エネルギーの比として定義されます。

正の電荷 \(+Qe\) を持つ粒子間にはたらくクーロンポテンシャルを見積もります。粒子間の平均距離を \(a\) とすると、\(\phi_C\) は次のように表されます。

\begin{align} \phi_C &= \frac{Q^2e^2}{4\pi\epsilon_0 a} \end{align}

平均距離 \(a\) は、粒子 1 個が占める球状の体積を考えることで、数密度 \(n\) との間に次の関係があるものとして見積もることができます。

\[\frac{1}{n} = \frac{4\pi}{3}a^3 \]

温度の記事で説明しますが、各粒子は基本的に、ランダムな方向に飛び交っています。 熱運動 脚注 [熱運動]：気体 (プラズマ) を構成する粒子たちの平均速度をその気体の流速と言います。流速と共に移動する観測者から見ても、各粒子たちはそれぞれ勝手な方向に運動しています。これを熱運動と言います。その速度分布の幅が温度です。具体的には、例えば電子の熱運動の速さの平均を \(\overline{v}_\text{e}\) としたとき、電子 1 個の持つ平均的な運動エネルギー \(m_\text{e}\overline{v}_\text{e}^2/2\) が \(k_BT_\text{e}\) に相当します。\(T_\text{e}\) は電子の温度です。ボルツマン定数 \(k_B = 1.38\times 10^{-23} \ \text{J K}^{-1}\) は温度とエネルギーの単位換算のための物理定数です。 と呼ばれるものです。1 つの粒子が持つ熱運動のエネルギーは平均的に \(k_BT\) と表されます。\(k_B=1.38\times 10^{-23} \ \text{J K}^{-1}\) はボルツマン定数、\(T\) は温度です。

以上の関係を用いることで、\(\Gamma\) は次のように表されます。

\[\Gamma = \frac{\phi_C}{k_BT} = \frac{e^2}{(4\pi)^{2/3}3^{1/3}\epsilon_0k_B}\frac{Q^2n^{1/3}}{T}\]

補足の先頭へ

各系の比較

上の節で紹介した各系のプラズマの大まかな密度と温度を 図 24 に示しました。横軸に数密度の対数スケール、縦軸に温度の対数スケールを取った平面上に表されています。

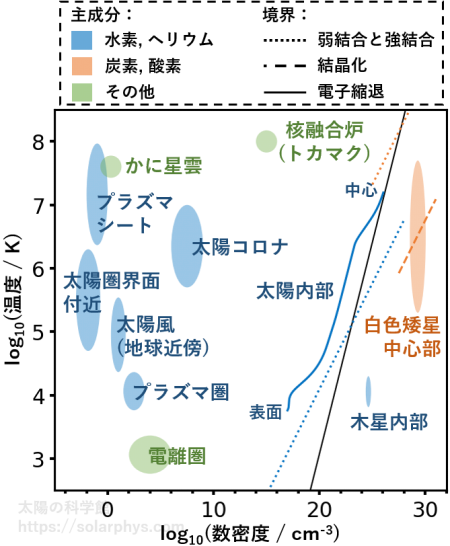
図 24   各系のプラズマの性質：横軸は数密度、縦軸は温度であり、どちらも対数スケールが用いられている。太陽内部については表面から中心までの変遷を曲線で表した。各プロットの色はプラズマの主成分の違いを表す。青色の境界は水素プラズマを想定したときのものであり、オレンジ色の境界は炭素プラズマを想定したときのもの。参考文献は次の通り。太陽内部：Christensen-Dalsgaard et al. (1996)、太陽コロナ：Cranmer (2009)、磁気圏と太陽風：Borovsky & Valdivia (2018)、太陽圏界面：Pogorelov et al. (2017)、木星内部：Helled et al. (2020) (温度)、Ni (2018) (密度)、かに星雲：Porth et al. (2014a)、白色矮星：Fontaine et al. (2013)、核融合炉：Goedbloed et al. (2019)。

図の青色の点線は水素イオン (陽子) と電子から成るプラズマを想定した場合の \(\Gamma = 1\) を表します。太陽内部は境界に近いですが、弱結合と言える領域です。木星内部は強結合です。

オレンジ色の点線は炭素イオン (価数 +6) と電子から成るプラズマを想定した場合の \(\Gamma = 1\) 、破線は \(\Gamma = 170\) を表します。高温の白色矮星は強結合プラズマですが、破線より低温の白色矮星は固体に相変化していると考えられています ( 例えば Kippenhahn et al., 2012; Fontaine et al., 2013 )。

電子の縮退

図 24 に書かれた黒い実線は、電子が縮退しているか否かの境界線です。線の右側にある系が縮退しています。ここでは詳しく述べませんが、縮退とは量子力学的な理由によって起きる現象です。縮退を考慮しなくても良い条件は次のように表されます。

\[ \frac{T^{3/2}}{n_\text{e}} \gg 10^{-22} \ \text{K}^{3/2}\text{m}^3 \]

太陽中心はこの境界に近くなっています。一般に、天体の内部のような高密度の系を考える際は、縮退の効果を考慮しなければならない場合がありますが、太陽外層や地球磁気圏のような十分に薄い系では気にする必要がありません。

相対性理論の必要性

かに星雲のシミュレーションでは特殊相対性理論が考慮されていると述べました。相対性理論とは、系のエネルギーが高い場合に必要になってくる理論です。次の全ての条件が満たされる場合、相対性理論を考慮する必要はありません。

  1. プラズマを構成する各粒子の速度が光速に対して無視できる。
  2. 重力が十分に弱く、静的である。重力が十分に弱いとは、重力ポテンシャル (単位質量あたりの重力による位置エネルギー) を \(\phi_g\)、光速を \(c=3.00\times 10^8 \ \text{m/s}\) としたときに、次の条件が満たされることである。

    \[\frac{|\phi_g|}{c^2}\ll 1\]

  3. 磁場が十分に弱い。具体的には次の条件を満たす。

    \begin{align} \frac{\text{磁場のエネルギー}}{\text{静止エネルギー}} &\equiv \frac{B^2/(2\mu_0)}{\rho c^2} \ll 1 \\ \text{ただし}, \quad B &: \text{磁場強度 [T]} \\ \rho &: \text{質量密度 [kg/m}^3\text{]} \\ \mu_0 &= 1.26\times 10^{-6} \ \text{T}^2\text{J}^{-1}\text{m}^3 \\ &: \text{真空の透磁率}\end{align}

太陽や地球磁気圏の場合について考えます。まず、条件 1 について、太陽フレアや CME に伴って発生する高エネルギー粒子 (SEP) は光速の 90 % に達することもあります ( 例えば Reames, 2021 )。また、地球磁気圏の放射線帯 (バンアレン帯) と呼ばれる領域には光速の 70 % 程の電子が存在します ( 例えば Borovsky & Valdivia, 2021 )。よって、これらの粒子が起こす現象を調べるためには、特殊相対性理論が必要になります。

それ以外の現象では、粒子の速度は光速に対して無視できます。例えば CME ではプラズマの流速が 3000 km/s に達することがありますが ( Manchester et al., 2017 )、光速に比べると 1 % 程度です。例えば温度が 1000 万 K の場合、電子の 熱運動 脚注 [熱運動]：気体 (プラズマ) を構成する粒子たちの平均速度をその気体の流速と言います。流速と共に移動する観測者から見ても、各粒子たちはそれぞれ勝手な方向に運動しています。これを熱運動と言います。その速度分布の幅が温度です。具体的には、例えば電子の熱運動の速さの平均を \(\overline{v}_\text{e}\) としたとき、電子 1 個の持つ平均的な運動エネルギー \(m_\text{e}\overline{v}_\text{e}^2/2\) が \(k_BT_\text{e}\) に相当します。\(T_\text{e}\) は電子の温度です。ボルツマン定数 \(k_B = 1.38\times 10^{-23} \ \text{J K}^{-1}\) は温度とエネルギーの単位換算のための物理定数です。 は光速の 4 % 程になりますが、まだ相対論的効果を考えなくて良い領域です。

条件 2 について、例えば太陽表面の重力ポテンシャルをゼロとし、Christensen-Dalsgaard et al. (1996) の質量密度分布を用いて計算すると、太陽中心は \(\phi_g = -7.7\times 10^{11} \ \text{J/kg}\) になります。これは \(|\phi_g|/c^2 \approx 10^{-7}\) であり、条件を満たします。

条件 3 について、例えば太陽表面の黒点には \(0.3 \ \text{T}\) の磁場が存在し、太陽表面の質量密度は \(10^{-4} \ \text{kg/m}^3\) 程度なので、条件式の値は \(10^{-9}\) 程度になります。従って、条件を満たします。

太陽-地球系の場合

このサイトが対象としている系 (太陽外層や太陽風、地球磁気圏、電離圏) は、弱結合でかつ縮退の効果が無視できるため、量子力学的な効果を考える必要がありません。また、上述した例外を除けば、多くの現象は相対性理論を考慮する必要もありません。よって、これらの系では、各々の粒子が高校で習う力学 (ニュートンの法則) に従って運動しているという描像が良い精度で機能します。

参考文献

記事全体として参考にした書籍

  • Goedbloed, H., Keppens, R. and Poedts, S. (2019). Magnetohydrodynamics of Laboratory and Astrophysical Plasmas ( Cambridge: Cambridge University Press ). 第 1 章から第 3 章.
  • Gurnett, D. A. and Bhattacharjee, A. (2005). Introduction to Plasma Physics: With Space and Laboratory Applications ( Cambridge: Cambridge University Press ). 第 1 章と第 2 章.

引用した文献

ご支援をお願いします。

運営にOFUSEする
記事一覧へ 次のカテゴリへ