ニュートリノ問題

太陽のエネルギー源

太陽は我々の頭上で輝き続けています。輝くことは光としてエネルギーを失うことです。太陽が 1 秒間に失うエネルギー (太陽光度、solar luminosity) は、地球で受け取る光エネルギーの測定から簡単に見積もることができ、\(L_\odot = 3.85 \times 10^{26} \ \text{W}\) であることが分かっています。国際エネルギー機関 (IEA) の統計によると、世界の年間電力消費量 (2017 年) は \(20000 \ \text{TWh}\) であり、この値から世界で平均的に 1 秒間に消費される電力量を計算すると、\(2\times 10^{12} \ \text{W}\) になります。この値と比べても、\(L_\odot\) はとてつもなく大きいことが想像できます。

生まれたばかりの太陽の光度は現在の 70 % 程であったと考えられていますが、それでも、それだけの光度で 45 億年間光り続けるには、強力なエネルギー源が必要です。それは中心部での核融合反応であると、現在では自信を持って言うことができます。

図 1 は太陽内部の温度と質量密度を表しています。どのようにしてこの図の値が得られるのかについては、記事「基本構造：何からできているのか？」で説明しています。

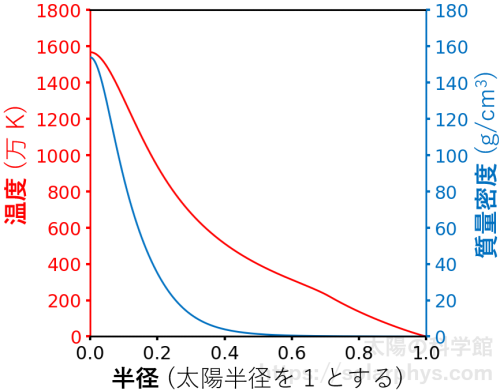
図を見ると、太陽内部は中心に行くほど温度も密度も高いことが分かります。表面温度 6000 \(\text{K}\) ( ケルビン 脚注 [ケルビン]：温度の単位には基本的にケルビン (K) を用います。日常で使われる摂氏と目盛の幅は同じであり，摂氏 0 度は 273.15 K です。つまり，例えば 300 K は摂氏 26.85 度のことです。 ) からどんどん上がり、中心部は 1500 万 \(\text{K}\) 程になります。

エネルギーは温度の高い方から低い方へと流れます。つまり、表面から宇宙空間に光として逃げて行くエネルギーを補うために、中心部から表面に向かうエネルギーの流れが存在します。そして、その源泉は中心部での核融合反応です。

核融合反応とは、次のような反応です。実際には下の節で説明するように、複数の段階を踏んだ反応が起きていますが、反応全体前後での収支としては 図 2 のように書けます。

4 個の水素イオン (陽子) から、1 個のヘリウムイオン (陽子 2 個と 中性子 2 個が結合した粒子) が作られます。反応の前後で電荷量は保存しなければならないため、電子 2 個も使われることになります。また、核反応の前後ではレプトン数という属性も保存されることが知られており、図の反応では 2 個のニュートリノが生成されます。極めて波長の短い光である ガンマ線 脚注 [ガンマ線]：電磁波 (光) のうち、波長が大体 \(10^{-12} - 10^{-11}\) m より小さい領域のものをガンマ線と言います。光子のエネルギーに換算すると、大体 100 keV - 1 MeV より大きな領域です。主に高エネルギー粒子の加減速や核反応によって発せられます。 も発せられます。

ニュートリノとは、電子の親戚のような粒子です。電子は \(9.11 \times 10^{-31} \ \text{kg}\) という質量を持ちますが、ニュートリノは質量がほぼゼロであることが知られています。これと関連して、ニュートリノは常にほとんど光速 (\(3 \times 10^{8} \ \text{m/s}\)) で飛んでいます。また、ニュートリノは電子と違って電荷を持たないため、 クーロン力 脚注 [クーロン力]：同じ符号の電荷を持った粒子の間には、互いに離れようとする力が働き、逆符号の電荷を持った粒子間には近づこうとする力が働きます。これをクーロン力と言います。クーロン力は粒子間の距離の 2 乗に反比例します。 のような電磁気的な力を感じることができません。このため、滅多に他の粒子と衝突することが無く、物質をすり抜けます。質量がほぼゼロなので重力もほとんど感じず、直進し続けます。

従って、太陽中心部での核融合反応によって生成されたニュートリノは、太陽をすり抜けて宇宙空間に逃げて行きます。そして、その一部は約 8 分かけて地球に到達し、我々の体も 1 秒間に 数百兆個というスケールでたくさん貫いているはずですが、我々がそれを認識することはできません。

上述した反応によってヘリウムが 1 個生成されると、\(4\times 10^{-12} \ \text{J}\) のエネルギーが解放されます。このエネルギーは生成されたニュートリノとガンマ線で分け合うことになります。ガンマ線はすぐに周りの粒子に吸収されて、熱エネルギーに変換されます。一方で、ニュートリノは先ほど述べたように、周りの物質にエネルギーを与えることなく宇宙空間に逃げて行きます。従って、解放されたエネルギーのうち、ニュートリノへの配分を差っ引いた分だけ、太陽の中心部は常に加熱されています。

図 3 に太陽内部での 2 種類の量の様子を示しました。赤で示したのは質量存在比と呼ばれ、水素やヘリウムが含まれる割合を表します。太陽はほとんど水素とヘリウムでできているので、両者の質量存在比を足すと 0.98 程度になります。青で示したのは核融合反応によるエネルギー生成率です。

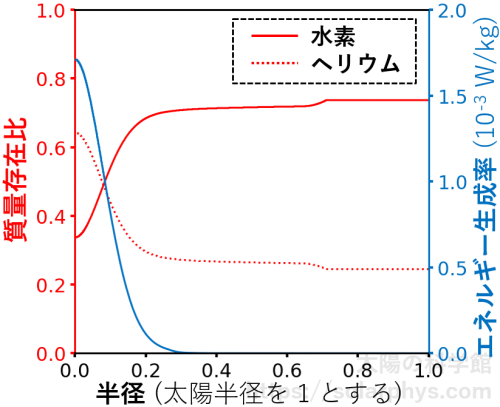
\(R_\odot\) を太陽半径とすると、核融合反応は主に半径 \(0.2R_\odot\) 以内の中心部で起きていることが分かります。核融合反応では水素が使われるため、中心部の水素は減っており、生成されるヘリウムの割合が増えています。

太陽は今まで 45 億年の間、水素を消費して光り続けてきました。この先更に 40 億年ほど経つと、中心部の水素は枯渇して核融合を起こせなくなると考えられています。すると、太陽は現在と同じようなバランスを保てなくなり、光度が \(2000L_\odot\) にもなる赤色巨星への進化が始まります。その過程で地球は太陽に飲み込まれてしまうだろうという試算もあります。太陽の進化について詳しくは、例えば Christensen-Dalsgaard et al. (2020) を参考にしてください。

ニュートリノの数が少ない？

核融合反応が太陽のエネルギー源になり得るのではないかというアイデアが提案されたのは 1920 年代です。しかし、当時の原子核物理学の知見では、太陽中心の温度では核融合は起き得ないとみなされていました。太陽内部では、水素は 電離 脚注 [電離]：粒子が電子を手放して電荷を持つようになることを電離と言います。電荷を持った粒子を含む気体をプラズマと言います。一部の粒子のみが電離している状態を部分電離または弱電離と言います。 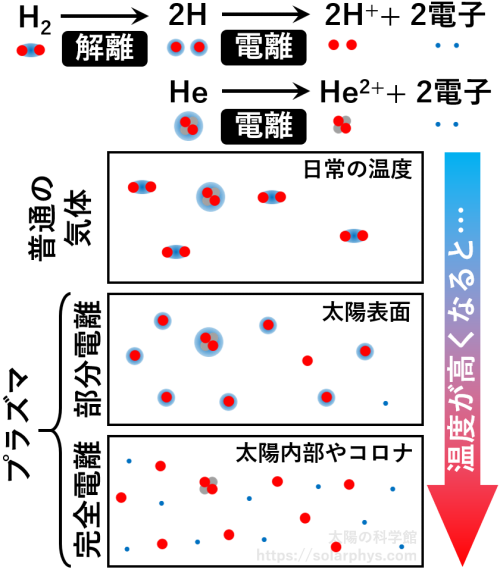した状態で存在するため、核融合が起きるには、正電荷を持った水素イオン同士が、クーロン力による反発の壁を越えて衝突する必要があります。太陽中心の 1500 万 \(\text{K}\) 程度の温度では、これは無理であろうと考えられていたのです。この謎は核融合の研究を発展させ、後に、量子力学のトンネル効果を考慮すれば、太陽中心の環境でも核融合を起こせることが分かりました。こうして、核融合がエネルギー源として強く信じられるようになりました。

図 1 や 図 3 は標準太陽モデルと呼ばれます。詳しくは 基本構造の記事 で説明していますが、中心部での核融合反応による発熱機構も考慮したうえで、理論的に求まった値です。このような標準太陽モデルで得られた密度や圧力の値は、観測に基づく推定とも良い精度で一致しています。このことからも核融合の存在が予言されます。

太陽中心で核融合が起きているのかどうかを確かめる直接的な方法は、核融合によって生成されるニュートリノを観測することです。太陽の方角から地球に飛んで来るニュートリノの数が、理論から予言される値と一致すれば、核融合の存在が証明されることになります。

初めてニュートリノの観測が行われたのは 1960 年代で、米国のホームステイク鉱山に設置された検出器でした。これは、ニュートリノが稀に起こす

\[\text{ニュートリノ}+\text{Cl}\longrightarrow\text{電子}+\text{Ar}\]

という反応を利用した試みでした。615 トンのテトラクロロエチレン (\(\text{C}_2\text{Cl}_4\)) の液体をタンクに溜め、一定時間が経ったら回収してタンク内に生成された \(\text{Ar}\) を数え上げます。前述したように、ニュートリノは他の粒子とごく稀にしか反応を起こさないため、統計的な解析を行うのに十分な数を観測するためには、大量の反応液と長い観測時間が必要になります。

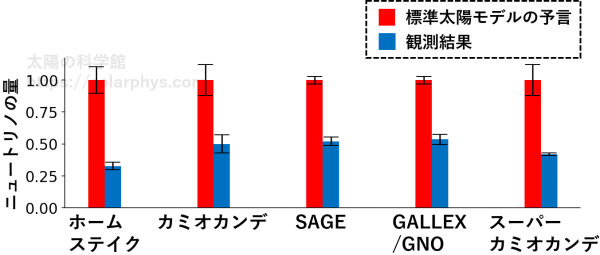
当時の標準太陽モデルの核融合反応数を基に、ホームステイクの検出器で得られるであろうニュートリノ数が推定されましたが、実際に得られた数は、その予言値の 3 分の 1 程度しかありませんでした。

2 番目に開発されたニュートリノ検出器は、 1980 年代、日本のカミオカンデです。これは、3000 トンの水を水槽に溜めた装置です。地球に降り注ぐニュートリノは稀に、水槽内の電子と衝突します。このときに発生する僅かな光を水槽の壁にたくさん取り付けられたセンサーで検出します。

カミオカンデはニュートリノの飛来方向まで測定することができ、観測されるニュートリノが本当に太陽の方角からやってきていることを明らかにしました。しかし、観測される数は、やはり標準太陽モデルの予言の半分程度でした。

カミオカンデに続いて、ロシアに SAGE、イタリアに GALLEX、更にカミオカンデの後継機としてスーパーカミオカンデと、新たなニュートリノ検出器が開発され、地球に飛来するニュートリノ数が複数の検出方法で観測されましたが、どれも標準太陽モデルの予言より少ない結果となりました。図 4 に各検出器の結果を示します。

標準太陽モデルが間違っているのか？

なぜ理論の予想よりも少ない数が観測されてしまうのか？様々な方向性の解決案が考え出されました。

まず考えられるのは、標準太陽モデルが間違っている可能性です。モデルの太陽中心温度を低くすれば、観測されるニュートリノ数に合わせることも可能なため、どうすれば中心温度を下げられるかが議論されました。例えば、次のような案が出されました。

• 図 3 では中心部の水素の質量存在比が少なくなっているが、中心部とその周りをかき混ぜる何らかの「スプーン」のような機構が存在すれば、中心部の水素は多くなるはずである。すると、核融合の様式が変化して、話が変わるかもしれない。
• 太陽は水素が 70 % 程度、ヘリウムが 28 % 程度で構成されているが、表面の観測からはより重い元素も少量 (合わせて 2 % 程度) 含まれていることが分かっている。標準太陽モデルでは、この重い元素の割合は太陽内部でも同じであろうと仮定しているが、実は惑星から重い元素が降り積もることで、表面だけが例外的に重い元素を多く含んでいるのだとしたら、話が変わるかもしれない。
• いわゆる「ダークマター」 (未解明の物質) が太陽内にも存在していると考えれば話が変わるかもしれない。

詳しくは記事「太陽内部を探る日震学」で説明していますが、太陽表面で観測される気体の振動を解析することで、太陽内部の密度や圧力などの情報を得ることができます。この手法を 日震学 脚注 [日震学]：太陽表面で観測される気体の振動や波を解析することで、太陽内部の圧力や密度、流れの様子などを知ることができます。この手法を日震学と言います。日震学はこれまで、太陽内部の理論モデル (標準太陽モデル) の観測的裏付けを与えた他、太陽内部の自転 (差動回転) の様子も明らかにしました。 と言います。標準太陽モデルの密度や圧力は日震学による推定と良い精度で合致しています。

標準太陽モデルに上で挙げたような改正案を盛り込むと、日震学の結果や他の天体の観測結果などとの辻褄が合わない部分が出てきます。このことから、標準太陽モデルは間違っていないのではないかと考えられました。

それならば、ニュートリノ物理学が間違っているのかもしれない、ということで有力な候補に挙がったのが「ニュートリノ振動 (neutrino oscillation)」と呼ばれる現象です。

ニュートリノ振動の発見

ニュートリノ振動を考えれば解決？

この宇宙を構成する物質は全て、何種類かの粒子の組み合わせでできている、というのが現代の物理学の基本的な考え方です。そして、その基本の構成要素を「素粒子 (elementary particle)」と言います。例えば電子やニュートリノは素粒子です。陽子や中性子は 2 種類の「クォーク」という素粒子の組み合わせでできています ( 図 5 )。

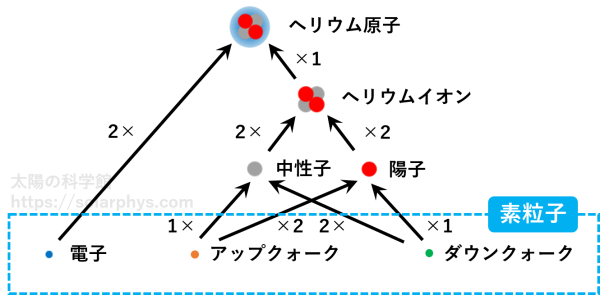
物理学の目標のひとつは、この素粒子を全て見つけ出し、それらの個性や他の素粒子との関係性を調べ上げ、その全てを説明することができる数学的枠組みを完成させることです。

ニュートリノには「電子型」「ミュー型」「タウ型」の 3 種類が存在します。太陽中心の核融合 ( 図 2 ) で、消費される電子の代わりに生成されるニュートリノは、このうちの電子型です。

太陽ニュートリノ問題の発見以前から構築されていた「標準模型」という素粒子理論の枠組みでは、3 種類のニュートリノはそれぞれ独立に存在し、違う型に変化することはないとされていました。そう考えると数学的に綺麗な枠組みを構築することができたのです。

このため、太陽中心で生成された電子型ニュートリノは、数を変えることなく地球に飛来すると考え、各検出器は電子型ニュートリノの数を数えていました。

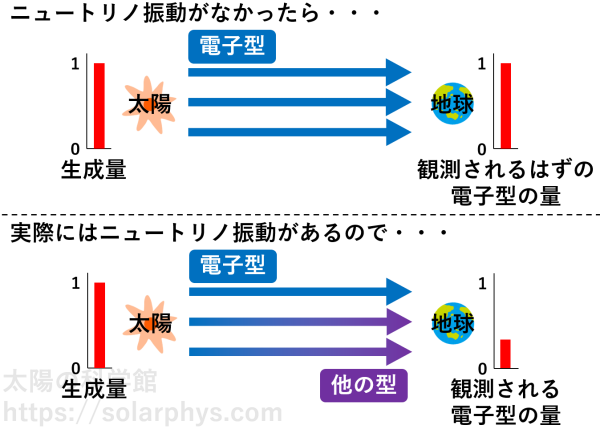
観測される電子型ニュートリノの数が足りないという問題は、太陽中心で生成された電子型ニュートリノの一部が、地球まで飛んでくる過程で別の型のニュートリノに変化していると考えれば説明することができます ( 図 6 )。この現象をニュートリノ振動と言います。各検出器は他の型に変化しなかった一部のニュートリノのみを数えているわけです。

大気ニュートリノの観測

ニュートリノ振動の存在が初めて統計的に示されたのは 1998 年でした。これは、太陽の核融合で発生するニュートリノではなく、地球の高層大気で生成されるニュートリノをスーパーカミオカンデで観測した結果から得られたものでした。

地球には、宇宙から高エネルギーの粒子が常に降り注いでいます。「宇宙線」と呼ばれる現象です。それらの粒子はしばしば、地球大気を構成する物質と衝突します。それに伴って、ミュー型ニュートリノが生成されることがあります。このような仕組みで生成されたニュートリノは「大気ニュートリノ」と呼ばれることで、太陽など他の原因によって生成されたニュートリノと区別されます。

大気ニュートリノは、太陽ニュートリノよりも高いエネルギーを持ち、飛来方向も様々であるため、スーパーカミオカンデのような検出器では両者を区別することができます。また、スーパーカミオカンデは電子型ニュートリノに加え、ミュー型ニュートリノも捉えることができます。

スーパーカミオカンデは、ミュー型の観測を行うことで、次のことを発見しました。検出器に上から飛来した大気ニュートリノは、理論から予想される数と一致した一方で、下から飛来した数は、理論の予想を下回りました。この結果は次のことを意味します。

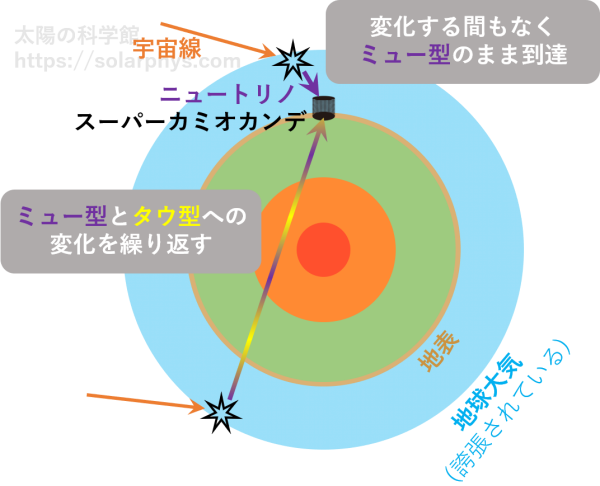
図 7 を見てください。スーパーカミオカンデに上から飛来する大気ニュートリノは、上空で生成されてから短い距離を飛行して検出器に到達したものです。一方で、下から飛来するものは、地球の反対側の大気で生成され、地球内部を長い距離飛んできたものです。生成されたミュー型の一部が他の型に変化するには一定の時間が必要であり、薄い地球大気を飛んだ程度ではニュートリノ振動はまだ起こりません。

従って、スーパーカミオカンデに上から飛来したものは、他の型に変化する間もなく、生成されたままのミュー型として、全てが観測されます。一方で、下から飛来するものは、ニュートリノ振動を既に起こしているため、他の型に変化していない一部のミュー型しか観測されません。

こうして、ミュー型ニュートリノの一部がおそらくタウ型に変化していることが示されました。更に詳しくは、例えば スーパーカミオカンデのサイト内の記事 や 梶田 (2015) を読んでください。

太陽ニュートリノ問題の解決

太陽ニュートリノ問題への決定打は 2002 年、カナダに建設された検出器 SNO によってなされました。SNO は太陽から来る電子型ニュートリノに加え、ミュー型とタウ型の数の測定にも成功しました。そして、3 つの型で合計したニュートリノ数は標準太陽モデルの予言に一致しました ( 図 8 )。

このような経緯を辿って、現在ではニュートリノ振動の存在は強く信じられるようになっています。太陽ニュートリノや大気ニュートリノ、あるいは原子力発電炉や加速器で人工的に生成されたニュートリノを観測することで、ニュートリノ振動の性質を詳細に調べる研究が各国の検出器で行われています。また、理論の面でも、従来の標準模型を拡張して、いかにニュートリノ振動を枠組みの中に取り入れるかの研究が行われています。

また、観測されるニュートリノ数の問題が解決されたことにより、ニュートリノを用いて太陽内部を「透視」できる時代が訪れました。今まで、太陽内部を調べる方法は 日震学 脚注 [日震学]：太陽表面で観測される気体の振動や波を解析することで、太陽内部の圧力や密度、流れの様子などを知ることができます。この手法を日震学と言います。日震学はこれまで、太陽内部の理論モデル (標準太陽モデル) の観測的裏付けを与えた他、太陽内部の自転 (差動回転) の様子も明らかにしました。 に限られていましたが、ニュートリノの観測精度が上がれば、太陽内部の状態についての新たな情報が得られることが期待されます。

素粒子で地球を透視する

太陽物理だけでなく、地球科学に関しても同様のことが言えます。地球内部には幾分か、ウランやトリウムのような放射性元素が存在していると考えられています。これらの元素は自然に崩壊を起こし、より軽い元素に変化していきます ( 図 9 )。このときに発生する熱は、地球を温める大きな要因のひとつと考えられており、地球内部の状態を議論する際に考慮せねばならない要素です。

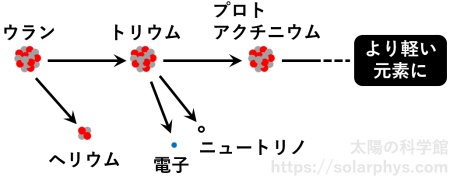
しかし、地球内部の放射性元素が具体的にどのように分布しているのかを直接的に観測することはまだできていません。この崩壊に伴って生成されるニュートリノを高い精度で観測することができれば、将来的にはそれが可能になるかもしれません ( 田中, 2016 )。

ニュートリノとは別の素粒子に「ミュー粒子」と呼ばれるものがあります。この粒子も、宇宙線が大気に衝突するときに生成されるため、我々の周りを常に飛び交っています。この粒子を用いて火山の内部などを「透視」する技術は、ニュートリノよりも一足先に、実用化されつつあります。

ミュー粒子はニュートリノとは違って電荷を持つため、物質を構成する粒子と頻繁に衝突します。岩石を最大で数 km 程度すり抜けて直進することができますが、中には途中で岩石を構成する粒子と衝突してエネルギーを失い、透過できないものもあります。この透過率は岩石の厚みや密度で決まります。

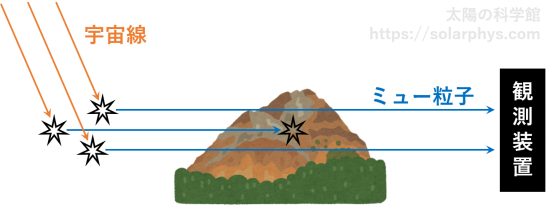
よって、例えば火山をすり抜けてくるミュー粒子の数を観測することで、火山の内部の密度 (マグマの様子) を知ることができます ( 図 10 )。この技術は「ミュオグラフィ」と呼ばれます。ニュートリノの場合はスーパーカミオカンデのような巨大な検出器が必要ですが、ミュー粒子の検出にはそこまでのコストを必要としないため、研究が進んでいます。詳しくは例えば 東京大学のサイトに掲載された記事 を読んでください。

核融合反応とは何か

太陽の中心部で起きている核融合は、反応前後の収支としては 図 11 のように書けることを述べました。この反応についてもう少し詳しく説明します。

解放されるエネルギーの源

エネルギーは様々な形態を取ります。例えば、ソーラーパネルは光のエネルギーを電気エネルギーに変換する装置です。あるいは、コンロで火をつけると、燃料のガスが持っていた化学エネルギーの一部が熱エネルギーと光のエネルギーに変換されます。

物質の質量もエネルギー形態のうちのひとつです。核融合反応は、水素が持っている質量の一部を光 (ガンマ線) のエネルギーやニュートリノのエネルギーに変換する反応です。既に述べたように、ガンマ線のエネルギーはその後すぐに、太陽中心部の熱エネルギーとなります。

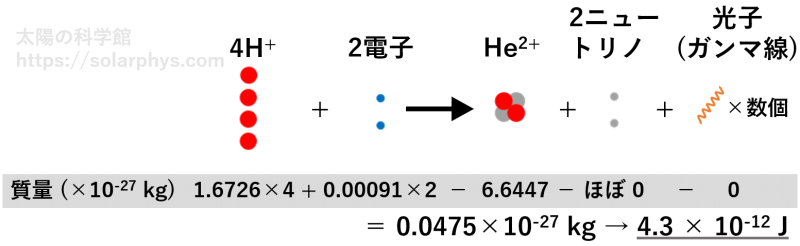
図 12 のようにして、反応前の粒子の総質量から反応後の総質量を引くと、\(4.75 \times 10^{-29} \ \text{kg}\) となります。この質量の消失分だけのエネルギーがニュートリノとガンマ線に配分されるわけです。質量 \(m \ [\text{kg}]\) とエネルギー \(E \ [\text{J}]\) の単位換算は次の式で行えます。

\[E=mc^2\]

ただし、\(c=3.00\times 10^8 \ \text{m/s}\) は光速です。この式を用いると、ヘリウムイオンが 1 個生成されるごとに \(4.3 \times 10^{-12} \ \text{J}\) のエネルギーが解放されると見積もることができます。

具体的な反応

反応というものは、粒子と粒子が衝突する ( = 十分に近づく) ことで起きます。それぞれが勝手に飛び交っている中で、3 つの粒子が同時に衝突する確率は、 2 つの粒子が衝突する確率に比べて低いです。 4 つ以上の粒子が 1 箇所で同時に衝突するなんてことは奇跡に近いです。

図 11 では、核融合に必要な材料は陽子 (水素イオン) 4 個と電子 2 個と書きましたが、実際にこの計 6 個の粒子が同時に衝突し、ヘリウムを生成するようなことはまず起こりません。実際の核融合反応は 2 個 (たまに 3 個) の粒子の衝突によって起こる反応の組み合わせによって進行します。幾重もの反応の結果、最終的にヘリウムが生成されるわけです。

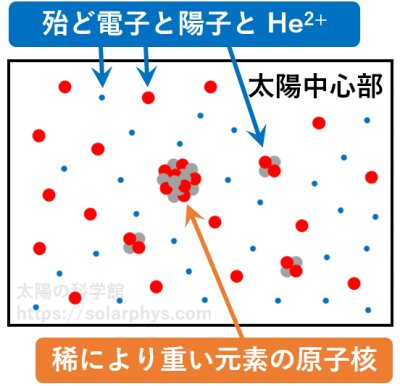
太陽中心部の状態の模式図を 図 13 に示しました。存在する物質粒子のほとんどは電子 (水素イオン) と陽子とヘリウム原子核 (ヘリウムイオン) であり、それぞれ勝手に飛び交っています。稀に、より原子番号の大きい元素の粒子が飛んでいます (質量にして 2 % 程度)。

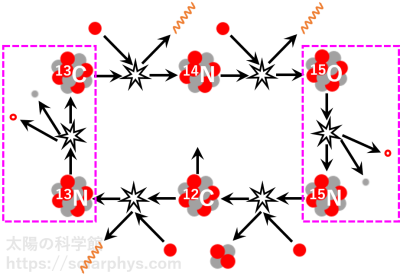
たくさん飛んでいる粒子種同士の衝突はたくさん起きます。衝突が起きた時に解放されるエネルギーは反応によってまちまちです。衝突確率や解放されるエネルギーの具体的な値は、実験と理論から計算することができます。それを踏まえて、太陽中心部の加熱に大きく寄与している核反応の組み合わせとして、「pp チェイン」「CNO サイクル」の 2 つが存在すると考えられています。前者は中心部の加熱に使われるエネルギー全体の 99 %、後者は残りの 1 % を担っています。

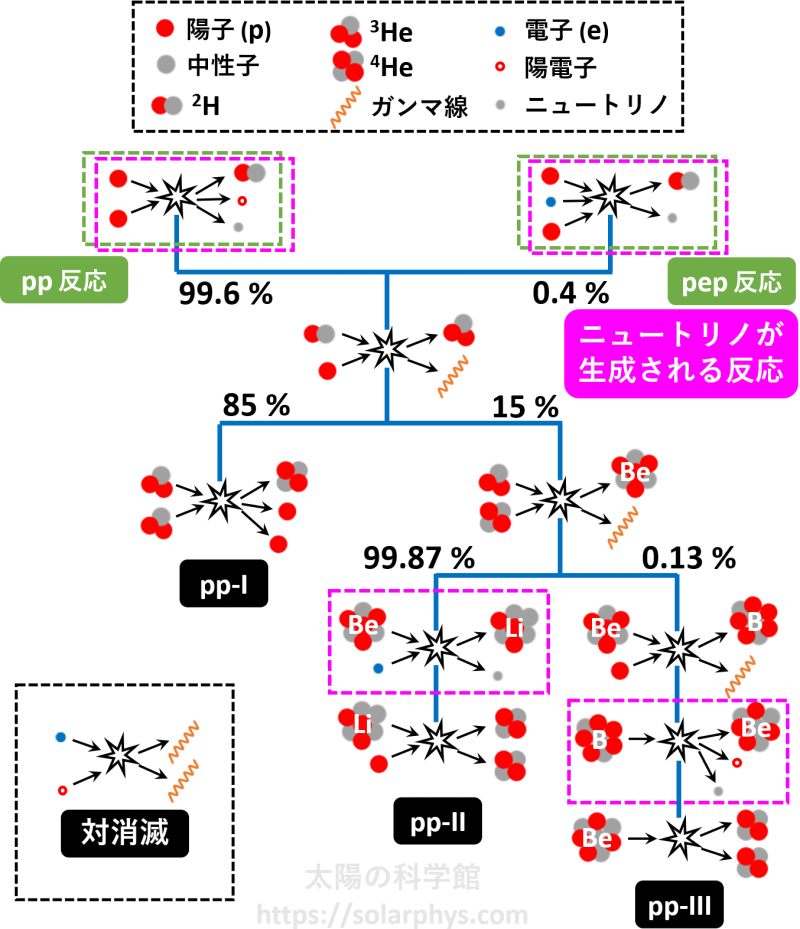
図 14 に pp チェインの全体像を示しました。反応の樹形図は最終的に 3 つに分岐しています。各系統は pp-I、pp-II、pp-III という名前が付いており、それぞれ pp チェイン全体が生むエネルギーの 77 %、23 %、 0.02 % を占めています。

図 15 は CNO サイクルの全体像です。こちらの反応系統では、重い元素を触媒として、ヘリウムが生成されます。

ニュートリノの観測

図 14 と 図 15 でピンク色の枠で囲った反応は、ニュートリノを生成する反応です。pp チェインの図に示した反応の中では pp 反応、 pep 反応、Be の崩壊、B の崩壊の 4 つが該当します。

これらの反応ごとに異なるエネルギーを持ったニュートリノが放出されます。ニュートリノ検出器は、引っかかったニュートリノが持つエネルギーも測定することができるため、そのニュートリノがどの反応に由来するものなのかを仕分けることができます。

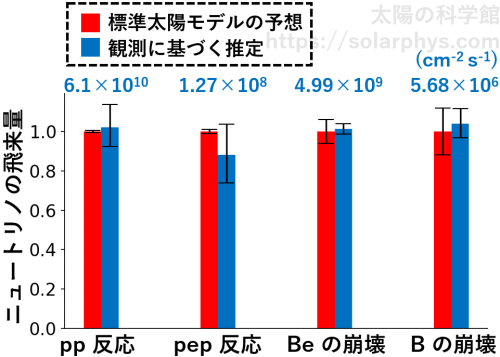
例えばイタリアに建設された検出器 Borexino の場合、300 トンの反応液を用いてニュートリノを待ち構えます。すると、1 日あたり & 100 トンの反応液あたりに 100 個程度の pp 反応由来のニュートリノを捉えることができます ( Agostini et al., 2018 )。

ニュートリノ振動の性質は今や分かっているので、標準太陽モデルと併せれば、地球に届くニュートリノのうちの何割がどの型であるかは計算することができます。また、各型のニュートリノが Borexino に飛んできたときに検出できる確率も計算できるため、Borexino が検出したニュートリノ数から、地球に飛来している全型の合計数を推定することができます。

そうして求まった Borexino の観測結果と、標準太陽モデルの予想との比較を各反応ごとに示したものが 図 16 です。両者は大体一致していることが分かります。このことは、pp チェインの核反応が実際に起きていることが観測に基づいて確かめられたことを意味します。

図に載せたように、地球に飛来しているニュートリノ数が観測されれば、太陽内部で生成されているニュートリノ数、すなわち起こっている核融合反応の数も推定できます。すると、太陽内部が現在どれくらい加熱されているのかも推定することができます。

Borexino が推定した結果は \(L = 3.89^{+0.35}_{-0.42}\times 10^{26} \ \text{W}\) であり、地球で観測される太陽光強度から計算される太陽光度 \(L_\odot =3.85 \times 10^{26} \ \text{W}\) と一致します。このことは、現在の太陽が失っているエネルギー量と獲得しているエネルギー量が一致していて、太陽全体のエネルギー収支のバランスが保たれていることを意味します。

ニュートリノ振動とは何か

ニュートリノは実験施設で観測できる限りの精度では光速で運動します。相対性理論によると、正確に光速で運動する粒子は質量が正確にゼロであることが言えます。太陽ニュートリノ問題以前の素粒子理論 (標準模型) によると、理論の枠組みを綺麗にするためにはニュートリノの質量は正確にゼロでなければなりませんでした。しかし、ニュートリノ振動の発見によって、その枠組みは修正を迫られました。

ニュートリノには質量が正確にゼロではないものが存在するのです。ニュートリノ振動の性質が調べられることによって、3 つの型の質量の間の関係性は分かってきましたが、それらの質量の絶対値を測定することはまだできていません。少なくとも \(2\times 10^{-36} \ \text{kg}\) 以下であることは分かっています ( Aker et al., 2019 )。参考として、電子の質量は \(9 \times 10^{-31} \ \text{kg}\) です。

ニュートリノ振動が起きているという事実は、次の 2 つのことを意味します ( 例えば Suekane, 2015 )。

• ニュートリノには質量が正確にゼロではないものがある。
• 量子力学的な難しい言い方をすると、ニュートリノの型 (電子，ミュー，タウ；専門用語ではフレーバーと呼ばれます) の固有状態と質量の固有状態は異なる。

何を言っているのか分からない方のために、なるべく優しい説明を試みます。まず、タウ型のことは忘れて、ニュートリノは電子型とミュー型の 2 種類であるとします。すると、光の偏光との対応を考えることで、理解がしやすくなると思います。

偏光については記事「偏光とは何か？：光の持つ 2 つの状態」で説明しています。以降の説明を読む前に、偏光の記事の円偏光に関する節まで読んでいただければ、分かりやすくなると思います。

1/4 波長板の仕組み

偏光の記事 で 1/4 波長板という装置が出てきました。これは直線偏光を円偏光に変換する装置です。この装置の仕組みを説明します。

真空中の電磁波は光速 \(c = 3.00 \times 10^8 \ \text{m/s}\) で伝搬します。空気中でもそれに近い速さです。しかし、結晶の中を伝搬する際には、速度が遅くなります。結晶内での伝搬速度が \(c/n\) であった場合、\(n\) をその結晶の屈折率と言います。例えば水晶の屈折率は \(n = 1.5\) 程度です。

鉱物の中には複屈折という性質を持つものがあります。これは、電磁波の偏光状態によって伝搬速度が異なるという性質です。特定の軸の方向を向いた直線偏光は比較的速く伝搬し、それに垂直な軸方向の直線偏光はより遅く伝搬します。前者を速軸、後者を遅軸と呼ぶことにします。

1/4 波長板はこの性質を利用した装置です。1/4 波長板の速軸 (\(x\) 軸) と遅軸 (\(y\) 軸) に対して 45 度傾いた直線偏光を入射させた場合を考えます ( 図 17 )。入射光は \(x\) 偏光と \(y\) 偏光の和と解釈できます。両者は波長板内部では異なる速度で伝搬するため、出射される頃には位相のずれが生じます。

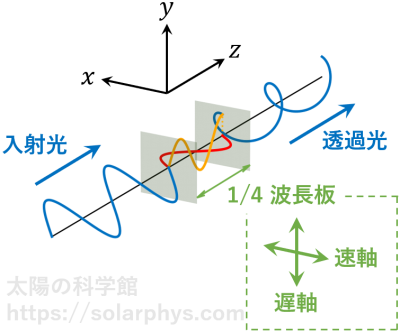
1/4 波長板はその位相のずれが 1/4 波長分になるように厚さを調整して作られた装置です。このため、透過光は 2 つの直交する直線偏光を 1/4 波長分だけずらして重ね合わせた波、すなわち円偏光になります。

ニュートリノ振動との対比

量子論によると、素粒子は波の性質を持ちます。これはニュートリノの型のような状態が、光の場合の偏光状態と類似した数学によって記述されることを言っています。

右円偏光と左円偏光の光がそれぞれ電子型とミュー型のニュートリノに対応すると考えてください。核融合で生成されるニュートリノは電子型です。右円偏光は 2 つの直交する直線偏光に分解して解釈することができました ( 図 18 )。この対比として、電子型ニュートリノは「1 型」と「2 型」の重ね合わせとして解釈できます。

仮に 1 型と 2 型の質量が両方とも正確にゼロだったならば、真空中の電磁波と同じ状況です。1 型も 2 型も同じ速さで位相が伝搬します。右円偏光がずっと右円偏光として伝搬するように、生成された電子型はずっと電子型として地球まで飛来するはずです。

しかし、1 型と 2 型の少なくとも一方の質量が正確にゼロではなく、両者に質量差が存在する場合は、1/4 波長板内部の電磁波と同様の状況になります。1 型と 2 型の位相が伝搬する速度に違いが現れるため、ニュートリノが移動するごとに両者の位相がずれていきます。

右円偏光を分解したときの 2 つの直線偏光の位相が相対的に 1/2 波長分ずれると、重ね合わせの結果は左円偏光に変化します。これとの対比で、1 型と 2 型の位相がずれていくと、初め電子型だったニュートリノはやがてミュー型に変化します。これがニュートリノ振動です。

複屈折を持つ結晶の内部で、初めに右円偏光にあった光が左円偏光との間の変化を繰り返す頻度は、速軸 (f) と遅軸 (s) の屈折率の差 \(\Delta n = n_\text{s}-n_\text{f}\) に依存します。対して、初めに電子型にあったニュートリノがミュー型との間で変化を繰り返す頻度は、 1 型と 2 型の質量の 2 乗差 \(\Delta m^2 = m_1^2-m_2^2\) に依存します。

例えば直線偏光に右円偏光を透過するフィルターをかざしたとき、透過光の強度は元の 1/2 になります。この要領で、純粋な電子型ではない状態のニュートリノの集団を観測すると、捉えられる電子型の数は元よりも少なくなります。これが太陽ニュートリノ問題の根本です。

参考文献

記事全体として参考にしたレビュー

• Christensen-Dalsgaard, J. (2021). Solar structure and evolution. Living Reviews in Solar Physics, 18, 2 .

引用した文献

• Agostini, M., Altenmüller, K., Appel, S. et al. (Borexino Collaboration). (2018). Comprehensive measurement of pp-chain solar neutrinos. Nature, 562, 505–510 .
• Aker, M., Altenmüller, K. and Arenz, M. et al. (KATRIN Collaboration). (2019). Improved upper limit on the neutrino mass from a direct kinematic method by KATRIN. Physical Review Letters, 123, 221802 .
• Christensen-Dalsgaard, J., Däppen, W., Ajukov, S. V., Anderson, E. R., Antia, H. M., Basu, S., Baturin, V. A., Berthomieu, G., Chaboyer, B., Chitre, S. M., Cox, A. N., Demarque, P., Donatowicz, J., Dziembowski, W. A., Gabriel, M., Gough, D. O., Guenther, D. B., Guzik, J. A., Harvey, J. W., Hill, F., Houdek, G., Iglesias, C. A., Kosovichev, A. G., Leibacher, J. W., Morel, P., Proffitt, C. R., Provost, J., Reiter, J., Rhodes Jr., E. J., Rogers, F. J., Roxburgh, I. W., Thompson, M. J. and Ulrich, R. K. (1996). The current state of solar modeling. Science, 272, 1286-1292 .
• Suekane, F. (2015). Neutrino Oscillations: A Practical Guide to Basics and Applications (Tokyo: Springer Japan ).
• 梶田 隆章. (2015). 大気ニュートリノとニュートリノ振動. Kavli IPMU News, 31, 30-35 .
• 田中 宏幸. (2016). ニュートリノを用いた地球内部のイメージング. 地学雑誌, 125, 647-659 .