電磁波の振動方向
光は「偏光」と呼ばれる性質を持ちます。記事「プラズマ診断:太陽を「見る」だけでここまで分かる」で説明していますが、太陽から来る光の偏光状態を知ることで、太陽表面の磁場の様子についての情報を得ることができます。偏光についての知識は天文学において不可欠です。
記事「光とは何か?」で説明していますが、光は電磁波と呼ばれる波として考えることができます。空間中の各点において、電場というものを考えることができます。ある点での電場が何らかの原因によって乱されると、その乱れが隣の点での電場を乱し、更に隣の点での電場が乱され ... という形で、電場の揺らぎが空間中を伝わります ( 図 1 )。その伝搬速度は基本的に光速 \(3 \times 10^{8} \ \text{m/s}\) です。これが電磁波の基本的な考え方です。
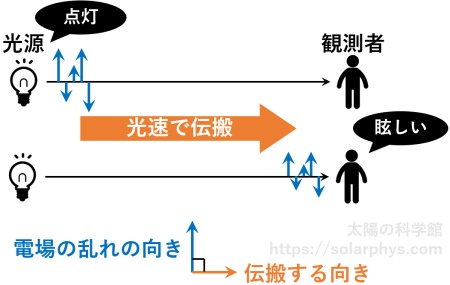
電磁波は横波なので、伝搬する方向と電場の乱れの方向は必ず垂直でなければなりません。図 1 は 2 次元的に簡略化されたイメージですが、3 次元的に考えるともう少し複雑です。
図 2 のように、\(z\) 軸正の向きに伝搬している光を考えます。なお、以後の説明でも一貫して \(z\) 方向が伝搬方向です。このとき、図の赤色で示した波のように、電場が \(y\) 方向に振動するような波は存在し得ます。また、青色で示したように、 \(x\) 方向に振動する波も許されます。あるいは、\(z\) 軸に垂直な方向ならば、それ以外の向きに振動するような波もあり得ます。

このように、同じ \(z\) 方向に伝搬する電磁波でも、電場の振動する方向は様々なパターンがあり得ます。この違いを偏光と言います。例えば、図 2 に赤で示したような波は、「\(y\) 方向に直線偏光している」と形容されます。
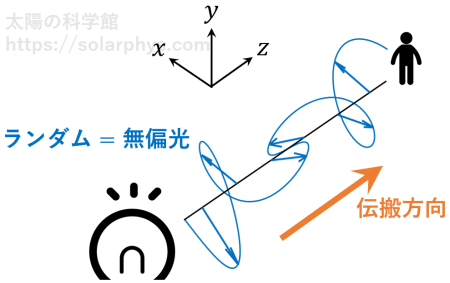
普通の電灯の光は、\(z\) 軸に垂直な向きという条件は満たしつつ、時と場所によってランダムな方向に電場が振動しています ( 図 3 )。このような光は「無偏光」の状態にあると呼ばれます。
偏光とはどんなものか
偏光とはどのようなものであるのかを視覚的に感じていただくために、 図 4 の 2 つのフィルターを用意しました。左は偏光板、右は C-PL フィルターと呼ばれます。 C-PL フィルターは本来カメラに取り付けて、反射などを抑えた写真を撮るために用いられるものです。

偏光板は、 図 4 に記した矢印の方向に直線偏光した光のみを透過する装置です。この矢印の向きを透過軸と呼ぶことにします。偏光板にも値段相応の精度があり、現実には透過軸方向の直線偏光もロス無く透過することはないのですが、以下では図の偏光板が理想的な装置であると仮定して説明します。つまり、強度 (明るさ) が 1 である透過軸方向の直線偏光を通した場合、すり抜けた光の強度は 1 であるとします。
無偏光とは、様々な偏光状態がランダムに混ざったような性質です。無偏光を偏光板に通すと、その中の透過軸方向の直線偏光成分のみが抽出されます ( 図 5 )。すり抜けた光の強度は (理想的な装置の場合) 元の 1/2 になります。透過軸の方向を変えると、その向きの直線偏光が抽出されるようになりますが、透過光の強度は変化しません。図 4 を見ると、確かに偏光板を通して見える背景は暗くなっています。
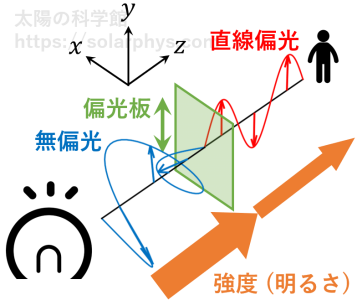
私が所有するパソコンの画面は、水平に直線偏光した光を発します。透過軸の向きを変えながら画面を偏光板越しに見た様子を 図 6 に示します。

図の (C) の場合は、画面が発する直線偏光の向きと透過軸が一致しているので、画面の光は (理想的には) 全て透過します。一方で、(A) の場合は、透過軸が偏光方向と直交するため、画面の光は全て遮断されます。透過軸を斜めにした (B) の場合は一部の光が透過しており、画面が暗く見えます。
図 6 で何が起きているのかをイメージしたものが 図 7 です。(A) の場合、画面の光は透過軸方向の直線偏光成分を持たないため、透過される光はゼロです。逆に (C) の場合は、画面の光は透過軸方向の直線偏光なので、全てがそのまま透過されています。
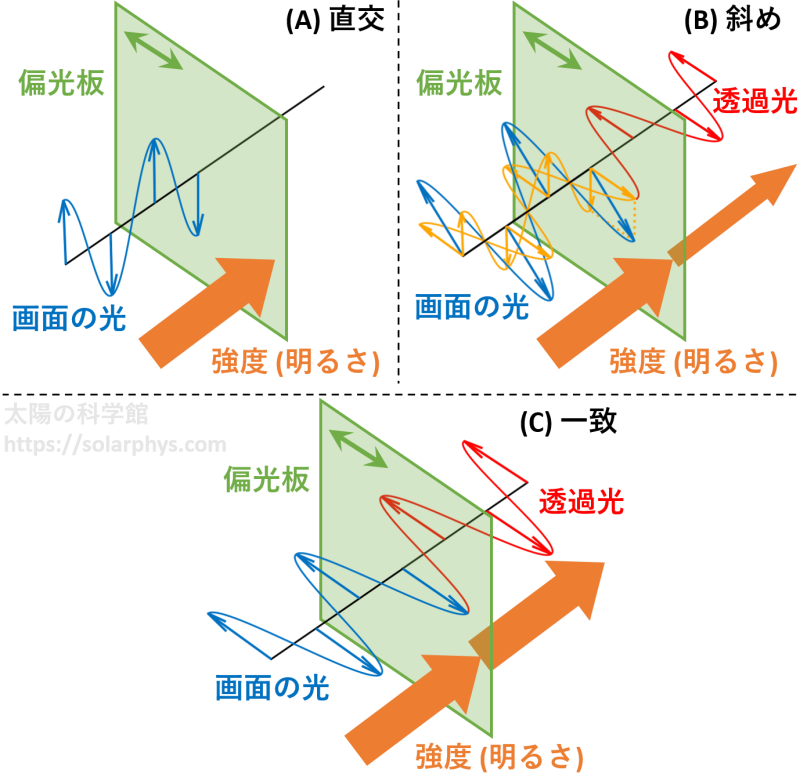
(B) の場合、画面の光 (図の青) は斜め方向の直線偏光をしていますが、これは図に黄色で示したように、2 つの直線偏光が足し合わされたものと解釈できます。このうちの透過軸に一致する方向の直線偏光成分のみが透過されます。透過された光の強度は元より小さくなります。
円偏光
直線偏光が 2 つの直線偏光の和と解釈できると述べました。図 8 (A) のように、強度が等しく、互いに直交する向きの 2 つの直線偏光 (黄色) を数学的 (ベクトル的) に足し合わせると、45 度傾いた直線偏光を作ることができます。
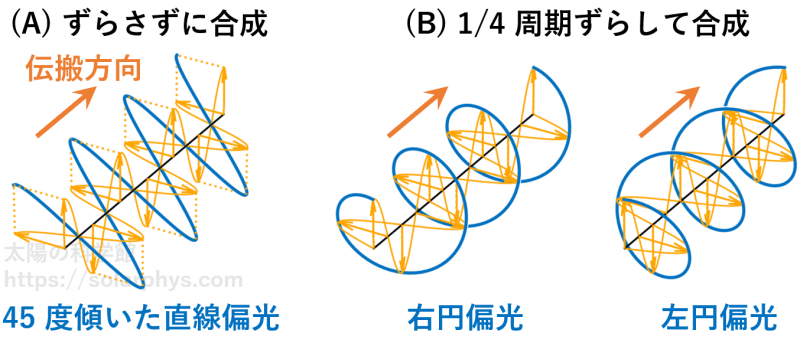
この黄色の 2 つの直線偏光を足し合わせることで作れる偏光状態はこれだけではありません。図 8 (A) では 2 つの直線偏光の振動のタイミング ( = 位相) を一致させて重ねました。一方で、位相を 1/4 周期分だけずらして重ね合わせると、図 8 (B) のように、グルグルと螺旋を描くような偏光状態が得られます。これを円偏光と言います。
前後のどちらにずらすかによって、左巻きの螺旋か右巻きの螺旋かに分かれます。図ではそれぞれ「右円偏光」「左円偏光」と名付けていますが、どちらを左/右と呼ぶかについては、研究分野によってまちまちであるため、注意が必要です。
図 8 (A) の黄色の直線偏光の片方を 1/2 周期分だけずらして重ねると、(A) とは反対側に 45 度傾いた直線偏光が得られます。ここまでの説明がイメージしやすくなるように、位相を様々にずらして重ね合わせた結果を回転させた動画を 図 9 に示します。
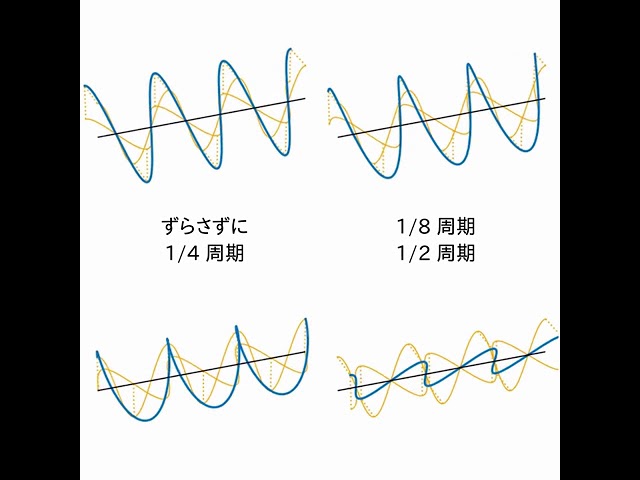
図 4 で紹介した C-PL フィルターは 2 つのフィルムが重なったものです。 1 つは偏光板、もう 1 つは 1/4 波長板と呼ばれるものです。1/4 波長板とは、直線偏光を円偏光に変換して透過することができる装置です。C-PL フィルターに無偏光を通した場合、図 10 のような変換経路を辿ります。
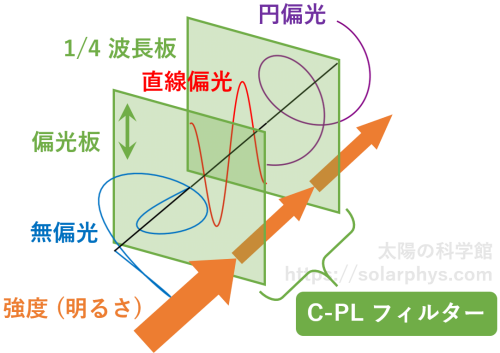
入射した無偏光は初めに偏光板に通され、透過軸方向の直線偏光成分だけが抽出されます。その直線偏光は続いて 1/4 波長板に通されることで、円偏光に変換されます。
パソコン画面の光 (水平に直線偏光) を C-PL フィルターに通した場合、図 11 のようになります。C-PL フィルター内の偏光板の透過軸 (図の矢印) が画面の直線偏光と直交する場合は、初めの偏光板で完全に遮断されます。一方で、両者の向きが一致すれば、(理想的には) 完全に透過されます。
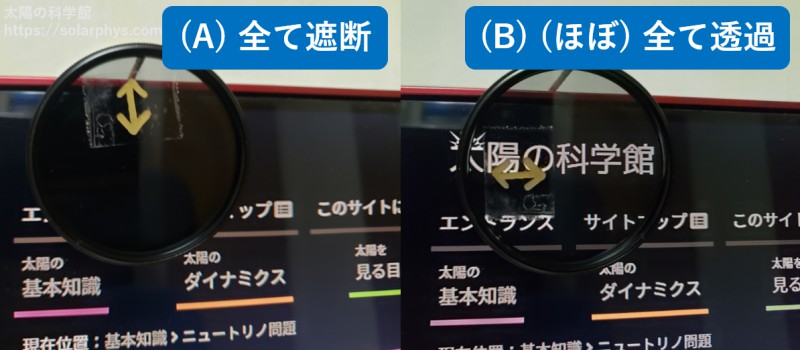
パソコン画面の光を C-PL フィルターに通してから、更に偏光板にも通したときの様子が 図 12 です。注目すべきは (A) です。手前の偏光板の透過軸は鉛直なので、当然画面は基本的に見えなくなっていますが、C-PL フィルター越しの画面だけは見ることができます。これは、C-PL フィルターから出てくる光が円偏光の状態にあるためです。

上述したように、円偏光は直交する等しい強度の 2 つの直線偏光を (位相をずらして) 足し合わせたものと解釈できます。このうち、手前にある偏光板の透過軸方向の成分のみが透過されて、カメラまで届いているわけです。図で C-PL フィルター & 偏光板越しに見ている画面は、(A)、(B) のどちらの場合も、(理想的には) 元の画面の 1/2 の明るさになっています。
2 種類の意味での「重ね合わせ」
直線偏光や円偏光は、直交する 2 つの直線偏光に分解して解釈できることを述べました。一方で、例えば 2 つの電灯と偏光板を使って、\(x\) 方向と \(y\) 方向の直線偏光 (両者とも強度 1 ) を独立に用意し、その 2 つの光線を 1 つにまとめることができたとします ( 図 13 )。このとき、生成された強度 2 の光線は無偏光になります。
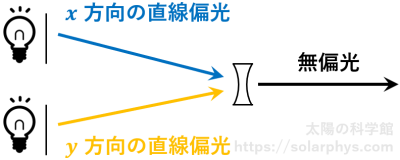
用意した 2 つの直線偏光の位相のずれによって、生成される光線の偏光状態は直線偏光になったり円偏光になったりするのではないか?という考えを持たれた方もいるかもしれません。この考えは全くの間違いではありません。
光子の集合としての光線
普通の電灯が発する光は、電灯を構成するたくさんの原子や分子の運動状態が変化する際に、それぞれ勝手に発せられた光の集合です。それぞれの放出反応では、例えば \(10^{-8} \ \text{s}\) のようなとても短い間だけ光を発します。その短い光ひとつひとつを光子と呼びます。光子がたくさん寄せ集まったものを我々は目にしているわけです ( 図 14 )。
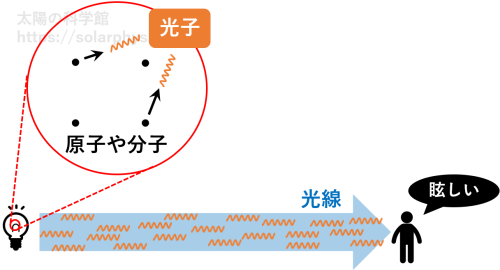
各反応で発せられた光子はそれぞれ勝手な位相を持っているため、用意した各直線偏光はランダムに変化する位相を持っています。このため、重ね合わされた光は、様々な偏光状態がランダムに入り混じった状態になります。そのような状態を無偏光と言うのでした。
発せられる光子の位相や波長がきちんと整っていて、上に載せた図に描かれているような正弦波がずっと続くような状態の光を「コヒーレント光」と言います。そのような光を作るにはそれ相応の技術が必要です。例えばレーザーがその例です。物を照らすための電灯には、通常そのような技術は組み込まれていません。
波的な重ね合わせと統計的な重ね合わせ
このように、我々が観察することのできる光線を考える場合には、次の 2 つの意味での「重ね合わせ」を区別する必要があります。
- 偏光状態の位相のずれを規定したうえでの波としての重ね合わせ
- 光線を光子の集合と考えたときの統計的な意味での重ね合わせ
例えば、\(x\) 軸に対して 60 度傾いた直線偏光を、透過軸を \(x\) 方向に向けた偏光板に通した場合、透過した光線は \(x\) 軸方向に直線偏光しています ( 図 15 )。これは 60 度傾いた直線偏光が、\(x\) 方向と \(y\) 方向の直線偏光を重ね合わせたものと解釈できるからでした。このときの「重ね合わせ」の意味は上記の 1 にあたります。
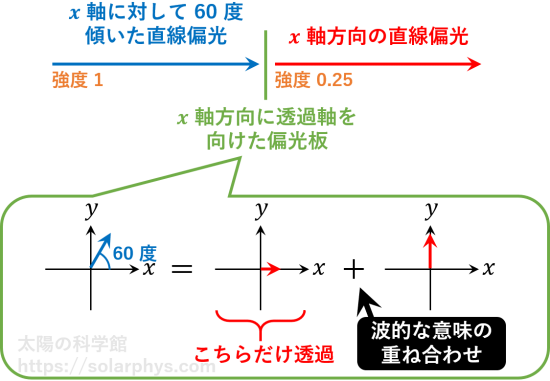
60 度傾いたベクトルが含む \(x\) 成分と \(y\) 成分の比率は \(1 : \sqrt{3}\) です。波的な重ね合わせでは、波の振幅についてベクトル的な分解ができます。光の強度は振幅の 2 乗に比例するため、 図 16 の計算より、得られる \(x\) 偏光の強度は元の 1/4 であると分かります。ただし、理想的な実験を行えばの話です。

一方で、無偏光の光線に対して、 \(x\) 方向に透過軸を向けた偏光板をかざした場合、\(x\) 方向の直線偏光が得られ、その強度は元の半分となります ( 図 17 )。これは、無偏光の光線が、互いに直交する向きの直線偏光を等しい強度で重ね合わせたものと解釈できるからです。このときの「重ね合わせ」は上記の 2 にあたります。
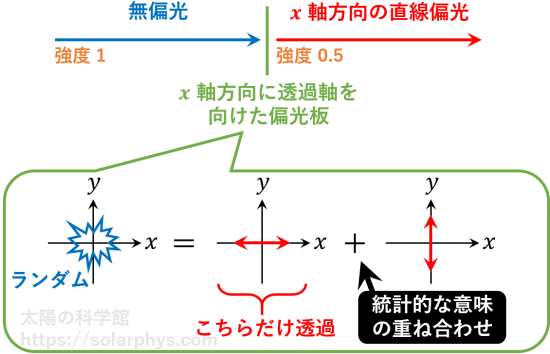
無偏光を 2 つの偏光状態の統計的重ね合わせで表す方法は 1 通りだけではありません。分解した 2 つの状態が直交関係にあり、等しい強度なら何でも良いのです。つまり、例えば \(x\) 軸に対して 60 度傾いた直線偏光と -30 度傾いた直線偏光の統計的重ね合わせとも解釈できます ( 図 18 )。このため、偏光板の透過軸をどの向きに設定しても透過される光の強度は元の 1/2 になります。
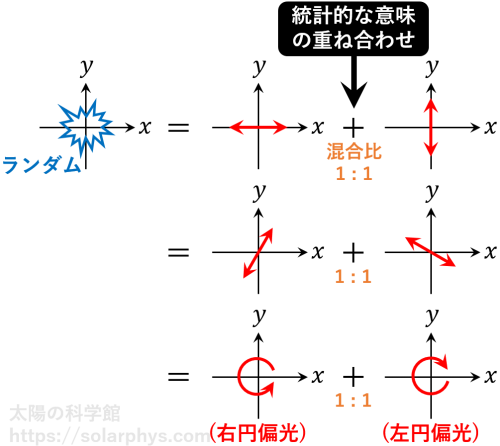
右円偏光と左円偏光もこの意味で「直交関係」にあります。よって、無偏光はこの 2 つの偏光状態の統計的重ね合わせとも解釈できます。例えば偏光板と 1/4 波長板を組み合わせることで、右円偏光だけを透過するようなフィルターを作り、無偏光の光を通したならば、透過光の強度は理想的には元の 1/2 になります。
部分偏光
今までこの記事内で「直線偏光」とか「右円偏光」などと呼んできた光線は、含まれる光子が全てその偏光状態にあるような光線を指します。一方で、「無偏光」とは逆に、含まれる光子の偏光状態がランダムであり、統計的にどの状態にも偏っていないような光線を指します。両者の間には、「統計的にある偏光状態に偏っているけれども、含まれる全ての光子がその状態なわけではない」という光線の状態が存在します。これを「部分偏光」と言います。対して、含まれる全ての光子が同じ偏光状態にあるような光線は「完全偏光」と呼ばれます。
光線の偏光状態に対して、偏光度という指標を考えることができます。偏光度がゼロなのは無偏光の光線です。偏光度が 1 である光線が完全偏光、0 と 1 の間である光線が部分偏光です。
例えば、電灯と偏光板を用いて、\(x\) 軸方向の完全直線偏光と \(y\) 軸方向の完全直線偏光 を独立に用意したとします。前節の例ではこれを等しい強度で重ねた場合を考えましたが、今度は \(x\) 偏光の強度を 3 、\(y\) 偏光の強度を 1 に設定して重ねた場合を考えます。このとき、得られる光線 (強度 4) は統計的に \(x\) 方向の直線偏光に偏った部分偏光であり、その偏光度は 0.5 になります ( 図 19 )。具体的な偏光度の計算方法は下の節で説明します。
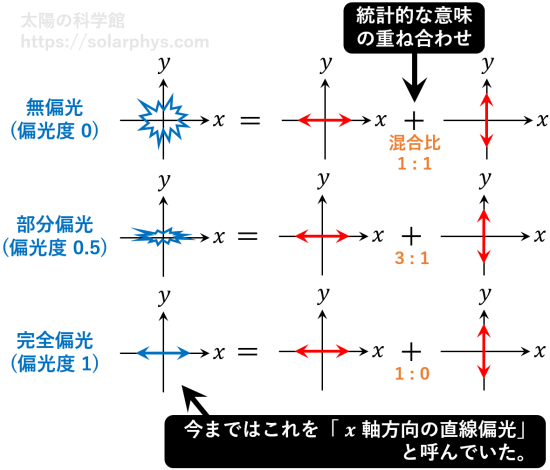
完全偏光の光線に対しては、その光線を完全に透過するようなフィルターを (理想的には) 作ることができます。例えば \(x\) 方向の完全直線偏光に対しては、\(x\) 方向に透過軸を向けた偏光板がそれにあたります。一方で、部分偏光や無偏光の光線に対してはそのようなフィルターを作ることができません。どのようなフィルターを用意しても、そのフィルターに直交する偏光状態を持つ光子を含んでいるからです。これが完全偏光のアイデンティティです。
数学的な記述方法 1 :偏光状態をベクトルで
様々な偏光状態の性質を説明してきました。かなりややこしく感じられたと思います。各完全偏光の状態は他の状態の波的 (ベクトル的) な重ね合わせとして解釈することができるのでした。更に、我々が観測できる光線の状態を考えるには、光線同士の重ね合わせや、部分偏光、無偏光といった統計的な議論もする必要があるのでした。
では、例えば次の 2 つの問いを考えます。
- 等しい強度の右円偏光と左円偏光を波的に合成すると、どのような偏光状態が得られるか?
- 完全な \(x\) 方向の直線偏光と \(y\) 方向の直線偏光の光線を独立に用意し、その 2 つの光線を強度比 3 : 1 で重ねた場合を考える。得られた光線に対して \(x\) 軸から 60 度傾いた透過軸を持つ偏光板をかざしたとき、透過光の強度は理想的にはどうなるか?
想像できない問題に遭遇したときは数式に頼るのがひとつの手段です。偏光状態はベクトルや行列を用いることによって上手く計算することができます。その手法を紹介します。
まずは偏光状態の波的な重ね合わせを考えます。各偏光状態はベクトルに代表させることができます。ただし、 虚数 (複素数) 脚注 [複素数]:\(0.25\) とか \(3\) のような、「普通の数」を実数と言います。ゼロ以外の実数の 2 乗は必ず正の数になります。一方で、2 乗すると負の数になるような数を考えることができます。これを虚数と言います。虚数は虚数単位 \(i\) という数を導入することで、具体的に書き表すことができます。 \(i^2=-1\) です。例えば 2 乗すると \(-9\) になる数は、\(3i, -3i\) の 2 つです。\(2+3i\) のように、実数と虚数が混じった数は複素数と呼ばれます。 も必要になります。\(x\) 方向の直線偏光と \(y\) 方向の直線偏光を表すベクトルをそれぞれ
\[\ket{x}=\begin{pmatrix} 1 \\ 0 \end{pmatrix}, \qquad \ket{y}=\begin{pmatrix} 0 \\ 1 \end{pmatrix}\]
と書くことにします。\(\ket{x}\) はその量がベクトルであることを示すための記号であり、文字の上に書く矢印 \(\vec{x}\) と同じような意味です。私はこの記号が分かりやすいと感じるため、好んで用いています。
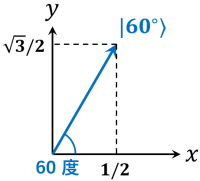
すると、例えば \(x\) 軸に対して 60 度傾いた直線偏光を表すベクトル \(\ket{60^\circ}\) は次のようになります ( 図 20 )。
\[\ket{60^\circ} = \begin{pmatrix} 1/2 \\ \sqrt{3}/2 \end{pmatrix}\]
\(\ket{60^\circ}\) は \(\ket{x}\) と \(\ket{y}\) の和として、
\[\ket{60^\circ} = \frac{1}{2}\ket{x} + \frac{\sqrt{3}}{2}\ket{y}\]
と書けます。右辺の各ベクトルの係数に注目することで、60 度の直線偏光には、\(x\) 偏光と \(y\) 偏光が振幅にして \(1 : \sqrt{3}\) の比率で含まれていることが分かります。すなわち、強度にして \(1^2 : (\sqrt{3})^2 = 1 : 3\) です。
1 つ注意書きとして、今の議論ではベクトルの向きにのみ興味があるので、大きさ (長さ) は常に 1 に設定して考えます。
右円偏光 (R) と左円偏光 (L) を表すベクトルは次のように定義されます。
\[\ket{R} = \begin{pmatrix} -1/\sqrt{2} \\ -i/\sqrt{2} \end{pmatrix}, \qquad \ket{L} = \begin{pmatrix} 1/\sqrt{2} \\ -i/\sqrt{2} \end{pmatrix}\]
虚数単位の混じったベクトルの大きさは次のように考えます。\(\ket{R}\) の縦に並んだ成分を横向きにして、成分が複素数であった場合には 複素共役 脚注 [複素共役]:ある複素数に対して、虚数単位 \(i\) の係数の符号を逆にした数をその複素数の複素共役と言います。例えば \(1+3i\) の複素共役は \(1-3i\) です。 を取ったものを次のように書きます。
\[\bra{R} = \begin{pmatrix} -1/\sqrt{2} & i/\sqrt{2} \end{pmatrix}\]
この \(\bra{R}\) を元の \(\ket{R}\) に左から掛けて行列計算をし、最後にルートを取ったものがベクトルの大きさと定義されます。
\begin{align} \left|\ket{R}\right| &= \sqrt{\braket{R|R}} \\ &= \sqrt{\begin{pmatrix} -1/\sqrt{2} & i/\sqrt{2} \end{pmatrix} \begin{pmatrix} -1/\sqrt{2} \\ -i/\sqrt{2} \end{pmatrix}} \\ &= \sqrt{\left(-\frac{1}{\sqrt{2}}\right)^2 + \frac{i}{\sqrt{2}}\left(-\frac{i}{\sqrt{2}}\right)} \\ &=1 \end{align}
実際に計算すると、上記のように \(\ket{R}, \ket{L}\) の大きさはちゃんと 1 に設定されていることが分かります。\(\ket{R}\) と \(\ket{L}\) の内積とは、次のような量のことを指します。
\begin{align}\braket{R|L} &= \begin{pmatrix}-1/\sqrt{2} & i/\sqrt{2}\end{pmatrix}\begin{pmatrix} 1/\sqrt{2} \\ -i/\sqrt{2}\end{pmatrix} \\ &= 0\end{align}
内積がゼロであることから、右円偏光と左円偏光は直交関係にあることが分かります。
\(\ket{R}\) は \(\ket{x}, \ket{y}\) の重ね合わせとして、
\[\ket{R} = -\frac{1}{\sqrt{2}}\ket{x}-\frac{i}{\sqrt{2}}\ket{y}\]
と書けます。右辺の係数を見ることで、確かに右円偏光が \(x\) 偏光と \(y\) 偏光を強度にして
\[\left(-\frac{1}{\sqrt{2}}\right)^2 : \frac{i}{\sqrt{2}}\left(-\frac{i}{\sqrt{2}}\right) = 1 : 1\]
の比率で波的に重ね合わせたものであることが分かります。重ね合わせるときに位相をずらす操作は、係数に虚数が混じることとして反映されています。
ここまでくると、上述した 1 の問いに答えることができます。例えば、右円偏光と左円偏光の位相をずらさずに等しい強度で波的に重ね合わせた場合を考えたいならば、単純に次の和を考えます。
\begin{align}\frac{1}{\sqrt{2}}\left(\ket{R}+\ket{L}\right) &= \begin{pmatrix} 0 \\ -i \end{pmatrix} \\ &= -i \ket{y}\end{align}
計算結果のベクトルの大きさが 1 になるように、\(1/\sqrt{2}\) を掛けました。計算結果のベクトルは \(\ket{y}\) の向きです。従って、得られる偏光状態は \(y\) 軸方向の直線偏光であることが分かります。あるいは、両者の位相を半波長分ずらして重ね合わせた場合を考えるならば、足し算の代わりに引き算を行うことで、次のように計算できます。
\begin{align}\frac{1}{\sqrt{2}}\left(\ket{R}-\ket{L}\right) &= \begin{pmatrix} -1 \\ 0 \end{pmatrix} \\ &= - \ket{x}\end{align}
つまり、得られる偏光状態は \(x\) 軸方向の直線偏光です。このように、右円偏光と左円偏光を等しい強度で波的に重ね合わせた場合、両者の位相差によって、いずれかの方向の直線偏光が得られます。
数学的な記述方法 2 :光線の統計的状態を行列で
光線の状態は行列に代表させることができます。ベクトルであることを明示するために \(\ket{x}\) という記号を用いたのと同じように、行列であることを示すために \(\hat{\rho}\) という記号を用います。
例えば、\(x\) 軸方向に完全に直線偏光した強度 3 の光線 A を表す行列は次のようになります。
\begin{align} \hat{\rho}_{A} &= 3\cdot\ket{x}\bra{x} \\ &= 3\begin{pmatrix} 1 \\ 0\end{pmatrix}\begin{pmatrix} 1 & 0\end{pmatrix} \\ &= \begin{pmatrix} 3 & 0 \\ 0 & 0\end{pmatrix}\end{align}
\(x\) 方向に完全に直線偏光した強度 1 の光線と、\(y\) 方向に直線偏光した強度 1 の光線を独立に用意して重ねると、強度 2 の無偏光の光線 (B) が得られます。このことを踏まえて、この光線 B を表す行列は次のように書けます。
\begin{align} \hat{\rho}_B &= 1\cdot\ket{x}\bra{x} + 1\cdot\ket{y}\bra{y} \\ &= \begin{pmatrix} 1 \\ 0\end{pmatrix}\begin{pmatrix} 1 & 0\end{pmatrix} + \begin{pmatrix} 0 \\ 1\end{pmatrix}\begin{pmatrix} 0 & 1\end{pmatrix} \\ &=\begin{pmatrix} 1 & 0 \\ 0 & 1\end{pmatrix}\end{align}
もう 1 つ例を示します。完全に右円偏光の状態にある強度 2 の光線 C を表す行列は次のように書けます。
\begin{align} \hat{\rho}_C &= 2\cdot\ket{R}\bra{R} \\ &= 2\begin{pmatrix} -1/\sqrt{2} \\ -i/\sqrt{2} \end{pmatrix}\begin{pmatrix} -1/\sqrt{2} & i/\sqrt{2}\end{pmatrix} \\ &= \begin{pmatrix} 1 & -i \\ i & 1\end{pmatrix} \end{align}
行列の構成ルールは理解していただけたと思います。これらの行列から色々な情報が得られます。例えば光線の強度は、行列の対角要素の和を取ることで調べられます。例えば光線 A, B, C の場合については、それぞれ 図 21 のように計算できます。
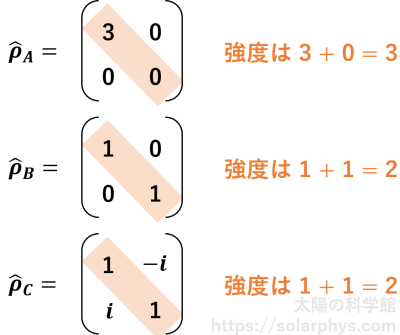
無偏光は、上述したように、完全な右円偏光と左円偏光を独立に用意して重ねることによっても得られるのでした。このことに関連して、\(\hat{\rho}_B\) は次のようにも分解できます。
\begin{align}\hat{\rho}_B &= \begin{pmatrix}1 & 0 \\ 0 & 1\end{pmatrix} \\ &=\begin{pmatrix} 1/2 & -i/2 \\ i/2 & 1/2\end{pmatrix}+\begin{pmatrix} 1/2 & i/2 \\ -i/2 & 1/2\end{pmatrix} \\ &= \begin{pmatrix} -1/\sqrt{2} \\ -i/\sqrt{2}\end{pmatrix}\begin{pmatrix}-1/\sqrt{2} & i/\sqrt{2}\end{pmatrix}+\begin{pmatrix} 1/\sqrt{2} \\ -i\sqrt{2}\end{pmatrix}\begin{pmatrix} 1/\sqrt{2} & i/\sqrt{2}\end{pmatrix} \\ &= 1\cdot\ket{R}\bra{R} + 1\cdot\ket{L}\bra{L}\end{align}
光線に何らかのフィルターをかざしたときに透過する光の強度を調べたい場合は、次のように考えます。例えば光線 C (強度 2 の右円偏光) に \(x\) 方向の直線偏光のみ透過する偏光板をかざした場合、
\begin{align}\braket{x|\hat{\rho}_C|x} &=\begin{pmatrix} 1 & 0 \end{pmatrix}\begin{pmatrix} 1 & -i \\ i & 1\end{pmatrix}\begin{pmatrix} 1 \\ 0 \end{pmatrix} \\ &= 1\end{align}
と計算することで、透過される光の強度は 1 であることが分かります。
ここまでくると、上の節で述べた 2 の問いにも答えることができます。再掲すると、次の問いです。
- 完全な \(x\) 方向の直線偏光と \(y\) 方向の直線偏光の光線を独立に用意し、その 2 つの光線を強度比 3 : 1 で重ねた場合を考える。得られた光線に対して \(x\) 軸から 60 度傾いた透過軸を持つ偏光板をかざしたとき、透過光の強度は理想的にはどうなるか?
2 つの光線を重ねて得られる強度 4 の光線 (D) を表す行列は次のように書けます。
\begin{align}\hat{\rho}_D &= 3\cdot\ket{x}\bra{x}+1\cdot\ket{y}\bra{y} \\ &= \begin{pmatrix} 3 & 0 \\ 0 & 1\end{pmatrix}\end{align}
よって、問いの偏光板をかざしたときに得られる強度は次のように計算できます。
\begin{align}\braket{60^\circ|\hat{\rho}_D|60^\circ} &= \begin{pmatrix} 1/2 & \sqrt{3}/2\end{pmatrix}\begin{pmatrix} 3 & 0 \\ 0 & 1\end{pmatrix}\begin{pmatrix} 1/2 \\ \sqrt{3}/2\end{pmatrix} \\ &= 1.5\end{align}
数学的な記述方法 3 :ストークスパラメータ
光線を表す行列の成分を
\[\hat{\rho} = \frac{1}{2}\begin{pmatrix} I+Q & U-iV \\ U+iV & I-Q\end{pmatrix}\]
と表したときの実数 \(I,Q,U,V\) をストークスパラメータと言います。行列が与えられれば \((I,Q,U,V)\) の組が計算でき、逆に \((I,Q,U,V)\) の組が与えられればそこから行列が得られるため、行列の代わりにストークスパラメータを用いることでも、光線の偏光状態を表すことができます。
天文学の分野ではストークスパラメータがよく用いられます。それは、ストークスパラメータが光の観測から得られる情報に即しているからです。ストークスパラメータはそれぞれ次の意味を持っています。
- \(I\) は光線の強度を表す。
- \(x\) 方向の直線偏光を透過するフィルターをかざしたときの透過光強度を \(I_x\)、\(y\) 方向の直線偏光を透過するフィルターをかざしたときの透過光強度を \(I_y\) としたとき、\(Q=I_x-I_y\) である。
- \(x\) 軸から \(y\) 軸の方に 45 度傾いた直線偏光を透過するフィルターをかざしたときの透過光強度を \(I_{45}\)、135 度傾いた直線偏光を透過するフィルターをかざしたときの透過光強度を \(I_{135}\) としたとき、\(U=I_{45}-I_{135}\) である。
- 右円偏光を透過するフィルターをかざしたときの透過光強度を \(I_R\)、左円偏光を透過するフィルターをかざしたときの透過光強度を \(I_L\) としたとき、\(V=I_R-I_L\) である。
例えば上の節の光線 C (完全な右円偏光) の場合、\((I,Q,U,V)=(2,0,0,2)\) であり、光線 D の場合は \((I,Q,U,V)=(4,2,0,0)\) です。ただし、右円偏光と左円偏光を逆に定義している文献の場合は、\(V\) は上の定義とは逆符号になっている可能性があります。
ストークスパラメータを用いて次のように計算される \(p\) を偏光度と言います。
\[p = \frac{\sqrt{Q^2+U^2+V^2}}{I}\]
例えば光線 C の場合は \(p=1\)、光線 D の場合は \(p= 0.5\) です。既に述べたように、\(p\) がとり得る値の範囲は \(0 \le p \le 1\) であり、\(p=0\) の場合は無偏光、\(p=1\) の場合は完全偏光、それ以外の場合は部分偏光にあたります。
参考文献
記事全体として参考にした書籍
- del Toro Iniesta, J. C. (2003). Introduction to Spectropolarimetry (Cambridge: Cambridge University Press ).
- Blum, K. (2012). Density Matrix Theory and Applications (Berlin: Springer ).