太陽表面の模様
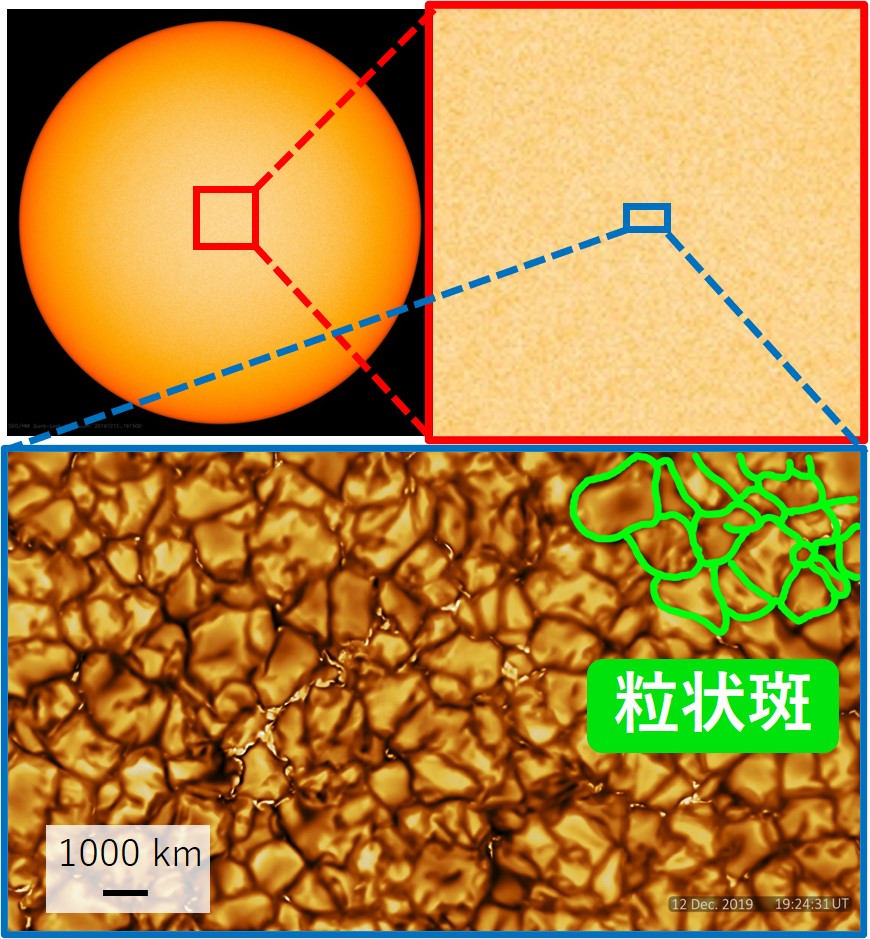
太陽表面のうちの黒点以外の部分は、太陽全体の画像を見た限りではのっぺりと無模様に見えます。しかし、拡大して見ると、図 1 のように細胞状の構造がたくさん並んだような模様が見えます ( 図の色について 脚注 [図の色]:図に映っている太陽の色は人工的に着けられたものです。惑わされないでください。これらの図は、特定の波長の光だけを通すフィルターを付けた望遠鏡によって撮影されたものであり、要はモノクロ画像です。得られた光の強度を慣習に従った色によって図示しています。 )。この構造のひとつひとつを粒状斑 (granule) と言います。
 :提供 NSO/NSF/AURA, licenced under CC BY 4.0 , 元動画 (全体) 赤枠と青枠は太陽全体に対するスケールを示すためのものであり、DKIST が太陽表面のうちのどの部分を撮影したかを表しているわけではない。
:提供 NSO/NSF/AURA, licenced under CC BY 4.0 , 元動画 (全体) 赤枠と青枠は太陽全体に対するスケールを示すためのものであり、DKIST が太陽表面のうちのどの部分を撮影したかを表しているわけではない。
粒状斑の大きさは典型的には 1000 km 程度です。これは大体日本の本州くらいの大きさです。図 2 に 図 1 の動画版を載せます。ハワイにある米国の太陽望遠鏡 DKIST が捉えた太陽表面です。現実の 10 分間にあたる映像が繰り返されています。
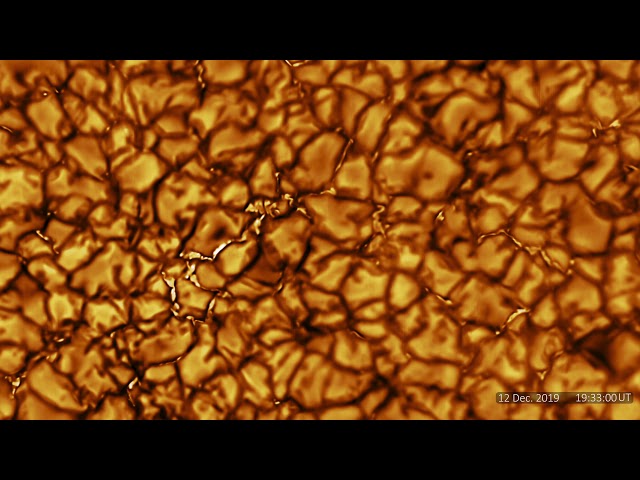
動画を見ると、各々の粒状半は新たに生まれたり、小さくなって消滅したり、分裂したりと、数分の時間スケールで様子が変化していきます。
上の動画は地球から円盤状に見える太陽の中央付近を拡大して写したものです。つまり、太陽表面を真上から見ています。一方で、米国の太陽望遠鏡 GST が太陽円盤の縁付近を捉えた動画を 図 3 に載せます。こちらでは、太陽表面を斜め上から見ていることになります。図 2 よりも広範囲が写っています。

動画を見ると、やはり黒点以外の領域では粒々模様が数分の時間スケールで絶えず変化しています。このように、
光球
脚注
[光球]:フィルターを通さずに可視光で観測したときに明るく映る層のことです。大雑把にはこの層が「太陽表面」と呼ばれます。より細かくは高度 0 から 500 km あたりの層を言います。
 (太陽表面) を観測した場合、粒状斑は黒点以外の全領域に渡って見られます。
(太陽表面) を観測した場合、粒状斑は黒点以外の全領域に渡って見られます。
図 3 では、所々に明るい領域が見えます。これを白斑 (facula) と言います。図 3 に写っている白斑の一部を拡大して 図 4 に示しました。
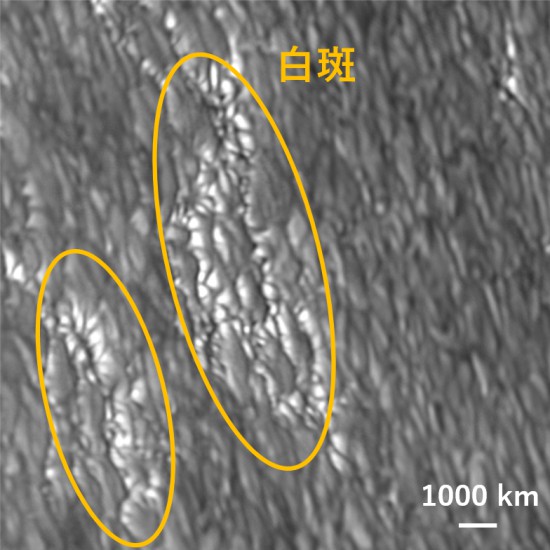
この白斑領域は丘のように出っ張った構造をしている (逆に言うと粒状斑と別の粒状斑の間が谷になっている) ようにも見えます。白斑について詳しくは下の節で説明します。
粒状斑とは何か?
粒状斑は太陽表面で起きている
熱対流
脚注
[熱対流]:水の入った鍋を下からコンロで熱すると、熱くなった底付近の水は軽くなって上方へ移動します。逆に元々鍋の上方にあった水は熱せられた水と比べて重いため、下方へ移動します。これの繰り返しによって、鍋の中の水は温度を一様にしようとします。これが熱対流です。エネルギーの観点では、下からコンロによって加えられる熱エネルギーを熱対流が上方へ輸送していることになります。
 の様子です。お椀に味噌汁を注いで暫く経つと、まだら模様が見えてきます。これは味噌汁の水面が冷やされることで熱対流が起きているからです。味噌汁の場合は液体、太陽表面の場合は気体という違いはありますが、粒状斑も基本的にはこれと同じ類の現象です。
の様子です。お椀に味噌汁を注いで暫く経つと、まだら模様が見えてきます。これは味噌汁の水面が冷やされることで熱対流が起きているからです。味噌汁の場合は液体、太陽表面の場合は気体という違いはありますが、粒状斑も基本的にはこれと同じ類の現象です。
シミュレーション
粒状斑はコンピュータシミュレーションによって上手く再現されています。図 5 はコンピュータ上に太陽表面付近を模した 3 次元の箱を用意し、その中で 磁気流体力学 脚注 [磁気流体力学]:液体や十分に濃い気体の速度、温度、圧力や密度などの時間発展を計算するための理論を流体力学と言います。特に、プラズマのような電気を通す流体を記述するために、流体力学と電磁気学を融合させた理論を磁気流体力学 (MHD) と言います。 と 放射輸送理論 脚注 [放射輸送]:太陽を構成するプラズマは高温なので、通常の熱伝導や熱対流に加えて、光を放出したり、近くで放出された光を吸収したりすることによって運ばれるエネルギーも無視することができません。これを放射輸送と言います。周りの物質分布や温度などの情報から、各場所での光の強度を計算するための方程式を放射輸送方程式と言います。 の方程式を解くことによって計算された粒状斑の様子です。仮に真上から観測したときにどのように見えるのかが示されています。

詳しくは記事「プラズマ診断:太陽を「見る」だけでここまで分かる」で説明していますが、太陽スペクトルに現れる
吸収線
脚注
[吸収線]:太陽からの光をスペクトル分解 ( = 各波長ごとの強度を表示) すると、周りと比べて強度の弱い波長帯が所々に現れます。これを吸収線と言います。逆に、どの吸収線にも該当しないような波長の光を連続光と言います。
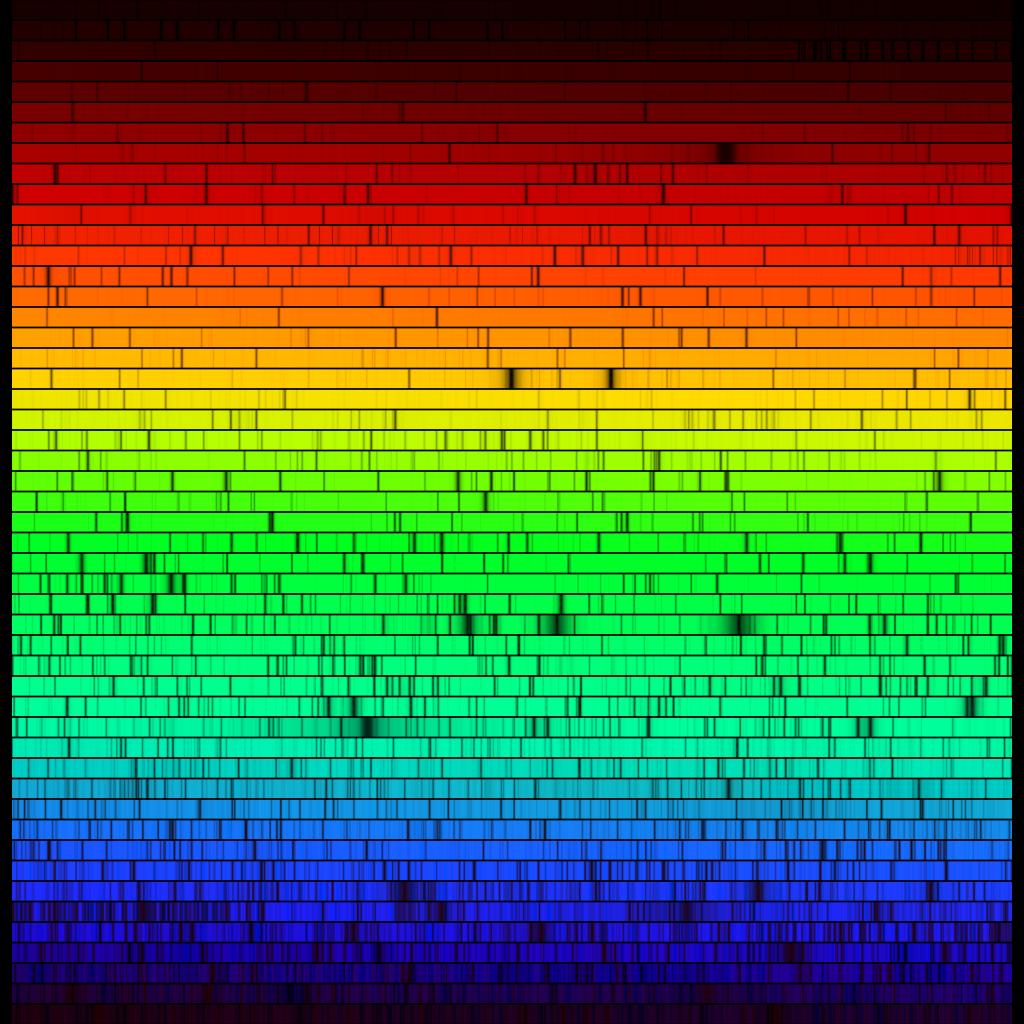 図:太陽光を各波長 (色) ごとに分解したもの。黒く見える波長が吸収線。提供 N.A.Sharp, NOAO/NSO/Kitt Peak FTS/AURA/NSF
の中には太陽表面での気体の温度や動きによってその深さや形が変化するものがあります。上述したようなシミュレーションで再現された吸収線の深さや形は、実際に観測されるものと一致します。また、上の動画で示されている粒状斑の様子は、前節で示した観測結果 (特に白斑領域) と良く似ています。このことから、シミュレーションは正しく粒状斑を再現できていると考えられています ( 例えば Nordlund et al., 2009 )。
図:太陽光を各波長 (色) ごとに分解したもの。黒く見える波長が吸収線。提供 N.A.Sharp, NOAO/NSO/Kitt Peak FTS/AURA/NSF
の中には太陽表面での気体の温度や動きによってその深さや形が変化するものがあります。上述したようなシミュレーションで再現された吸収線の深さや形は、実際に観測されるものと一致します。また、上の動画で示されている粒状斑の様子は、前節で示した観測結果 (特に白斑領域) と良く似ています。このことから、シミュレーションは正しく粒状斑を再現できていると考えられています ( 例えば Nordlund et al., 2009 )。
シミュレーション結果の解析から、粒状斑の物理については詳しく分かっています。
熱対流の仕組み
太陽表面では、エネルギーが光として常に宇宙空間に逃げて行きます ( 図 6 )。このエネルギー損失によって表面は強く冷やされます。冷やされた気体は収縮し、周囲より重くなるため、重力に従って下降します。その下降流を補うようにして、周りの暖かくて軽い気体は上昇します。これが粒状斑の熱対流の基本的な仕組みです。

内部から浮力によって表面に上昇してくる気体の温度は 1 万 K ( ケルビン 脚注 [ケルビン]:温度の単位には基本的にケルビン (K) を用います。日常で使われる摂氏と目盛の幅は同じであり,摂氏 0 度は 273.15 K です。つまり,例えば 300 K は摂氏 26.85 度のことです。 ) 程度です。これが 図 2 で明るい粒状斑として見えている領域に相当します。上昇してきた気体は 6000 K 程度まで冷やされて重くなり、下降流に転じます。これが 図 2 で見られる粒状斑と粒状斑の間の暗い領域に相当します。
見えている高度
図 7 に先ほど示したシミュレーション結果のスナップショット (ある時刻での様子) を載せました。図に白色で示した線分で切った時の鉛直面内の様子を 図 8 に示します。図 8 の色は温度、矢印は流速の様子を表しています。

図 8 を見ると、確かにシミュレーション内に再現された粒状斑内部には上昇流が存在し、粒状斑と粒状斑の間には下降流が存在しています。流速は \(1 \ \text{km/s}\) の桁数です。下降流は約 6000 K の比較的低温の気体を内部に引き込んでいます。
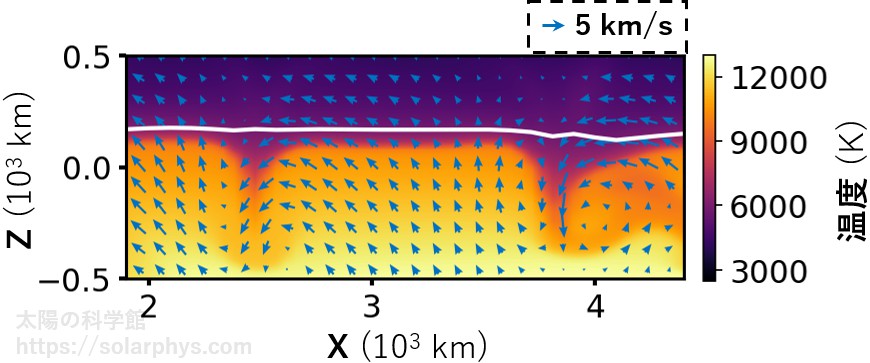
仮に真上から (
連続光
脚注
[連続光]:太陽からの光をスペクトル分解 ( = 各波長ごとの強度を表示) すると、周りと比べて強度の弱い波長帯が所々に現れます。これを吸収線と言います。逆に、どの吸収線にも該当しないような波長の光を連続光と言います。
 図:太陽光を各波長 (色) ごとに分解したもの。黒く見える波長が吸収線。提供 N.A.Sharp, NOAO/NSO/Kitt Peak FTS/AURA/NSF
で) 観測した場合に表面として見える高度を図に白線で示しました。太陽表面を構成する気体は温度によって不透明度が大きく変化します。不透明とは発せられた光が直ぐに隣の部分に吸収されてしまうことであり、透明とは発せられた光がその後吸収されないことを言います。約 6000 K を境に、高温ならば不透明、低温ならば透明になります ( 図 9 )。
図:太陽光を各波長 (色) ごとに分解したもの。黒く見える波長が吸収線。提供 N.A.Sharp, NOAO/NSO/Kitt Peak FTS/AURA/NSF
で) 観測した場合に表面として見える高度を図に白線で示しました。太陽表面を構成する気体は温度によって不透明度が大きく変化します。不透明とは発せられた光が直ぐに隣の部分に吸収されてしまうことであり、透明とは発せられた光がその後吸収されないことを言います。約 6000 K を境に、高温ならば不透明、低温ならば透明になります ( 図 9 )。

内部から上昇してきた 1 万 K の気体は、表面で 6000 K 弱の温度まで急激に冷やされ、一部は透明になります。我々は透明になるかならないかの瀬戸際の約 6000 K の気体を「表面」として認識することになります。
もっと細かい話をすると、下降流の存在する領域では上昇流が存在する領域よりも若干低い温度の気体が表面として見えます。太陽表面を構成する気体は 黒体放射 脚注 [黒体放射]:十分に濃い物質は熱くなると光を放出します。これを熱放射と言います。特に太陽表面のような不透明な物質は熱放射の中でも黒体放射と呼ばれる光り方をします。黒体放射をする物質は温度が高いほど明るく光ります。表面の単位面積から光として失うエネルギー量は温度の 4 乗に比例します (シュテファン-ボルツマンの法則)。 によって光っているため、温度が低いほど暗くなります。このため、上昇流域は明るい粒状斑、下降流域は粒状斑の間の暗い部分として写ります。具体的な温度を挙げると、例えば波長 500 nm の光 (青に近い緑色) で観測した場合、粒状斑の内側では 6500 K 程度、粒状斑と粒状斑の間では 6000 K 程度の気体が見えます ( 例えば Kianfar et al., 2020 )。見える高度は観測する波長によっても違います。
黒体放射について詳しくは記事「黒体放射:なぜ明るいのか?」で説明しています。
謎の超粒状斑
粒状斑は太陽表面に存在する 1000 km のスケールの熱対流であると述べました。太陽表面にはもっと大きなスケールの対流も存在することが分かっています。超粒状斑 (supergranulation) と呼ばれる現象です。
粒状斑は数分で目まぐるしく様子が変化する現象ですが、超粒状斑は 1 日程度の時間スケールの現象であり、粒状斑のように上昇流域と下降流域の明るさのコントラストが明確にあるわけでもないので、太陽表面の明るさの動画を眺めただけではよく分かりません。超粒状斑の姿を確認する方法はいくつかありますが、いちばん直接的な方法は太陽表面での流速の様子を調べることです。
超粒状斑の姿
図 10 は NASA が開発した観測衛星 SDO に搭載された装置 HMI が捉えた
光球
脚注
[光球]:フィルターを通さずに可視光で観測したときに明るく映る層のことです。大雑把にはこの層が「太陽表面」と呼ばれます。より細かくは高度 0 から 500 km あたりの層を言います。
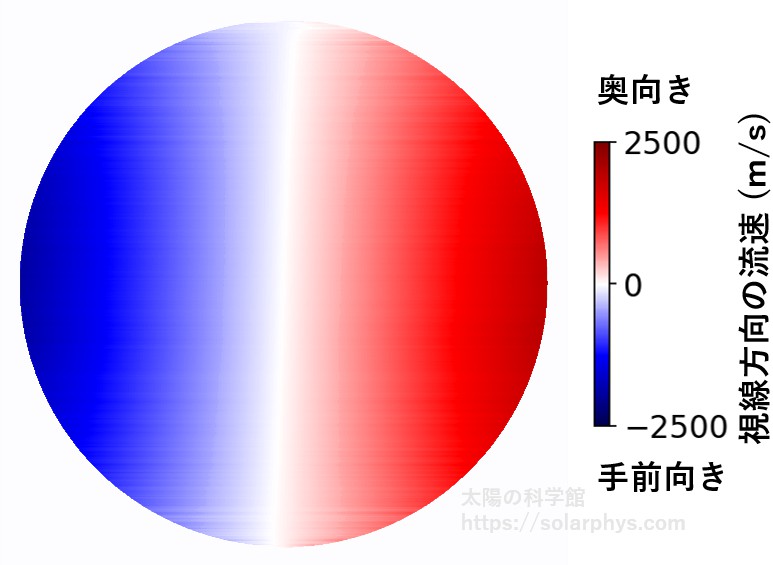
 における視線速度の様子です。視線速度とは、光球の気体が観測機に近づく向き (手前向き) に流速を持つか、遠ざかる向き (奥向き) に持つかです。奥向きが赤、手前向きが青で示されています。ただし、地球の周りを回る観測機が観測時に太陽に近づく向きに速度を持っていたことによる効果はできる限り取り除かれています。どのようにして視線速度を観測するかについては プラズマ診断 の記事で説明しています。
における視線速度の様子です。視線速度とは、光球の気体が観測機に近づく向き (手前向き) に流速を持つか、遠ざかる向き (奥向き) に持つかです。奥向きが赤、手前向きが青で示されています。ただし、地球の周りを回る観測機が観測時に太陽に近づく向きに速度を持っていたことによる効果はできる限り取り除かれています。どのようにして視線速度を観測するかについては プラズマ診断 の記事で説明しています。
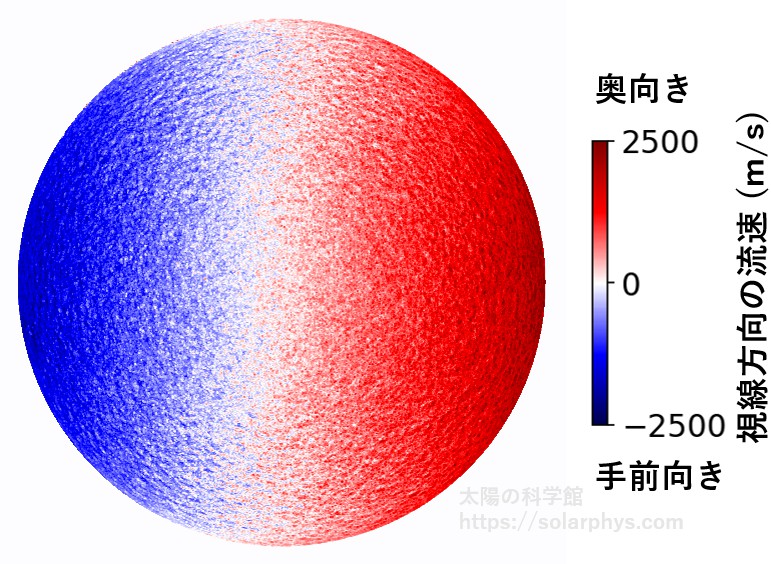
 での視線速度の様子:2015 年 10 月 14 日 0 時 16 分に観測された。生データから全面に対して均一に \(2350 \ \text{m/s}\) 引いた。流速の原点は太陽面の中央付近の視線速度は小さいであろうという仮定の下に目視によって選んだものなので、最大で数百 \(\text{m/s}\) の誤差を含むことに注意してほしい。提供 NASA/SDO and the AIA, EVE, and HMI science teams.
での視線速度の様子:2015 年 10 月 14 日 0 時 16 分に観測された。生データから全面に対して均一に \(2350 \ \text{m/s}\) 引いた。流速の原点は太陽面の中央付近の視線速度は小さいであろうという仮定の下に目視によって選んだものなので、最大で数百 \(\text{m/s}\) の誤差を含むことに注意してほしい。提供 NASA/SDO and the AIA, EVE, and HMI science teams.
図を見ると、太陽面の左半分が青、右半分が赤という大域的な成分が確認できます。これは太陽が図の右向きに自転していることによる効果です (図は自転軸が上下を向くように調整されています)。図の中には超粒状斑による気体の動きの効果も含まれているはずですが、自転のように、他の成分も混ざっているため、それらを除去していくことにします。
記事「太陽内部を探る日震学」で説明しますが、太陽表面には 5 分振動 (5-minute oscillation) と呼ばれる気体の動きも存在します。これは 3 から 15 分程度の周期で振動する現象です。また、粒状斑対流による気体の動きの変化も含まれていることが期待されます。これらの成分は長い時間で平均することによって除去できます。図 10 の前後 33 分間のデータで平均を取ったものが 図 11 です。
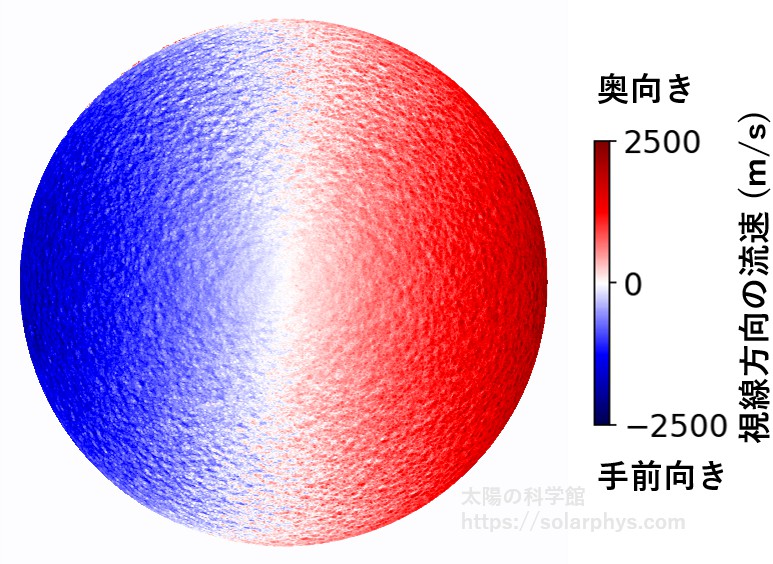
更に、地球から見える太陽の回転 ( = 太陽の自転 + 観測衛星の太陽周りの公転) の効果を上の図から 図 12 のように見積もり、それを除去したものが 図 13 です。
図 13 を見ると、粒状のまだら模様が確認できます。これが超粒状斑による気体の流れの様子です。粒の大きさは典型的には 3 万 km (粒状斑数十個分) です。粒の様子は 1 日程度の時間スケールで変化していきます。太陽面の中央に近づくほどまだら模様のコントラストが薄くなっています。これは、超粒状斑による流れが主に水平方向であることを意味しています。鉛直方向の流れが小さいため、真上から見ると視線速度が小さいわけです。
超粒状斑の起源の謎
このように、太陽表面は主に 2 つのスケールの成分から成る対流をしています ( 図 14 )。粒状斑対流の方は上述したように、コンピュータシミュレーションによって上手く再現されています。一方で、超粒状斑の起源はまだよく分かっていません。

粒状斑についての素朴な考察をしてみます。まず、太陽表面から単位時間・単位面積あたりに光として流出するエネルギー量は、地球で受け取る太陽光の観測から \(6\times 10^7 \ \text{W/m}^2\) と分かっています。
対して、粒状斑対流が太陽内部から表面に運んでくるエネルギー量を見積もってみます。熱力学と流体力学の知識を用いると、気体の熱対流によって単位時間・単位面積あたりに上向きに運ばれる熱量 (エンタルピーフラックス、単位 \(\text{W/m}^2\)) は次のように見積もられます。記号「\(\approx\)」はおよそ等しいという意味で用います。
\begin{align}F &\approx \frac{\gamma}{\gamma-1} n k_B\Delta T v \\ \text{ただし}, \quad \gamma &: \text{比熱比} \\ n &: \text{物質の数密度 [個/m}^3\text{]} \\ k_B &= 1.38 \times 10^{-23} \ \text{J K}^{-1} \\ &: \text{ボルツマン定数} \\ \Delta T &: \text{上昇流と下降流の温度差 [K]} \\ v &: \text{典型的な流速 [m/s]} \end{align}
熱い上昇流と冷たい下降流の温度差が大きいほど、正味として多くの熱量を上に運ぶことになるため、上式は \(\Delta T\) に比例します。また、内部から運ばれてくる熱い物質の量が多いほど効率が良いため、\(n\) や \(v\) にも比例します。
上式に太陽表面での値
\begin{align} \gamma &\approx \frac{5}{3} \\ n &\approx 1 \times 10^{23} \ \text{個/m}^3 \end{align}
と粒状斑対流における値として例えば
\begin{align} v &\approx 3000 \ \text{m/s} \\ \Delta T &\approx 6000 \ \text{K} \end{align}
を代入すると、\(F \approx 6\times 10^7 \ \text{W/m}^2\) となり、表面が光として失うエネルギー量と概ね一致します。つまり、太陽が表面から失うエネルギーは粒状斑対流によって内部から運ばれています。
一方で、超粒状斑対流は粒状斑対流よりも流速が遅いです。また、温度差も小さいと考えられています。例えば Langfellner et al. (2016) によると、表面における超粒状斑の中央と縁での温度差は \(1 \ \text{K}\) 程度のようです。従って、超粒状斑対流は熱輸送には大して寄与していないと思われます。別に超粒状斑が存在しなくとも、太陽表面での熱収支は上手くいくのです。
このため、対流の起源が粒状斑対流と同じ熱的なもの (浮力によるもの) なのか、或いは記事「差動回転:回り方がおかしい?」で説明している差動回転の副産物なのか、はたまた磁場が関係しているのかなど、様々な可能性が考えられてきました。
近年のコンピュータの発達に伴って、より大きな領域における熱対流のシミュレーションが可能になってくると、太陽表面での熱対流は今まで考えられていたよりも複雑な現象であることが見えてきました。近年では、超粒状斑対流も表面付近で起こる熱対流 (浮力による対流) なのではないかという見方が強まっています。
しかし、何が超粒状斑の大きさ (約 3 万 km) を決めているのか?なぜそれよりも大きな熱対流が存在しないのか?なぜ超粒状斑対流の温度差は小さいのか (太陽表面の下でも小さいのか) ?という疑問に答えることはまだできていません。
超粒状斑の謎については 差動回転の記事 でも言及しています。この話題についてより詳しくは、例えば Rincon & Rieutord (2018) を読んでください。
白斑とは何か?
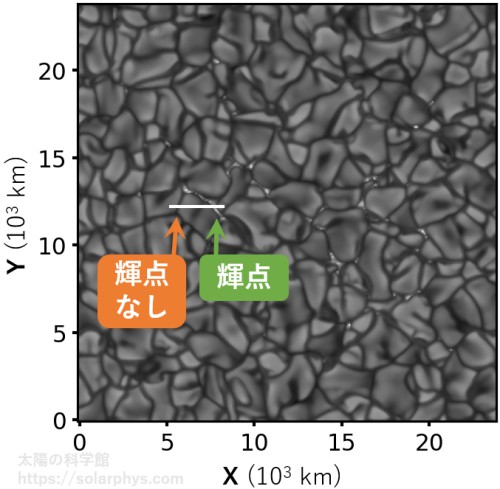
図 4 と同じものを 図 15 に示します。図で明るく写っている領域を白斑と呼ぶのでした。白斑が形成されている領域を真上から観測すると、大抵は 図 16 に写っているように粒状斑と粒状斑の間に掃き集められたアクのような構造が見えます。これを輝点 (bright point) と言います。粒状斑の間の領域は普通は暗いはずなのに、輝点は明るく光っています。

輝点は上述したシミュレーションでも再現されています。図 17 に記した白い線分で切り取ったときの鉛直面内の様子を 図 18 に示します。輝点が形成されている下降流域と輝点のない下降流域が写っている領域を選びました。
輝点 (白斑) = 磁場の強い領域
図 18 の色は、上段からそれぞれ温度、質量密度、磁場の強さを表しています。図を見ると、輝点がある方の下降流域には強い磁場が存在していることが分かります。このことは一般に言えます。実際の輝点を観測した場合の (表面付近の高度での) 磁場強度は \(0.1\) から \(0.2 \ \text{T}\) (
テスラ
脚注
[テスラ]:磁場の強さを表す単位です。理想的には磁力線の密集度に相当しますが、実際の図では特徴的な磁力線だけを間引いて描くため、この限りではありません。磁場の強さの単位には \(\text{G}\) (ガウス) が使われることもあり、\(1 \ \text{G}=10^{-4} \ \text{T}\) です。
 ) 程度です。これは黒点に比べるとやや弱いですが、太陽表面や大気で観測される磁場の中ではそれに次いで強い磁場です。
) 程度です。これは黒点に比べるとやや弱いですが、太陽表面や大気で観測される磁場の中ではそれに次いで強い磁場です。
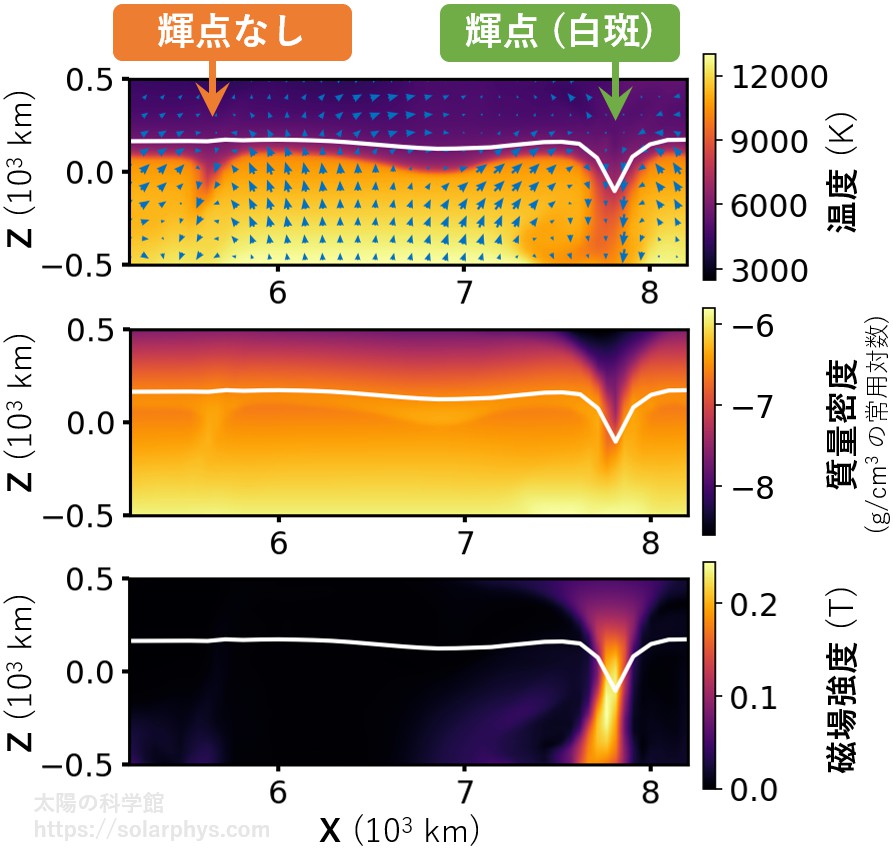
なぜ明るいのか?
図を見ると、輝点 (白斑) のある領域の質量密度は周りより一桁程低い ( = 希薄である) ことが分かります。先ほど温度が低いと気体は透明になると述べましたが、気体は薄くなっても透明になります。図には表面として見える高度が白線で示されていますが、輝点の形成域には文字通り「穴」が開いていることが分かります。図 4 ( 図 15 ) の白斑は粒状斑の間の領域が谷になっているように見えると上で述べましたが、その直感は正しいわけです。穴の深さは数百 km です。
太陽内部は基本的に深くなる程高温になっています。表面で冷やされた比較的低温の気体を見ているために、粒状斑の間の領域は暗く見えていると述べました。しかし、穴が開いている場合、より深い層の高温の気体が穴の壁面として見えるため、斜めからこの穴を見た場合は周囲より明るい白斑として写ります。
なぜ穴が開いているのか?
輝点 (白斑) の形成域に穴が開いている現象をウィルソン効果 (Wilson depression) と言います。ウィルソン効果は輝点だけでなく、黒点でも見られます。記事「黒点:磁場が通り抜ける「穴」」で説明していますが、黒点もやはり \(0.1 \ \text{T}\) の桁数の磁場が存在する領域です。このように、強い磁場が存在する領域の表面は凹んで見える (気体が希薄になる) という普遍的な傾向があります。
詳しくは記事「プラズマと磁場:磁力線が「実体」を帯びる」で説明しますが、太陽表面を構成するプラズマ ( = 電気を通しやすい気体) と磁場は一心同体です。太陽表面に磁場が存在すると、その付近には普通電流も存在します。磁場と電流の関係はアンペールの法則に従わなければなりません。磁場の存在下で電流が気体を流れると、気体は
ローレンツ力
脚注
[ローレンツ力]:電荷を持った粒子が磁場の中を運動をすると図の向きにローレンツ力を受けます。太陽を構成するプラズマ ( = 電気を通しやすい気体) は荷電粒子の集団であるため、電流 ( = 陽イオンと電子の間の相対的な動き) が発生すると各粒子にはたらくローレンツ力の合計としての力を受けることになります。単位体積あたりにはたらくローレンツ力 (単位 \(\text{N/m}^3\)) は電流 (単位 \(\text{A/m}^2\)) と磁場 (単位 \(\text{T}\)) の外積になります。
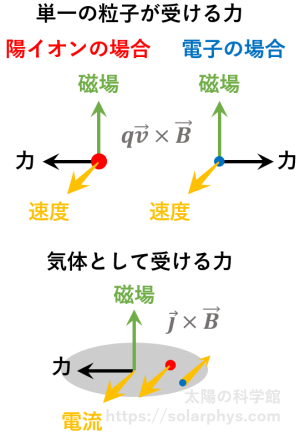 を受けます。この磁場と気体の相互作用を逐一追うと複雑ですが、整理すると次のように直観的に理解することができます。
を受けます。この磁場と気体の相互作用を逐一追うと複雑ですが、整理すると次のように直観的に理解することができます。
磁場が存在すると、プラズマ (気体) は
磁力線
脚注
[磁力線]:各場所での磁場の向きを繋げた曲線を磁力線と言います。理想的には磁力線の密集度がその場所での磁場の強さ (単位 T, テスラ) を表しますが、実際の図では特徴的な磁力線だけを間引いて描くため、この限りではありません。磁力線が分裂したり合流したりすることはありません。電気を通すプラズマでは磁力線は物質に凍結している (物質は磁力線に垂直な方向に動くことができない) ので、磁力線の動きはその場所でのプラズマ (物質) の動きを表します。
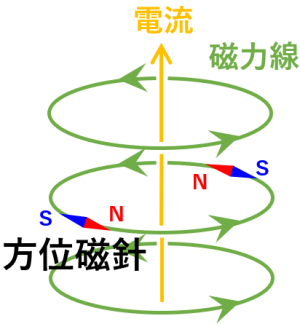 が互いに離れようとする向きにローレンツ力を受けます。この力は気体の圧力と同じような性質を持っており、磁気圧 (magnetic pressure) と呼ばれます。その大きさ \(P_\text{磁気}\) [\(\text{Pa}\)] は磁場強度 \(B\) [\(\text{T}\)] の 2 乗に比例し、次のように書けます。
が互いに離れようとする向きにローレンツ力を受けます。この力は気体の圧力と同じような性質を持っており、磁気圧 (magnetic pressure) と呼ばれます。その大きさ \(P_\text{磁気}\) [\(\text{Pa}\)] は磁場強度 \(B\) [\(\text{T}\)] の 2 乗に比例し、次のように書けます。
\begin{align} P_\text{磁気} &= \frac{B^2}{2\mu_0} \tag{1} \\ \text{ただし}, \quad \mu_0 &= 1.26\times 10^{-6} \ \text{T}^2\text{Pa}^{-1} \\ &: \text{真空の透磁率}\end{align}
地球の大気は太陽と同じように 重力成層 脚注 [重力成層]:下向きに重力がかかっているところに気体が積み重なると、下の気体は上に乗っている気体に押しつぶされて密度や圧力が高くなります。このように、上に行くほど密度や圧力が低くなるように気体が積み重なった状態を重力成層と言います。地球の大気も重力成層しているため、高い山に登ると空気が薄くなります。 しています。一定の高度に注目すると、その高度での大気圧は基本的にどこでも同程度の大きさになっています。例えば 図 19 に示した日のように、紀伊半島沖は台風が来ていて \(950 \ \text{hPa}\) であるのに対し、北海道は高気圧に守られていて \(1020 \ \text{hPa}\) であるというような差が生まれることはありますが、いずれにせよ海面高度での気圧は \(1000 \ \text{hPa} \approx 1\) 気圧の桁数です。
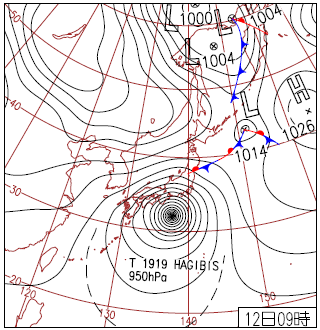
このことは太陽表面付近の高度の場合にも大雑把には成り立っていると考えられています。ただし、太陽の場合は磁気圧も考慮する必要があります。図 20 に示したように、気体の圧力と磁気圧の合計値が同じ高度ではおよその桁数として一致します。
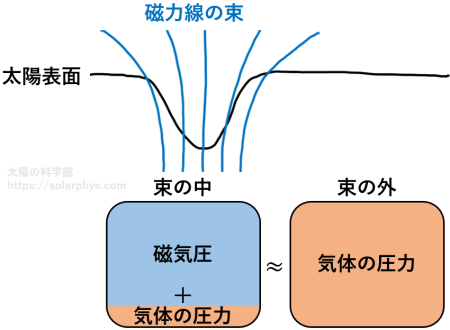
太陽表面の磁場のない領域での気体の圧力 (ガス圧, gas pressure) は \(9000 \ \text{Pa}\) 程度の桁数です。一方で、白斑に存在する典型的な磁場の強さ \(0.15 \ \text{T}\) を 式 (1) に代入すると、強磁場領域内部での磁気圧は \(9000 \ \text{Pa}\) 程度だと分かります。つまり、強磁場内部の磁気圧はそれ自身で外部のガス圧と釣り合ってしまう程の大きさを持ちます。
このため、内部のガス圧が外部と同程度の大きさを持つことはできません。理想気体の状態方程式によると、気体の圧力は密度に比例します。従って、強磁場の存在域の密度は桁違いに小さくならざるを得ません。このような力のバランスによって、強磁場の存在域には穴が開いています。
黒点は暗いのに輝点が明るいのはなぜか?
黒点と輝点はどちらも太陽表面において強い磁場が存在する領域であると述べました。しかし、前者は暗く (低温に)、後者は明るく (高温に) 写ります。この差は一言でいうと、強磁場の存在する面積の違いに起因します。輝点は粒状斑と粒状斑の間にできる構造であるのに対し、黒点は小さいもので粒状斑の数個分、大きいものだと百個分近くの大きさに渡って強い磁場が存在する現象です ( 図 21 )。
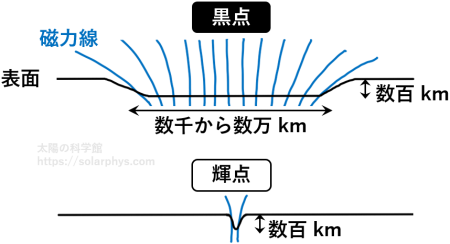
黒点の記事 で説明しているように、強い磁場が存在すると熱対流が抑制されるため、内部から表面に運ばれてくる熱量が減ります。黒点はこの影響で温度が大きく下がり、深い層の気体を見ているのにもかかわらず周囲の粒状斑より暗く写ります。
輝点の場合もやはり、磁力線の束の内部の対流は抑えられていますが、こちらの場合は穴が狭いため、穴の壁面が内部を照らすことによって内部が温められており、周囲より大きく温度が下がることはありません。このため、粒状斑と同程度の明るさに写ります。
参考文献
記事全体として参考にしたレビュー
- Borrero, J. M., Jafarzadeh, S., Schüssler, M. and Solanki, S. K. (2017). Solar magnetoconvection and small-scale dynamo. Space Science Reviews, 210, 275-316 .
- Nordlund, Å., Stein, R. F. and Asplund, M. (2009). Solar surface convection. Living Reviews in Solar Physics, 6, 2 .
- Rincon, F. and Rieutord, M. (2018). The Sun’s supergranulation. Living Reviews in Solar Physics, 15, 6 .
引用した文献
- Carlsson, M., Hansteen, V. H., Gudiksen, B. V., Leenaarts, J. and De Pontieu, B. (2016). A publicly available simulation of an enhanced network region of the Sun. Astronomy & Astrophysics, 585, A4 .
- Gudiksen, B. V., Carlsson, M., Hansteen, V. H., Hayek, W., Leenaarts, J. and Martínez-Sykora, J. (2011). The stellar atmosphere simulation code Bifrost. Astronomy & Astrophysics, 531, A154 .
- Kianfar, S., Leenaarts, J., Danilovic, S., de la Cruz Rodríguez, J. and José Díaz Baso, C. (2020). Physical properties of bright Ca II K fibrils in the solar chromosphere. Astronomy & Astrophysics, 637, A1 .
- Langfellner, J., Birch, A. C. and Gizon, L. (2016). Intensity contrast of the average supergranule. Astronomy & Astrophysics, 596, A66 .