ゼーマン効果

まえがき

この記事は別の記事「プラズマ診断：太陽を「見る」だけでここまで分かる」の補足という形で載せています。太陽表面に強い磁場が存在した場合に、観測される光のスペクトルや偏光状態が変化する現象の文脈での説明になります。

この記事はややマニア度の高い記事です。前提知識として、光の基本知識について記事「光とは何か？」、偏光とは何かについて記事「偏光とは何か？：光の持つ 2 つの状態」を読んでいただければ、理解しやすくなると思います。

どのような現象か

観測例

図 1 に示したのは、JAXA/ISAS が主体となって開発した観測衛星ひのでに搭載された装置 SP が観測した太陽光のスペクトルです。スペクトルとは、各波長ごとの光の強度 (明るさ) を描いたグラフです。図に示されている波長 630 nm とは、色でいうと赤に相当します。

図の A (青色) のグラフは、太陽面のうち、磁場の弱い領域を観測した場合の結果です。対して、B (赤色) のグラフは、黒点内の磁場の強い領域を観測した結果です。より詳しくは プラズマ診断の記事 で説明しています。

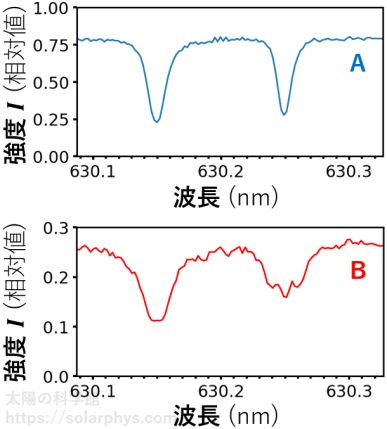
図には 2 つの 吸収線 脚注 [吸収線]：太陽からの光をスペクトル分解 ( = 各波長ごとの強度を表示) すると、周りと比べて強度の弱い波長帯が所々に現れます。これを吸収線と言います。逆に、どの吸収線にも該当しないような波長の光を連続光と言います。 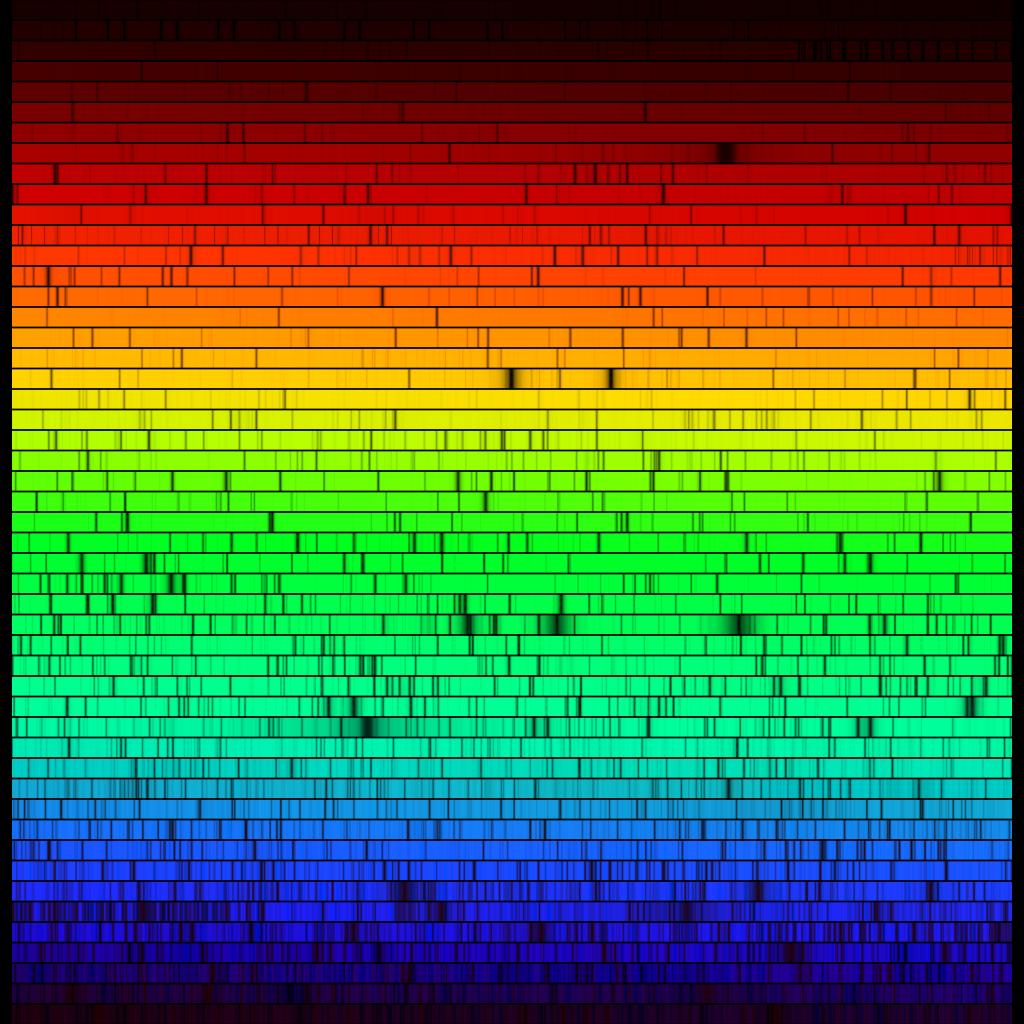図：太陽光を各波長 (色) ごとに分解したもの。黒く見える波長が吸収線。提供 N.A.Sharp, NOAO/NSO/Kitt Peak FTS/AURA/NSF が写っています。吸収線とは、スペクトルが鋭く凹んだ部分のことです。磁場の強い領域で形成された吸収線 (赤色) は、磁場の弱い領域 (青色) の場合より太くなっていることが確認できます。また、B のグラフの右側の吸収線は、先が 3 つに分裂しているように見える気がします。

図 2 は 図 1 と同じ領域を観測して得られたストークスパラメータです。グラフの色は 図 1 と揃えてあります。詳しくは 偏光の記事 で説明していますが、ストークスパラメータとは、観測された光の偏光状態を記述する量です。強度 \(I\) に加えて、\(Q, U, V\) という 3 つの量を観測することで、偏光状態を一意に決定することができます。

図を見ると、磁場の弱い領域を観測した場合 (青色) は、\(Q, U, V\) の値はゼロに近いことが確認できます。このような偏光状態を「無偏光」と言います。

対して、磁場の強い領域の場合 (赤色) は、これらの絶対値が吸収線に相当する波長で大きくなっています。観測光に直線偏光した光子が多く含まれる場合、言い換えると、観測光が部分的に直線偏光している場合は、\(Q, U\) の絶対値が大きくなります。円偏光の光子が多く含まれる場合は、\(V\) の絶対値が大きくなります。

観測事実

上で示したような現象は、ゼーマン効果と呼ばれます。ゼーマン効果は磁場の強い領域で吸収されることによって形成された吸収線を観測した場合に見られます。

磁場の強さや視線方向に対する向きによって、観測される吸収線やストークスパラメータの値は変わります。どのように変化するのかを模式的に示した動画を 図 3 に示します。図の左は視線方向に対する磁場ベクトルの様子を表し、右はそのような磁場が存在した際に観測されるストークスパラメータの様子を表します。

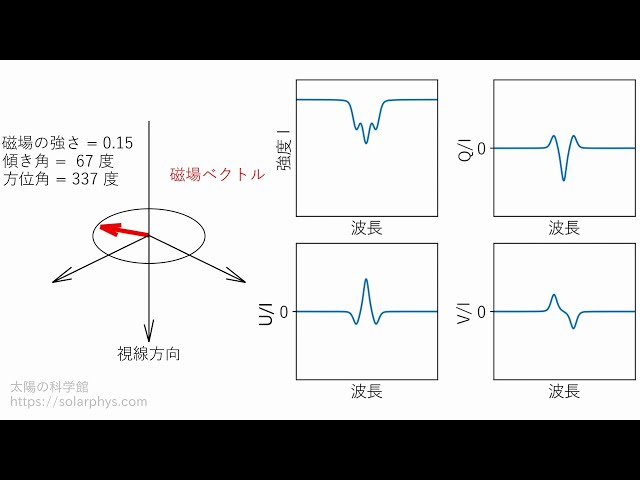
ゼーマン効果の観測的特徴をまとめると、次の 2 つです。

• 磁場が弱い場合には 1 つだった吸収線が、複数に分裂する。あるいは、磁場の強さが不十分な場合は、完全に分裂しきらずに重なることで、吸収線が太くなったように見える。分裂の本数は磁場の向きによって変わる。
• 分裂した各吸収線に相当する波長は、ストークスパラメータの値がゼロではなくなっている。

このような観測事実は次のような機構が働いていると考えれば説明できます。観測される光は光子と呼ばれる最小単位の集団と解釈できます。それぞれの光子が波長という性質を持っていると考えてください。

図 1 に写っている吸収線は、太陽表面で発せられた光子の一部が、少し上の 光球 脚注 [光球]：フィルターを通さずに可視光で観測したときに明るく映る層のことです。大雑把にはこの層が「太陽表面」と呼ばれます。より細かくは高度 0 から 500 km あたりの層を言います。 と呼ばれる層に存在する鉄原子によって吸収されることで形成されています ( 図 4 )。鉄原子は全ての波長の光子を吸収できるわけではなく、例えば 630.15 nm や 630.25 nm の光子を吸収しやすい性質を持ちます。故に、その波長の光子だけが取り除かれることで、図 1 のように凹んだ形のスペクトルが観測されます。吸収線の形成についてのより詳しい説明は、記事「スペクトル線：なぜ様々な光で観測するのか？」を読んでください。

観測される光の偏光状態とは、含まれる個々の光子の偏光についての統計的性質です。各光子が完全にランダムな偏光にあるときの光の状態を無偏光と言います。例えば直線偏光の光子が多く含まれる場合、その光は全体として直線偏光していると表現され、観測される \(Q, U\) の値が非ゼロになります。

太陽表面が発する光は無偏光です。磁場が無い場合、図 5 の左に示したように、波長 630.25 nm には 1 つの吸収線が存在します。これは、偏光状態に関わらず満遍なく光子が吸収されることで形成されたものです。よって、観測される光も無偏光のままであり、\(Q, U, V\) はゼロに近い値を取ります。

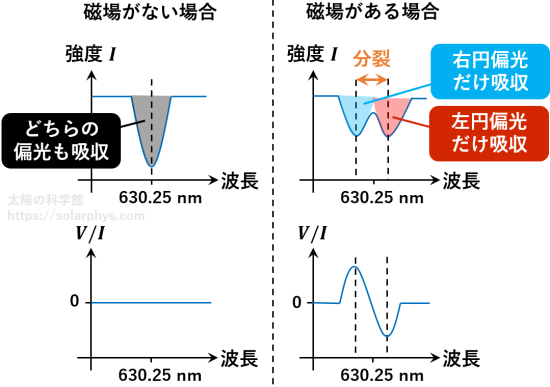
対して、光球に強い磁場が存在する場合、図の右のように、吸収線が複数に分裂します。そして、それぞれは特定の偏光状態の光子のみを吸収することで形成されます。例えば図のように 2 個に分裂した場合、片方の波長では左円偏光、もう一方は右円偏光の光子のみが吸収されています。

詳しくは 偏光の記事 で説明していますが、例えば無偏光の光 ( = 光子の集団) から、左円偏光の光子のみが吸収されて取り除かれた場合、残った光は右円偏光に偏ります。このような過程を踏むことで、分裂した各吸収線の波長では、ゼロではない値のストークスパラメータが観測されます。

この記事では、強い磁場が存在すると吸収線が分裂する仕組み、各々の吸収線が特定の偏光状態の光子のみを吸収する理由について説明します。

束縛電子の運動

既に述べたように、吸収線は原子が光子を吸収することで形成されます。ゼーマン効果を説明するには、まず原子の構造について説明する必要があります。

例えば上の説明で登場した鉄原子は、1 個の原子核と 26 個の電子から成ります。鉄の原子核は +26 の電荷を持ち、-1 の電荷を持つ電子が 26 個、いわゆる「クーロン力」によって原子核に引き寄せられて、周りを運動しています。これを電子が原子内に束縛されていると表現します。

原子のようなミクロな世界での「運動」は、高校物理で習うようないわゆる「ニュートン力学」ではなく、「量子力学」という大学で初めて習う理論を用いることで正しく考えられます。そのため、束縛された電子の運動を、惑星が太陽の周りを回る運動のようなものと想像していると、ときに勘違いが発生します。しかし、量子力学も「力学」という名がついている以上、エネルギーや運動量のような概念は基本的に共通します。

量子力学を踏まえ、電子の運動を簡単に考えられるようにまとめられたものが、高校化学で習う電子配置 (電子軌道) です。この考え方では、原子が電子の入り得る軌道を持ちます。それぞれの軌道の相対的なエネルギーの高さはある程度決まっていて、基本的にはエネルギーの低い軌道から、2 個の電子によって埋められていきます ( 図 6 )。

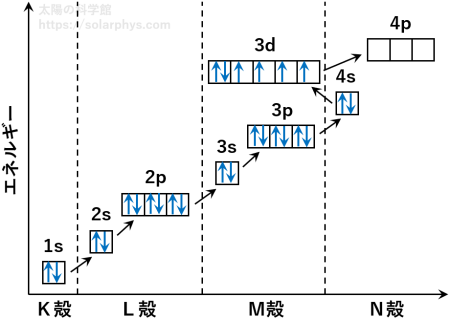
鉄原子の場合は 図 6 のように、エネルギーの低い方から 26 本の矢印を埋めていくと、3d 軌道の一部まで占有されます。この状態が、束縛電子全体のエネルギーがいちばん低い状態です。基底状態と言います。

電子は 図 6 のように敷き詰められなければならないわけではなく、例えば 図 7 のように、4s 軌道の電子の内の 1 個が 4p 軌道を占有することも可能です。これを励起状態と言います。この場合、基底状態より電子全体のエネルギーが高くなります。

基本的に、エネルギーの低い状態の方がより安定して存在するため、光球の気体を考えたとき、そこに含まれる鉄原子のほとんどは基底状態にあります。しかし、励起状態の原子も、基底状態に比べれば少ないですが、ある程度存在します。

束縛-束縛遷移

原子に束縛された電子の量子力学的な運動は、電子軌道を考えることで整理できると述べました。鉄原子の場合、26 個の電子が軌道を占有する仕方は何通りもあり、それぞれの電子配置によって、電子全体での力学的エネルギーの合計は異なる値になります。

光球 脚注 [光球]：フィルターを通さずに可視光で観測したときに明るく映る層のことです。大雑把にはこの層が「太陽表面」と呼ばれます。より細かくは高度 0 から 500 km あたりの層を言います。 では、原子が光子を吸収し、より高いエネルギーの電子配置に変化する反応が頻繁に起きます。この反応によって、吸収線が形成されます。

例えば 図 1 の右側 (波長 630.25 nm) の吸収線に注目します。この吸収線は、図 8 下段に示した電子配置にあった鉄原子が、上段の配置に変化する反応によって形成されます。仮に、下段の配置を a、上段を b と名付けます。

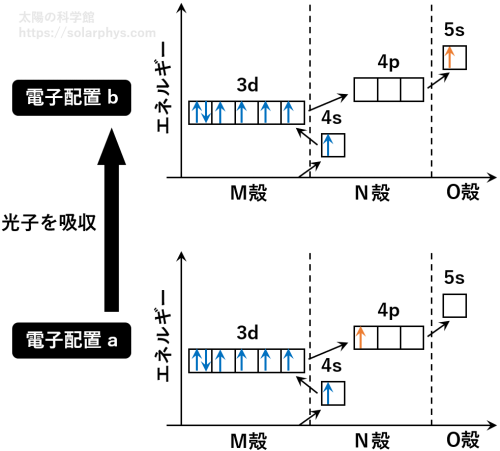
細かい話をすると、配置 a でも具体的に 5 個ある 3d 軌道や 3 個ある 4p 軌道のうちのどれが占有されているかなどによって、電子全体のエネルギー値は少しずつ変わってきます。630.25 nm の吸収線は、 図 9 に示したエネルギー値を持つ配置 a, b 間の反応に対応します ( Nave et al., 1994 )。

配置 a と b のエネルギー差は \(3.1510\times 10^{-19} \ \text{J}\) です。反応の前後では、エネルギーの総量は保存しなければなりません。つまり、この反応によって、ちょうど \(3.1510\times 10^{-19} \ \text{J}\) のエネルギーを持つ光子が吸収されなければなりません。

光の記事 でも説明していますが、光子のエネルギーとは、波長の逆数に相当する性質です。具体的には、光子のエネルギー \(E\) [\(\text{J}\)] と波長 \(\lambda\) [\(\text{m}\)] の間には次の関係が成り立ちます。

\begin{align} E &= \frac{hc}{\lambda} \\ \text{ただし},\quad h &= 6.62607 \times 10^{-34} \ \text{J s} \\ &: \text{プランク定数} \\ c &= 2.99792 \times 10^8 \ \text{m/s} \\ &: \text{光速}\end{align}

上式の関係を用いてエネルギーを波長に換算すると、この反応では波長 630.42 nm の光子のみが吸収されることが分かります。

今は 630.25 nm の吸収線を考えていたのに、これではおかしいのではないかと思われるかもしれません。これにはもうひとつ、歴史的な慣習によるカラクリが存在します。

光は真空中と空気中では、その伝搬速度が異なります。上式で「光速」として示したのは真空中での伝搬速度です。空気中では少し遅くなります。

図 1 などで横軸に示されている波長は、暗黙の了解として、光子が空気中を伝搬していると仮定した場合の波長を指します。上で算出した波長は真空中での波長なので、図 1 と比較するには、これを空気中での波長に換算する必要があります。

エドレンの式 ( Edlén, 1966 ) を用いると、波長 630 nm 付近の光子に対する空気の屈折率は 1.00027 と計算されます。630.42 nm をこれで割ると、630.25 nm になります。

磁場が存在すると...

磁場の中に原子が置かれたときの挙動を説明するには、電子が持つ「角運動量」について説明する必要があります。

角運動量とは

高校では、エネルギーと運動量の 2 種類の保存量を習いますが、運動を考える上でもう一つ重要な保存量があります。それは角運動量です。物体が直線運動をすると運動量を持ちますが、回転運動をすると角運動量を持ちます。

角運動量はベクトル量です。その向きは回転軸の向きを表し、大きさは簡単に言うと回転の「勢い」を表します。例えば、図 10 のように回転しているコマは、図の矢印の向きに角運動量を持ちます。コマが速く回転すると角運動量は大きくなりますし、同じ回転速度でも、重いコマや大きなコマほど角運動量は大きいです。

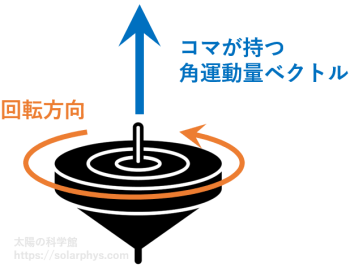
回転するコマは、特に手で押したりしない限り、倒れずに回転を続けます。これは角運動量が保存するためです。外界から力を受けない限り、角運動量の向きと大きさは変化しません。

ただし、長期的に見ると、コマの場合は地面との間に摩擦力が働くため、回転の速度は落ち、角運動量の大きさは小さくなっていきます。十分に小さくなると、重力によるトルクが無視できなくなり、角運動量の向きが変えられ、倒れます。

束縛電子の場合

しばしば電子は原子核の周りを「回っている」と表現されますが、これは束縛された電子が角運動量を持っていることを言っています。角運動量の大きさや向きは、その電子が占めている軌道によって異なります。これを軌道角運動量と言います。具体的には、例えば 3s, 3p, 3d 軌道間では軌道角運動量の大きさが異なり、5 個ある 3d 軌道はそれぞれ向きが違うという具合です。

また、電子は軌道角運動量とは別に、スピン角運動量と呼ばれる角運動量も持ちます。これは時々電子が「自転」していると表現されますが、もちろん量子力学を用いることで初めて考えることができる運動です。

電子のような電荷を持った粒子が回転運動をすると、粒子間に複雑な相互作用が起こります。鉄原子は 26 個の電子を持ちますが、これらの電子が持つ軌道角運動量とスピン角運動量の間の関係によって、電子全体のエネルギー値は少しずつ変化します。言い換えると、すでに述べたように、同じ電子配置 a でも、具体的な占有軌道によってエネルギーは違います。

26 個の電子が持つ軌道角運動量とスピン角運動量全てをベクトル的に合成した角運動量を考えます。波長 630.25 nm の吸収線は、この全角運動量の大きさが \(\hbar\) であるような電子配置 a と、全角運動量の大きさがゼロであるような電子配置 b の間で起きる反応に対応します。\(\hbar = 1.05 \times 10^{-34} \ \text{J s}\) は、ディラック定数と呼ばれる、角運動量の次元を持つ物理定数です。

角運動量の向き

さて、量子力学は不思議な理論であり、大抵の物理量は飛び飛びの値しかとり得ません。例えば、電子のエネルギーが飛び飛びの値しかとり得ないという事実が、上で説明した、エネルギー値の決まった軌道を考え、それを電子で埋めていくという考え方に組み込まれています。例えば 4s 軌道と 3d 軌道の間のエネルギー値は取ることができないわけです。

角運動量の向きも飛び飛びの値しかとり得ません。今注目している電子配置 a は全角運動量の大きさが \(\hbar\) であると述べましたが、その向きは原子によって違います。この場合、適当な方向に \(z\) 軸を取ると、全角運動量の向きは次の 3 つの状態しかとり得ません。

• \(z\) 軸正の向き
• \(z\) 軸に垂直な向き
• \(z\) 軸負の向き

\(z\) 軸は好きな方向にとれますが、一旦決めてしまえば、上の 3 つの状態しか考えることができません。\(z\) 軸に対して 45 度傾いた状態なんてものは御法度です。

つまり、上の説明では大雑把に電子配置 a と b の間の反応と述べましたが、より具体的には、今注目している電子配置 a は更に 表 11 の 3 つに分類できます。それぞれの配置を a+, a0, a- と呼ぶことにします。対して、電子配置 b の全角運動量の大きさはゼロなので、角運動量の向きを考えることはできず、これ以上分類できません。

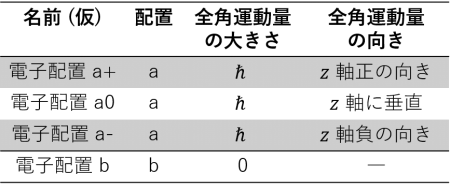
光球には a+, a0, a- それぞれの配置を持つ鉄原子が存在します。光球の磁場が弱い場合、光子を吸収して、これらの配置から配置 b に変化する 3 種類の反応によって、630.25 nm の吸収線は形成されています ( 図 12 )。

磁場が強いと分裂する

電荷を持った粒子の運動と磁場は、互いに影響を及ぼし合います。例えば、磁場が存在すると電流は ローレンツ力 脚注 [ローレンツ力]：電荷を持った粒子が磁場の中を運動をすると図の向きにローレンツ力を受けます。太陽を構成するプラズマ ( = 電気を通しやすい気体) は荷電粒子の集団であるため、電流 ( = 陽イオンと電子の間の相対的な動き) が発生すると各粒子にはたらくローレンツ力の合計としての力を受けることになります。単位体積あたりにはたらくローレンツ力 (単位 \(\text{N/m}^3\)) は電流 (単位 \(\text{A/m}^2\)) と磁場 (単位 \(\text{T}\)) の外積になります。 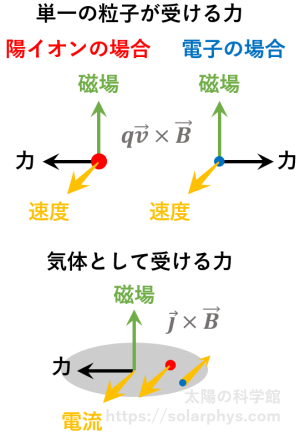を受けることを高校物理で習います。電流とは、金属中の自由電子の流れです。

原子に束縛された電子の運動も例外ではありません。鉄原子が強い磁場の中に存在している場合、束縛電子の力学的エネルギーは変化します。そして、その変化の仕方は全角運動量によって違います。

電子の電荷は負なので、磁場と同じ向きに角運動量を持つような運動をしている場合にはエネルギーがより高くなり、逆向きの場合は低くなります。角運動量が磁場と垂直な場合は、磁場の存在によってエネルギー値は影響を受けません。

磁場の向きに \(z\) 軸を取って考えます。このとき、配置 a0 は磁場と垂直な向きに全角運動量を持つ状態なので、エネルギー値の変化はありません。一方で、配置 a+ のエネルギー値は高くなり、 a- は低くなります ( 図 13 )。これをゼーマン分裂と言います。分裂の幅は基本的に磁場の強さに比例します。

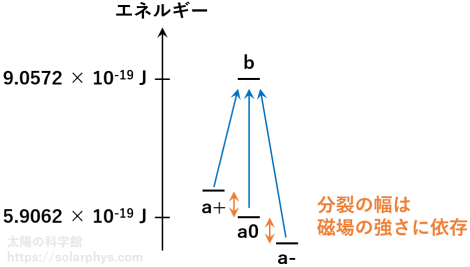
配置 a+, a0, a- と b の間のエネルギー差がそれぞれ違う値になるため、それぞれの反応で吸収される光子の波長も変化します。具体的には、 a+ と b 間の反応では、630.25 nm より少し長い波長の光子が吸収されるようになります。対して、a- と b 間の反応では、より波長の短い光子が吸収されます。 a0 と b 間の反応は、磁場のない場合と同じ 630.25 nm の光子を吸収します。

こうして、強い磁場がある場合には、630.25 nm の吸収線は最大で 3 つに分裂することになります。ただし、次の節で述べるように、磁場が観測機の視線方向と (反) 平行である場合には、a0 - b 間の反応に伴う光子の吸収が起きないため、真ん中の吸収線は見えません。つまり、吸収線は 2 つに分裂しているように見えます。

なぜ偏光するのか

前節までで、吸収線が形成される領域に強い磁場が存在する場合に、吸収線が複数に分裂する仕組みについて説明しました。本質的に吸収線が 3 つに分裂しても、実際に観測される数は 2 つである場合もあると述べました。

本節ではその理由と、分裂した各吸収線が特定の偏光状態の光子しか吸収しない理由について説明します。これらは角運動量の保存則によって説明できます。

光子の持つ角運動量

上の方で、電子はスピン角運動量と呼ばれる角運動量を持つと述べましたが、光子もスピン角運動量を持ちます。そして、それは偏光状態に関係します。

光子のスピン角運動量の大きさは \(\hbar\) と決まっています。\(\hbar\) は先ほども出てきたディラック定数です。

スピン角運動量の向きは、光子の伝搬方向か、それとは逆の向きかの 2 通りしかとり得ません。右円偏光の光子は伝搬方向と同じ向きのスピン角運動量を持ちます。対して、左円偏光の光子は逆向きです ( 図 14 )。

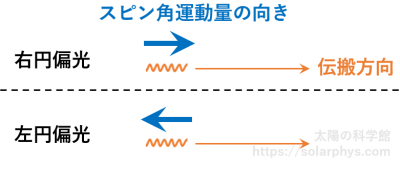
残念ながら、どちらの向きのスピン角運動量を持つ光子を右/左と呼ぶかの流儀は双方存在します。本サイトの説明では、基本的に Landi Degl'Innocenti & Landolfi (2004) の定義方法に従っていますが、逆の定義が用いられている場合もあります。例えば、日本天文学会が運営する 天文学辞典 の「円偏光」の項で説明されている「左円偏光」は、本サイトの右円偏光のことです。

では、直線偏光の光子はどの向きにスピン角運動量を持つのか疑問を持たれると思います。偏光の記事 で説明しているように、直線偏光は右円偏光と左円偏光を波的に (数学的に) 重ね合わせた状態と解釈できます。いわば「スピン角運動量の向きは伝搬方向かもしれないし、逆向きかもしれない」状態です。そのような状態を考えることができてしまうのが量子力学の特徴です。

磁場が視線方向と平行な場合

光球の磁場が、観測機の視線方向と反平行であった場合に、分裂した吸収線がどのように偏光するのかを考えます。他の向きの場合について一般的に考察するには、量子力学の数式が必要になりますが、(反) 平行の場合ならば、今までに説明した知識で十分です。この場合、磁場と同じ向きに伝搬する光子を鉄原子がどのように吸収するかについて考察することになります ( 図 15 )。

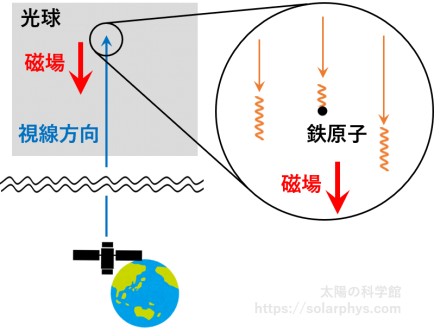
前の節での結果をまとめると、この記事で注目している吸収線に関係する反応の磁場中での性質は 表 16 のようになります。

光子の吸収反応では、角運動量が保存されなければなりません。つまり、関係する粒子の持つ角運動量をベクトル的に合成したものは、反応の前後で等しくなります。

図 17 のように考えることで、配置 a+ から b への反応では左円偏光、a- から b への反応では右円偏光の光子のみが吸収されることが分かります。

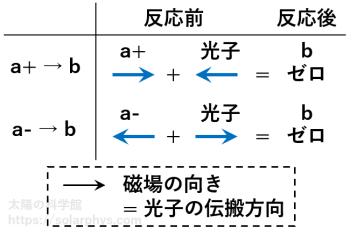
光子の角運動量のとり得る向きは伝搬方向と同じか、逆向きかの 2 通りしかないので、a0 から b への反応については、どのような偏光状態の光子に対しても角運動量保存則を満たすことができません。よって、この反応が起きることはありません。

まとめると、磁場が視線方向と反平行であった場合、630.25 nm の吸収線は 2 つに分裂しているように見えます。波長の長い方の吸収線では、左円偏光の光子だけが吸収されることで観測光は右円偏光になっており、波長の短い方では逆に左円偏光になっています。

図 2 の観測例や 図 3 の動画のストークス \(V\) は、観測光が左円偏光にある場合に正の値を持ち、右円偏光にある場合に負の値を持つような定義になっています。

参考文献

記事全体として参考にした書籍

• Landi Degl'Innocenti, E. and Landolfi, M. (2004). Polarization in Spectral Lines (Dordrecht: Springer ).

引用した文献

• Edlén, B. (1966). The refractive index of air. Metrologia, 2, 71-80 .
• Lites, B. W. and Ichimoto, K. (2013). The SP_PREP data preparation package for the Hinode Spectro-Polarimeter. Solar Physics, 283, 601-629 .
• Nave, G., Johansson, S., Learner, R. C. M., Thorne, A. P. and Brault, J. W. (1994). A new multiplet table for Fe I. The Astrophysical Journal Supplement Series, 94, 221-459 .