太陽の観測
太陽で起きている現象を知るために観測が行われます。太陽を観測する手法は大きく次の 4 つに分けられます ( 図 1 )。
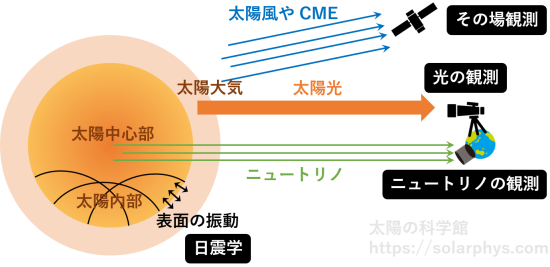
- 光の観測：太陽表面や大気から放たれる光を地上の望遠鏡または観測衛星を用いて観測することで、光が放たれた場所の情報を得ます。
- その場観測：観測衛星を用いて太陽が放つ太陽風や CME のような物質粒子や磁場を直接捉え、その性質を分析します。
- 日震学：太陽表面で放たれる光の観測から、表面で起きている振動の様子を知ることができます。その情報から太陽内部での波の伝わり方を推定することで、内部の情報を得ることができます。
- ニュートリノ観測：太陽中心部で核融合に伴って放出されるニュートリノを地上で捉えることで、核融合の様式や中心部の状態についての情報を得ます。
地球に届く太陽光を分析することで、光が放たれた場所の情報を得ることができます。具体的には、記事「スペクトル線：なぜ様々な光で観測するのか？」で説明している吸収線や輝線を観測し、その波長や偏光状態を調べることで、太陽表面や大気の気体の動きや温度、磁場の様子など、様々な情報が得られます。詳しくは記事「プラズマ診断：太陽を「見る」だけでここまで分かる」で説明しています。
太陽大気から放たれる物質の一部は、地球を直撃し、時に通信や人工衛星などに影響を与えます。太陽風や CME (コロナ質量放出) と呼ばれる現象です。観測衛星を用いて、これらの物質や物質と一緒に運ばれてくる磁場を宇宙空間で直接捉えることによって、その性質を調べる観測手法を「その場観測 (in-situ observation)」と言います。これらの現象については、記事「太陽風：常に噴き出すスプリンクラー」「CME：噴出するプラズマの雲」で説明しています。
太陽内部は不透明なので、光の観測では直接内部の情報を得ることができません。内部を知るために発展したのが 日震学 脚注 [日震学]：太陽表面で観測される気体の振動や波を解析することで、太陽内部の圧力や密度、流れの様子などを知ることができます。この手法を日震学と言います。日震学はこれまで、太陽内部の理論モデル (標準太陽モデル) の観測的裏付けを与えた他、太陽内部の自転 (差動回転) の様子も明らかにしました。 と呼ばれる手法です。太陽表面では様々な振動が起きていることが (光の観測によって) 知られています。この振動は、太陽内部を 音波 脚注 [音波]：プラズマ中も普通の気体と同じように、物質の疎密波 (縦波) が伝わります。これを音波と言います。音波の伝わる速さ (音速) は温度の 1/2 乗に比例するので、注目する場所ごとに異なります。 のような波が伝わった結果、表面が揺らされて起きる現象です。振動の様子を分析することで、内部の音速を推定することができます。そこから内部の密度のような状態や、気体の流れの様子を推定することができます。日震学について詳しくは記事「太陽内部を探る日震学」で説明しています。
記事「ニュートリノ問題：エネルギー源は何？」で説明していますが、太陽中心部では核融合が起きています。この核融合によって生成されたニュートリノは、太陽をすり抜けて地球まで届きます。そのニュートリノを観測し、どれくらいのエネルギーを持っているのかを分析することで、中心部で具体的にどのような核融合反応がどれくらい起きているのかを推定することができます。近年のニュートリノ観測技術の向上に伴って、太陽中心部の状態を探る貴重な手法として期待されています。
太陽観測の基本は光の観測と言えるでしょう。観測結果を理解するには光について知っておく必要があります。この記事では、そもそも光とは何かについて、基本知識を説明します。
光は波である
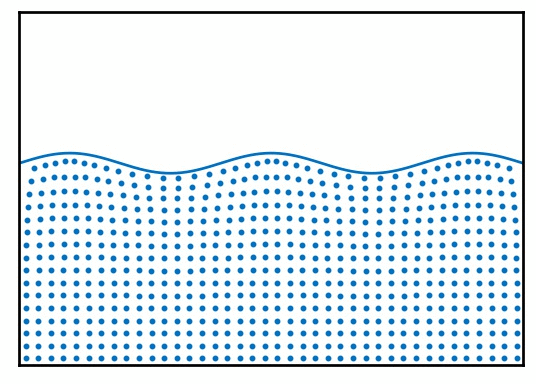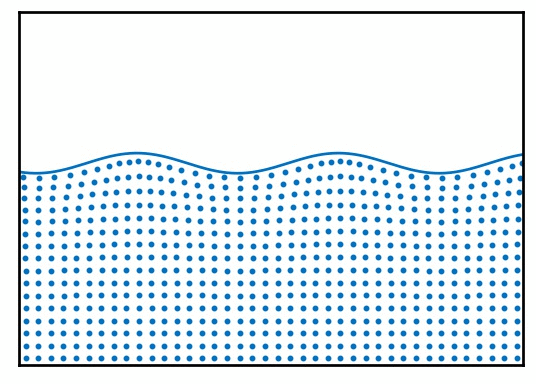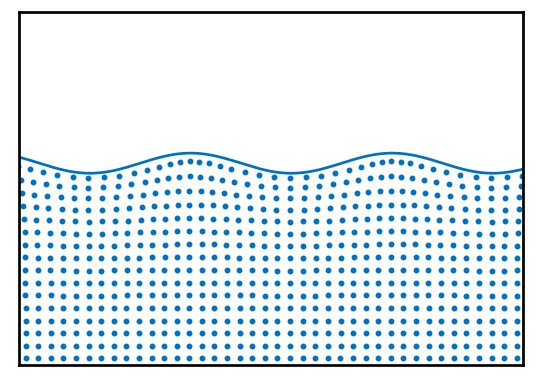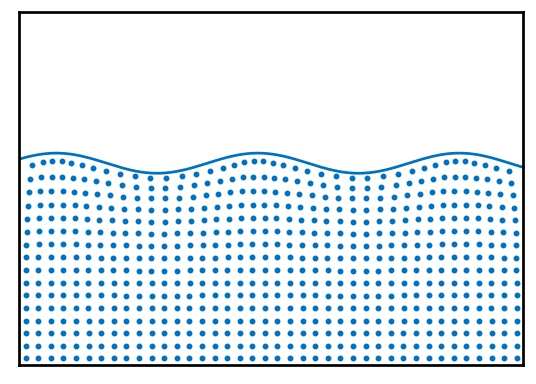
光は、その波の性質に注目したときの文脈では、電磁波とも呼ばれます。電磁波はその名の通り「波 (wave)」の性質を持ちます。身の回りで観察できる波には水面波があります。図 2 は水たまりに雨粒が落ちるのに伴って生成される水面波の様子です。
水たまりのそれぞれの位置での水 (物質) は、図 3 のように、その場で振動しているだけですが、その振動が隣の水を振動させ...という連鎖が起きることで、水面の形が移動するように見える現象が水面波です。
電磁波の場合に振動するのは、電場と磁場です。空間の各点において、電場・磁場というベクトル量を定義することができます。全くの真空の場合は、電場や磁場は全ての点においてゼロですが、例えば下敷きをセーターのような生地で擦ることで負に帯電させると、周りの電場は 図 4 のような値を持つようになります。
ここに髪の毛を近づけると、「誘電分極」という効果によって、髪の毛は正に帯電します。すると、髪の毛は (その場所の電場)\(\times\)(自分の持つ電荷量) だけの力を受け、下敷きに近づこうとします。これが身の回りで感じることのできる電場の例です。
磁場については記事「磁場とは？」で説明しています。電場と磁場は共に電磁場というものの一つの側面であり、切っても切り離せない関係です。
上で説明したのは、我々が目で見ることのできるスケールにおける電場ですが、もっとミクロな、原子や分子のスケールに注目してみます。例えば、白熱電球を点灯させるとします ( 図 5 )。
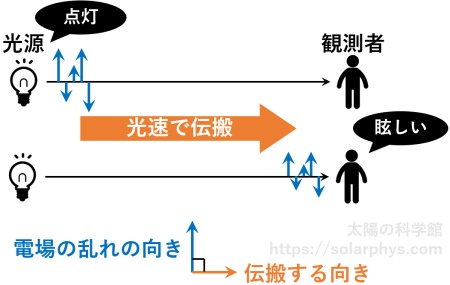
詳しくは記事「黒体放射：なぜ明るいのか？」で説明していますが、スイッチを入れて電球のフィラメントに電流が通ると、フィラメントを構成する原子達が周りの電場や磁場を乱し (震わせ) 始めます。すると、乱された電場や磁場が隣の点での電場と磁場を乱し... という連鎖が起き、電場と磁場の乱れが空間を伝わっていきます。これが電磁波です。
水面波は水面の 2 次元を伝わる波ですが、電磁波は空間を 3 次元的に伝わる波です。水面波の場合は、水の深さや波長によって伝搬速度が異なりますが、電磁波の伝搬速度は波長 ( = 色) に依らず一様に \(3\times 10^8 \ \text{m/s}\) (秒速 30 万 km) です。これを光速と言います。
電場と磁場の乱れが我々の目まで届くと、我々の目はその強さと色を検知します。このような過程を辿って、我々は「眩しい」「白色の光だ」などと認識するわけです。光の強さや色の意味については、下の節で説明します。
波は「縦波 (longitudinal wave)」と「横波 (transverse wave)」に分類することもできますが、電磁波は横波です。それに関連して、光は「偏光 (polarization)」と呼ばれる性質を持ちます。偏光については記事「偏光とは何か？：光の持つ 2 つの状態」で説明しています。
光は光子の集団である
電磁波や (振幅がそこまで大きくない) 水面波などの波は、「重ね合わせ」という考え方が通用します。例えば、図 6 の赤色の波形は、オレンジ色の 4 つの波形を足し合わせたものと解釈できます。
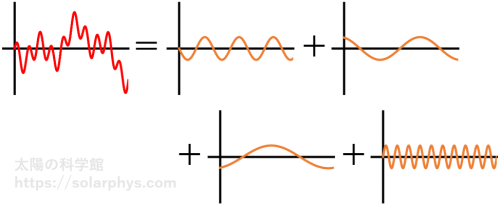
ただし、光の場合は、図のような波形の分解がどこまでもできるわけではなく、それ以上分解できない最小単位が存在します。これを「光子 (photon)」と言います。例えば望遠鏡で太陽の光を捉えているとき、望遠鏡の鏡筒に 1 秒あたりに飛び込んでくる光子の「個数」というものを考えることができます。
先ほどと同じように、白熱電球の場合を考えます。電球のフィラメントはたくさんの原子から成ります。それぞれの原子は様々なタイプの運動をしています。例えば金属内の自由電子は様々なエネルギー値を持ち得ますし、原子自体も隣の原子とばねで繋がれたような状態にあり、その場で振動しています。
「振動のエネルギーが小さくなる」「電子の持つエネルギーが小さくなる」といったように、何らかの運動の状態が変化すると、その変化で解放されたエネルギーが光子として放出されることがあります ( 図 7 )。個々の光子は短い光とイメージしてください。 1 回の変化で放出される光子は 1 個です。
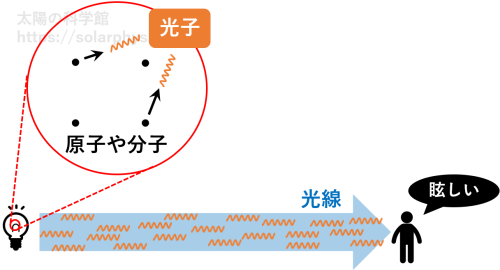
フィラメントはたくさんの原子から構成されるため、放出される光子の数もまた膨大です。各々の光子は光速で伝搬します。電球で発せられた光子の集団の一部は我々の目に届き、我々は眩しいと感じます。
光の波長とは何か
波長と色
光が波の性質を持つと言うからには、「波長 (wavelength)」という性質を考えることができます。光の波長とは、色に相当する概念です。個々の光子がそれぞれの波長を持っていると考えます。図 8 に、各波長域の光がどう呼ばれているかをまとめました。各名称の境界は厳密に決まっているわけではありません。
我々は大体波長 400 nm 付近から 800 nm 付近の狭い領域の光しか見ることができません。この領域を可視光 (visible light) と言います。可視光のうち、波長の短い側は青色、長い側は赤色に見えます。可視光より波長の短い側の目には見えない領域の光は、紫外線 (ultraviolet ray, UV ray)、 X 線 (X-ray)、ガンマ線 (gamma-ray)と呼ばれます。一方で、波長の長い側は赤外線 (infrared ray)、電波 (radio wave) と呼ばれます。携帯電話の通信に使われる電波の波長は 10 cm 程度です。
例えば、波長 470 nm は青色の可視光に相当します。我々が目にする光に含まれる光子のほとんどが 470 nm の波長を持っていた場合、この光は青色に見えます ( 図 9 の上 )。対して、目にする光が可視光の様々な波長の光子をバランスよく含んでいた場合、この光は白色に見えます ( 図 9 の下 )。
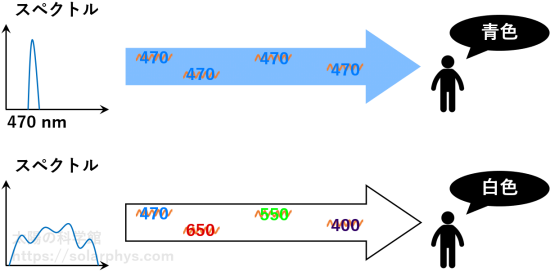
図の左に書いた「スペクトル (spectrum)」とは、横軸を波長、縦軸をその波長の光の強度としたグラフです。強度については後から説明しますが、含まれる光子の数に関係のある量です。スペクトルとは、含まれる光子がどのような波長を持っているのかの分布です。図の上の光は、 470 nm に集中した形のスペクトルを持つことになります。対して、下の白色の光は、広い波長域にまたがったスペクトルを持つでしょう。
波長と振動数
電磁波が波の性質を持つと言うからには、「振動数 (frequency)」という量も考えることができます。電磁波の場合、波長 \(\lambda \ [\text{m}]\) と振動数 \(\nu \ [\text{s}^{-1}]\) の間には次の関係があります。
\[\nu = \frac{c}{\lambda}\]
\(c\) は光速です。電磁波の場合、伝搬速度は波長に依らないため、波長が決まれば上式から振動数が決まり、逆に振動数が与えられれば上式から波長が分かります。つまり、波長と振動数は、光子の同じ性質を 2 通りの方法で表現したものと解釈できます。スペクトルのような図を見る際には、横軸が波長と振動数のどちらを表しているのかに注意する必要があります。
光の強度とは何か
大雑把なイメージ
光の強度とは、大雑把に言うと、単位時間・単位面積あたりを流れるエネルギーの量のことです。ある方向に向いた光線のうちの、ある波長の成分のみに注目します。別の言い方をすると、ある方向を向いた光線に属する光子のうち、特定の波長を持つもののみに注目して、他の波長の光子は無視します。
このとき、光線に垂直な面を単位面積・単位時間あたりに通り抜ける光のエネルギー量が放射強度 (specific intensity) \(I_\lambda\) に相当します ( 図 10 )。より厳密な定義は後から説明します。上で説明したスペクトルとは、各波長 \(\lambda\) における強度 \(I_\lambda\) を表示したグラフです。
光子の持つエネルギー
光子 1 個が持つエネルギーはその光子の波長に反比例します。つまり、例えば波長 400 nm の光子が持つエネルギーは、 800 nm の光子が持つエネルギーの 2 倍です。具体的には、光子が持つエネルギー \(E\) は次のように書けます。
\begin{align} E &= \frac{hc}{\lambda} \\ \text{ただし},\quad h &= 6.63 \times 10^{-34} \ \text{J s} \\ &: \text{プランク定数} \\ c &= 3.00 \times 10^8 \ \text{m/s} \\ &: \text{光速} \\ \lambda &: \text{その光子の波長 [m]} \end{align}
例えば、波長 500 nm の光子が持つエネルギーは \(4.0 \times 10^{-19} \ \text{J}\) です。参考までに、これは約 2 万 K ( ケルビン 脚注 [ケルビン]：温度の単位には基本的にケルビン (K) を用います。日常で使われる摂氏と目盛の幅は同じであり，摂氏 0 度は 273.15 K です。つまり，例えば 300 K は摂氏 26.85 度のことです。 ) の温度の気体を構成する粒子 1 個が平均的に持つ運動エネルギーに相当します。あるいは、水素のイオン化エネルギー (水素原子 1 個から電子を剥がすのに必要なエネルギー) は \(2.2\times 10^{-18} \ \text{J}\) です。
図 10 と同じように、特定の方向に進む光子の集団 (光線) に属する光子のうち、特定の波長 \(\lambda\) を持った光子のみに注目します。伝搬方向に垂直な面を単位時間・単位面積あたりに通り抜ける光子数を \(n\) [\(\text{m}^{-2}\text{s}^{-1}\)] と書くことにします。数密度フラックスと呼ばれる量です。
単位面積を単位時間に通り抜けるエネルギー \(E/(S\delta t)\) は 図 11 のように、通り抜ける光子数と光子 1 個が持つエネルギーの積です。よって、放射強度と光子の数密度フラックスの間には次の関係があることが分かります。
\[I_\lambda \propto \frac{n}{\lambda}\]
特定の波長の成分に注目した場合、光線の強度はその光線に属するその波長の光子の数密度フラックスに比例します。ただし、同じ数密度フラックスの光線でも、波長によって強度は違います。波長の長い光子が持つエネルギーは小さいので、波長の短い光線の場合よりも強度が小さくなります。これが光の強度と光子数の大雑把な関係です。
放射強度の正確な定義
光の強度に関係する量の呼び方は、分野によって違うようです。天文学における放射強度 (specific intensity) とは次の量です。例えば日本天文学会が運用している 天文学辞典 の「放射強度」の項目を参照してください。
上の大雑把な説明では「ある方向を向いたある波長の光」に注目しました。厳密な話をすると、エネルギー量や光子数の議論をする際に、「特定の」方向や波長に注目するのは物理的ではありません。
正確には、特定の方向を含む微小な
立体角
脚注
[立体角]：立体角とは、簡単にいうと、2 次元的な角度のことです。2 つの直線のなす角度 (単位：ラジアン [rad]) が \(\theta\) のとき、この直線が張る半径 1 の円弧の長さは \(\theta\) になるのでした。これに対応して、ある錐体のなす立体角 (単位：ステラジアン [sr]) が \(\Omega\) のとき、この錐体と半径 1 の球面との交線がつくる面積は \(\Omega\) になります。全方向を見込む立体角は \(4\pi\) であり、地平線より上にある部分 (全方向の半分) を見込む立体角は \(2\pi\) です。
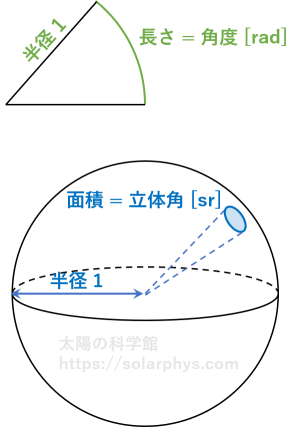\(d\Omega\) の範囲に伝搬する、 \(\lambda\) から \((\lambda+d\lambda)\) の間の波長を持つ光子のみに注目します。
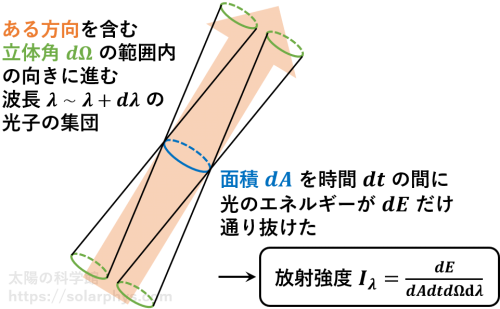
注目している光子の集団によって、微小時間 \(dt\) の間に微小な面積 \(dA\) を通り抜けて運ばれたエネルギー量を \(dE\) と書いたとき、放射強度 \(I_\lambda\) [単位 \(\text{W m}^{-2}\text{sr}^{-1}\text{m}^{-1}\)] は 図 12 のように定義されます。別の言い方をすると、放射強度とは、単位時間・単位面積・単位立体角・単位波長あたりに運ばれる光のエネルギー量です。
図 11 で説明したように、注目している光子の数密度フラックスを \(n\) とすると、
\[\frac{dE}{dAdt}=n\cdot \frac{hc}{\lambda}\]
と書けるため、\(n\) は \(I_\lambda\) を用いて次のように書けます。
\[n = \frac{I_\lambda \lambda d\lambda d\Omega}{hc}\tag{1}\]
太陽光の明るさの概算
詳しくは 黒体放射の記事 で説明していますが、観測衛星が地球大気の外で太陽から受け取る光のスペクトルは、 \(T=5800 \ \text{K}\) の黒体放射に近似できます。黒体放射とは、次のような放射強度の光のことを言います。
\begin{align} I_\lambda = \frac{2hc^2}{\lambda^5}&\frac{1}{\exp[hc/(\lambda k_BT)]-1} \tag{2}\\ \text{ただし},\quad k_B &= 1.38 \times 10^{-23} \ \text{J K}^{-1} \\ &: \text{ボルツマン定数}\end{align}
\(\exp x\) とは指数関数 \(e^x=(2.71\cdots)^x\) のことです。このことを用いて、地球で受け取る太陽光の強さを概算してみます。
観測衛星が太陽光線に垂直な面で単位時間・単位面積あたりに受け取る光のエネルギー量を放射照度 (irradiance) [単位 \(\text{W m}^{-2}\)] と言います。図 12 の定義に従うと、これは
\[\frac{dE}{dAdt}=I_\lambda d\Omega d\lambda\]
に相当する量です。ただし、今は特定の波長付近の光子だけではなく、全波長の光子が運ぶエネルギーに注目するので、上式を全波長で合計 (積分) した次の量を考えます。
\[S=d\Omega\int_0^\infty I_\lambda d\lambda\tag{3}\]
地球から見た太陽は円盤状です。太陽を見込む立体角 \(d\Omega\) は 図 13 のようにして計算できます。
\begin{align} d\Omega &\simeq \pi\left(\frac{R_\odot}{d}\right)^2 \tag{4}\\ \text{ただし},&\quad R_\odot = 7.0 \times 10^8 \ \text{m} \\ &\quad d = 1.5\times 10^{11} \ \text{m}\end{align}
式 (3) に 式 (2) と 式 (4) を代入し、積分変数を \(x=hc/(\lambda k_BT)\) と変換して式変形すると、次の式を得ます。
\[S=2\pi hc^2\left(\frac{R_\odot}{d}\right)^2\left(\frac{k_BT}{hc}\right)^4\int_0^\infty \frac{x^3}{e^x-1}dx\]
積分公式
\[\int_0^\infty\frac{x^n}{e^x-1}dx=n!\cdot \zeta(n+1)\tag{5}\]
と、リーマンゼータ関数の値が \(\zeta(4)= \pi^4/90\) であることを用いると、放射照度 \(S\) は最終的に次のように書けます。
\begin{align}S &= \sigma T^4\left(\frac{R_\odot}{d}\right)^2 \\ \text{ただし},\quad \sigma &= \frac{2\pi^5k_B^4}{15h^3c^2} \\ &= 5.67 \times 10^{-8} \ \text{W m}^{-2}\text{K}^{-4} \\ &: \text{シュテファン-ボルツマン定数}\end{align}
上述した黒体放射の有効温度 \(T=5800 \ \text{K}\) とは、およそ太陽表面の温度と考えられます。上式より、黒体放射をする物体の明るさは表面温度の 4 乗に比例することが言えます。これはシュテファン-ボルツマンの法則と呼ばれるものです。
上式に具体的な値を代入して計算すると、\(S= 1.4 \times 10^3 \ \text{W m}^{-2}\) という結果になります。面積 \(1 \ \text{cm}^2\) の面が 1 秒間に受け取るエネルギーは \(0.14 \ \text{J}\) です。参考までに、これは \(1 \ \text{cm}^3\) の水の温度を 30 ℃ 程度上昇させるのに必要なエネルギーです。
観測衛星が地球大気の外で測った太陽光の放射照度は太陽定数と呼ばれます。太陽定数の実測値は \(1.37\times 10^3 \ \text{W m}^{-2}\) です ( Fröhlich & Lean, 2004 )。記事「11 年周期：太陽の睡眠サイクル」で説明している太陽周期に伴って、太陽定数は約 11 年の周期で 0.1 % 程度変化します。太陽光の一部は地球大気で反射・吸収されるため、地上に降り注ぐ光の照度は太陽定数の何割かになります。
太陽から飛来する光子数の概算
今度は太陽から地球に飛来する光子の数密度フラックスを見積もってみます。式 (1) の \(n\) は波長 \(\lambda\) から \((\lambda + d\lambda)\) の間の波長を持つ光子のみに注目したときの量でしたが、今は目に見えない波長の光子まで含め、とにかく太陽から地球に飛来する光子全ての数密度フラックスを考えます。つまり、式 (1) を全波長に渡って合計 (積分) したものを考えます。
\[n=\frac{d\Omega}{hc}\int_0^\infty I_\lambda \lambda d\lambda \tag{6}\]
式 (6) に 式 (2) と 式 (4) を代入し、積分変数を \(x = hc/(\lambda k_BT)\) と変換して式変形すると、次のようになります。
\[n = 2\pi c \left(\frac{R_\odot}{d}\right)^2\left(\frac{k_BT}{hc}\right)^3\int_0^\infty\frac{x^2}{e^x-1}dx\]
再び 積分公式 (5) と、リーマンゼータ関数の値が \(\zeta(3)\simeq 1.2\) であることを用いると、光子の数密度フラックスは次のように書けます。
\[n = 4.8\pi c\left(\frac{R_\odot}{d}\right)^2\left(\frac{k_BT}{hc}\right)^3\]
ここに具体的な値を代入して計算すると、\(n = 6\times 10^{21} \ \text{m}^{-2}\text{s}^{-1}\) が出てきます。つまり、太陽光は、1 秒かつ \(1 \ \text{cm}^2\) の面積あたりに \(10^{17}\) 個程の光子が飛来しているのに相当する明るさです。一部は地球大気に反射・吸収されるため、地上に届く数はより少ないですが、桁違いに小さいわけではありません。
参考文献
記事全体として参考にした書籍
- Rybicki, G. B. and Lightman, A. P. (1985). Radiative Processes in Astrophysics (Weinheim: Wiley-VCH ).
- サクライ, J. J. (2010). 『サクライ上級量子力学〈第 1 巻〉輻射と粒子』 (樺沢宇紀訳, 東京: 丸善プラネット).
- 砂川重信. (1999). 『理論電磁気学』 (東京: 紀伊國屋書店).
引用した文献
- Fröhlich, C. and Lean, J. (2004). Solar radiative output and its variability: evidence and mechanisms. The Astronomy and Astrophysics Review, 12, 273–320 .