基本構造

基本的なプロフィール

太陽の基本的な量と、それがどのように求められるのかを簡単に説明します。

地球からの距離

地球が太陽の周りをどのように回っているのかは、地球から見える太陽や他の天体の位置を観測することで調べられるので、地球と太陽の間の距離は分かっています。その距離は約 1 億 5000 万 km です。

地球は楕円を描いて公転しているので、この距離は 1 年の中で変化します。太陽に近いときは 1 億 4700 万 km 程度、遠いときは 1 億 5200 万 km 程度です。平均的な距離

\[1 \ \text{au} = 1.50 \times 10^{11} \ \text{m}\]

は天文学分野で使われる距離の単位の 1 つになっていて、「 天文単位 脚注 [天文単位 (au)]：距離の単位です。1 au = 1 億 5000 万 km は地球と太陽の間の平均的な距離です。 1 au = 215 太陽半径であり、1 光年 = 63,000 au です。他に、地球と月の間の距離は 0.0026 au、海王星の軌道半径は 30 au 程度です。 (au)」と呼ばれます。

太陽と地球の間の距離は、太陽半径の 200 倍程度です。太陽で発せられた光が地球に到達するまでには 8 分 20 秒かかります。

半径

地球から見える太陽表面 ( 光球 脚注 [光球]：フィルターを通さずに可視光で観測したときに明るく映る層のことです。大雑把にはこの層が「太陽表面」と呼ばれます。より細かくは高度 0 から 500 km あたりの層を言います。 ) の半径は、見込む角度 (視半径， 図 1 参照) にして 16 分角程度です。1 分角とは、1 度の 1/60 の大きさの角度です。参考までに、腕をいっぱいに伸ばしたとき、拳 (手の幅) を見込む角度が大体 10 度と言われます。月は太陽表面と大体同じ大きさに見えています。

太陽の視半径も、地球からの距離が変化するのに伴って 15.8 から 16.3 分角程度まで変化します。地球からの距離は先ほど述べたようにして分かっているので、太陽の実際の半径を求めることができます。その値は次の通りです。

\[R_\odot=6.96\times 10^{8} \ \text{m}\]

約 70 万 km と覚えてください。これは地球半径の約 100 倍です。例えば地球が卓球ボールの大きさだとしたら、太陽は約 1 km 先にある直径 4 m の球です。あるいは、太陽がサッカーボールの大きさだとしたら、地球は約 50 m 離れた場所にある 2 mm のゴマ粒です。

質量

惑星が太陽の周りをどのような軌道を描いて公転しているのかは、地上から見える惑星の動きを観測することによって、かなり正確に調べることができます。その情報からケプラーの法則を用いれば、重力定数 \(G\) と太陽質量 \(M_\odot\) の積 \(GM_\odot\) が計算できます。重力定数は別の実験からそこそこの精度で決定されているため、\(M_\odot\) 自身も求めることができます。求まっている値は次の通りです。

\[M_\odot=1.99 \times 10^{30} \ \text{kg}\]

これは地球の質量の約 30 万倍です。太陽系でいちばん質量の大きい惑星は木星ですが、その木星と比べても約 1000 倍あります。因みに、地球表面での重力加速度は \(9.8 \ \text{m/s}^2\) ですが、太陽表面では \(274 \ \text{m/s}^2\) です。

明るさ (光度)

太陽の明るさをきちんと調べるには、人工衛星を用いての観測が必要です。地球に降り注ぐ太陽光の一部は地球の大気に吸収されたり反射されたりするので、地上の観測データを素朴に解釈すれば過小評価になります。

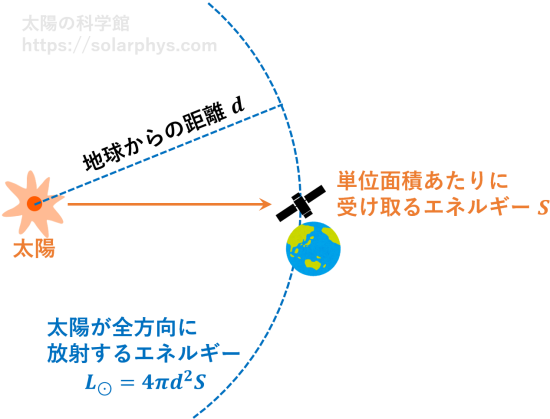
観測衛星が単位面積、単位時間あたりに受ける太陽光のエネルギーは \(S = 1.37\times 10^{3} \ \text{W/m}^2\) です。これは太陽定数と呼ばれます。太陽は全ての方向に等しい強度の光を放っていると仮定すれば、 \(S\) に地球と太陽間の距離 \(d\) を半径とする球面の面積を乗じることで、太陽が単位時間あたりに光として失っているエネルギー量が計算できます ( 図 2 )。

\[L_\odot=4\pi d^2S=3.86 \times 10^{26} \ \text{W}\]

これは太陽光度と呼ばれます。太陽光の観測はまだ地球の近傍でしか行われていないため、上の仮定がどの程度正しいかは分かりません。記事「11 年周期：太陽の睡眠サイクル」で説明している太陽周期に伴って、太陽定数は 11 年の周期で 0.1 % 程度変化します ( Fröhlich & Lean, 2004 )。

太陽内部の基本構造

太陽は地球と同じような岩石、あるいはマグマでできていて、燃えているといったようなイメージを持たれている方が少なからずいるかもしれませんが、そのイメージは間違いであると言わざるを得ません。

太陽は主に水素とヘリウムから成る気体です。気体が自らの重力によって集まり、球形をなしています。内側にいくほど上に積み重なっている気体の量が多くなるため、より圧縮されて密度や圧力が高くなっています。これを 重力成層 脚注 [重力成層]：下向きに重力がかかっているところに気体が積み重なると、下の気体は上に乗っている気体に押しつぶされて密度や圧力が高くなります。このように、上に行くほど密度や圧力が低くなるように気体が積み重なった状態を重力成層と言います。地球の大気も重力成層しているため、高い山に登ると空気が薄くなります。 と言います。地球大気も重力成層をしているため、高い山に登ると気圧が低くなり、空気が薄くなります。そのような物理的状況が中心部まで続いているのが太陽です。

これはこの記事でいちばん強調したいことなので、もう一度述べます。太陽は気体の塊です。宇宙空間に \(10^{30} \ \text{kg}\) もの大量の物質が存在していると、重力によって互いに引き合い、一点を中心として集まってきます。集まった気体は重力と圧力がつり合うことで、一定の形を保ちます。そのときに取るいちばん単純な形は、角のない球形です。太陽表面は綺麗な球形をしています。

密度

図 3 に赤色で太陽内部の質量密度の様子を示しました。これは「標準太陽モデル (standard solar model)」と呼ばれ、理論的に求まった値です。少なくとも数 % の精度では正しい値であることが観測に基づいて確認されています。どのように計算されるのかについては下の節で説明します。

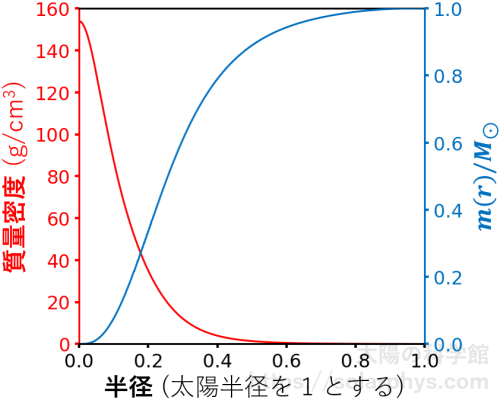
図を見ると、確かに中心に行くほど質量密度が高くなっています。表 4 に、太陽の各領域での典型的な密度の値と、身の回りの物質との比較を載せました。質量密度とは、\(1 \ \text{cm}^3\) あたりの質量 [\(\text{g}\)] であり、数密度とは、\(1 \ \text{cm}^3\) あたりに何個の粒子が存在するかです。

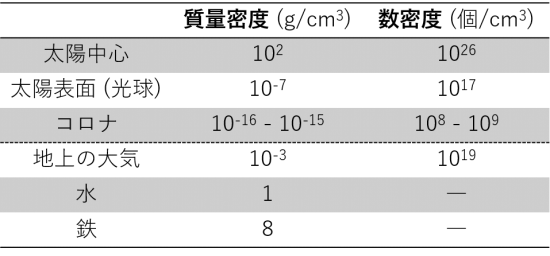
表の通り、太陽表面や コロナ 脚注 [コロナ]：高度数千 km より高層の大気を指します (太陽半径は約 70 万 km)。極端紫外線や X 線で見ることができます。 は地上の大気よりも密度が小さいです。太陽表面の半径を \(R_\odot\) として、半径 \(0.53 R_\odot\) あたりで水と質量密度が同じ (\(1 \ \text{g/cm}^3\)) になります。中心は鉄 の 20 倍近くの重さになります。それでも温度が高いために、結晶化せずに気体のままで存在しています。

図 3 に青色で示したのは、その半径より内側にある質量の合計です。太陽の総質量を 1 とした割合が示されています。太陽の質量の半分は半径 \(0.26R_\odot\) より内側にあります。半径 \(0.7R_\odot\) より内側にある質量は、総質量の 97 % です。これを見ると、太陽の質量のほとんどは内側半分に存在することが分かります。

温度と圧力

太陽は地球大気とは違って、高温です。太陽光を分析することで、太陽表面の温度は簡単に推定することができ、約 6000 K ( ケルビン 脚注 [ケルビン]：温度の単位には基本的にケルビン (K) を用います。日常で使われる摂氏と目盛の幅は同じであり，摂氏 0 度は 273.15 K です。つまり，例えば 300 K は摂氏 26.85 度のことです。 ) であることが分かっています。詳しくは記事「黒体放射：なぜ明るいのか？」で説明しています。参考までに、コンロの炎は 2000 K 程度です。

図 5 に赤色で温度の構造を示しました。内側にいくほどどんどん温度は高くなり、中心では 1500 万 K 程度になっています。

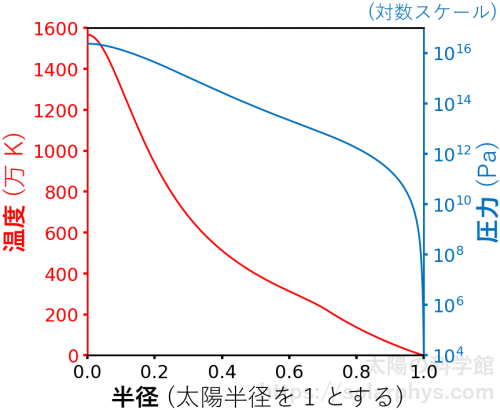
図 5 に青色で示したのは圧力の構造です。太陽は気体であると述べましたが、太陽を構成する物質は基本的には理想気体の状態方程式

\begin{align} p &= nk_BT \\ \text{ただし}, &\quad p: \text{圧力 [Pa]} \\ &\quad n: \text{数密度 [/m}^3\text{]} \\ &\quad k_B = 1.38 \times 10^{-23} \ \text{J/K} \\ &\quad \qquad: \text{ボルツマン定数} \\ &\quad T: \text{温度 [K]}\end{align}

に従います。化学の授業では \(PV=NRT\) という形式で習う法則です。図で示しているような標準太陽モデルの計算では、様々な要因による上式からのずれも考慮されていますが、大雑把には上式の関係が成り立っています。つまり、高温である太陽は、圧力もまた高くなっています。

太陽表面での圧力は \(10^4 \ \text{Pa} = 0.1\) 気圧程度ですが、内部に行くと圧力は高くなり、中心部では \(10^{16} \ \text{Pa} = 10^{11}\) 気圧程度になっています。

上で説明したのは太陽内部の温度構造です。一方で、太陽大気、つまり表面より外側の部分は表面よりずっと熱く、100 万 K 程度になっています ( 図 10 参照 )。そのような高温になっている原因については、まだ解明されていません。太陽大気の温度構造については、記事「コロナ加熱：温度構造がおかしい？」で説明しています。

物質の組成

質量存在比

地球に降り注ぐ太陽光のうちの特殊な波長 (色) の成分 ( 吸収線 脚注 [吸収線]：太陽からの光をスペクトル分解 ( = 各波長ごとの強度を表示) すると、周りと比べて強度の弱い波長帯が所々に現れます。これを吸収線と言います。逆に、どの吸収線にも該当しないような波長の光を連続光と言います。 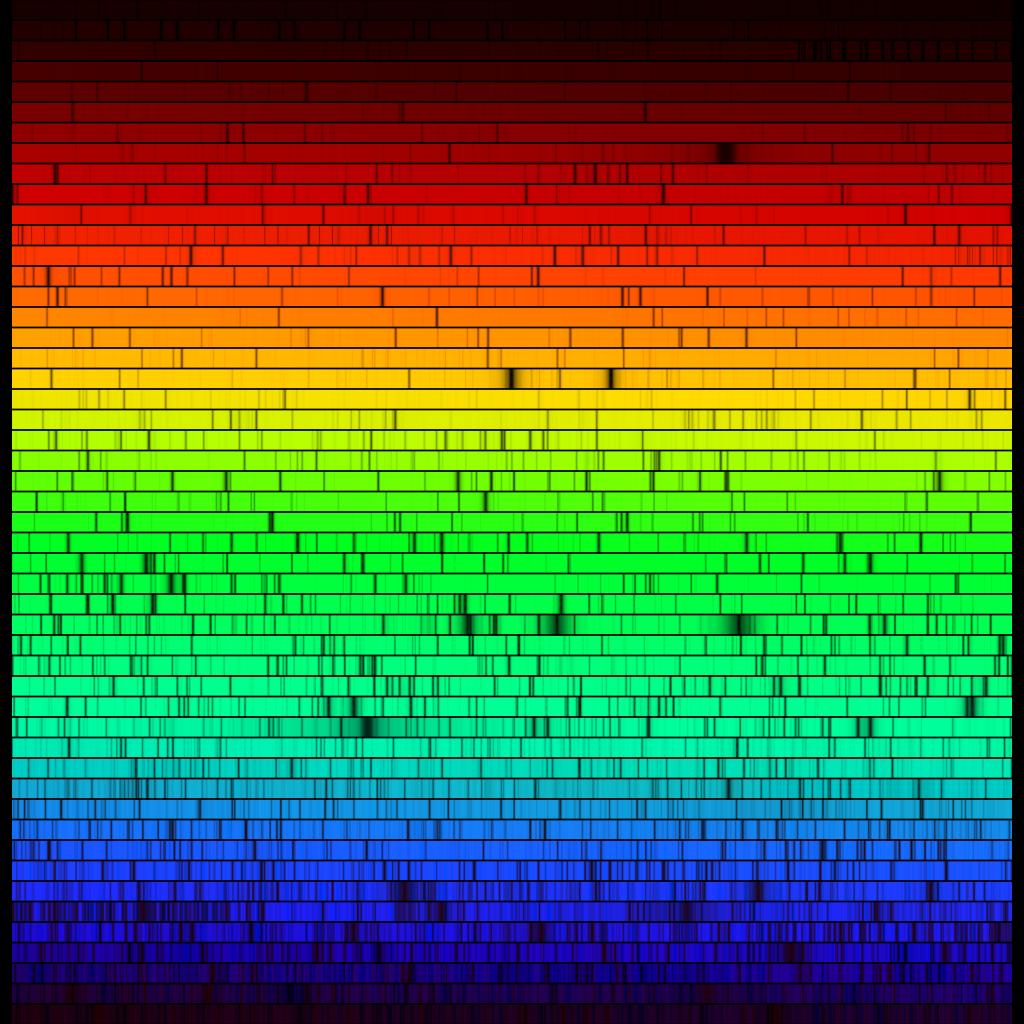図：太陽光を各波長 (色) ごとに分解したもの。黒く見える波長が吸収線。提供 N.A.Sharp, NOAO/NSO/Kitt Peak FTS/AURA/NSF ) を観測して分析することで、光が放たれる場所である太陽表面に含まれる様々な元素の量を推定することができます。ただし、ヘリウムやネオンなどの希ガス (貴ガス) はこの手法での推定は難しく、別の手法によって決定されます。詳しくは下の節で説明します。

そうして求まった太陽表面の組成を 図 6 に示しました。質量にして何 % 含まれているかを表しています。太陽表面は主に、73 - 74 % の水素と、25 % のヘリウムでできています。その他の元素は残りの 1 - 2 % を占めます。

「その他」の元素の含有率は、細かい話をすると、研究によって 1.3 % - 2.0 % 程度のばらつきがあります。このばらつきが現在引き起こしている問題を下の節で紹介します。

標準太陽モデルによって求まっている太陽内部の組成を 図 7 に赤色で示しました。水素 7 割ちょっと、ヘリウム 2.5 割の比率は大雑把に半径 \(0.3R_\odot\) まで続いています。

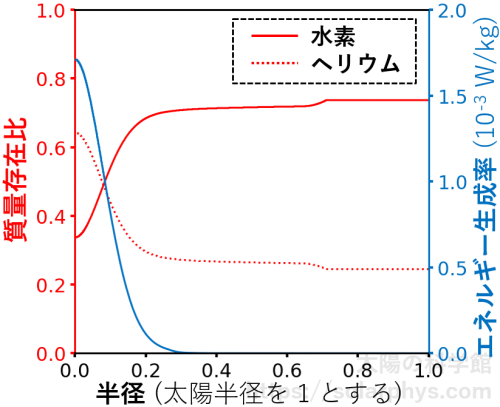
一方で、半径 \(2R_\odot\) 以内の中心部では、水素の比率が減って、ヘリウムが増えています。これは、中心部で核融合が起きているからです。詳しくは記事「ニュートリノ問題：エネルギー源は何？」で説明していますが、核融合反応では水素が使われて、ヘリウムが生成されます。それに伴って大量のエネルギーも解放されるため、中心部は常に加熱されています。核融合によるエネルギー発生率が 図 7 に青色で示されています。

具体的な状態

太陽は主に水素とヘリウムから成ると述べました。実験室にある水素は、水の電気分解で生成され、火をつけると爆発する気体です。また、身の回りにあるヘリウムは、宙に浮く風船の中に入っていたり、吸ったら声が高くなるジョークグッズに用いられる気体です。

太陽は高温なので、水素やヘリウムは、上述したような、我々が目にする状態とは違った状態で存在します。日常の環境での水素とヘリウムは、それぞれ \(\text{H}_2\) 分子と \(\text{He}\) 原子が飛び交う状態で存在します。これらは電気的に中性の (電荷を持たない) 粒子です。温度が高くなると、原子核と電子は 図 8 のように 電離 脚注 [電離]：粒子が電子を手放して電荷を持つようになることを電離と言います。電荷を持った粒子を含む気体をプラズマと言います。一部の粒子のみが電離している状態を部分電離または弱電離と言います。 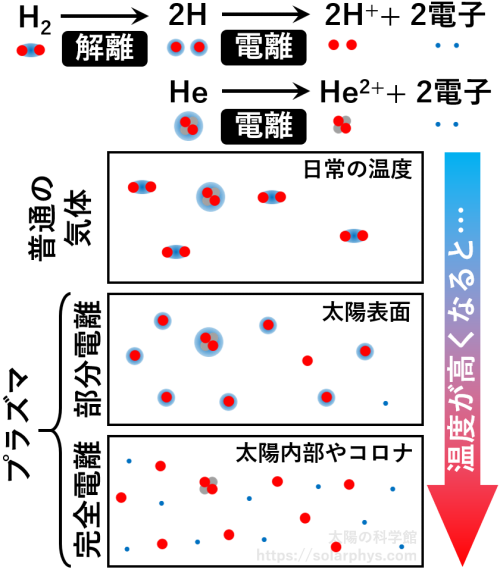して、それぞれ電荷を持った粒子として独立して存在するようになります。

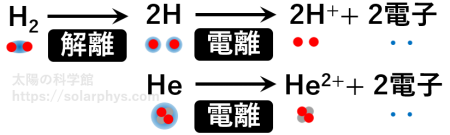
どの温度で電離するかは気体の密度にもよるので、一概には言えませんが、太陽内部やコロナの高温では、ほぼ全ての水素とヘリウムが電離した状態で存在します ( 図 9 の下段 )。これは完全に電離した状態と呼ばれます。

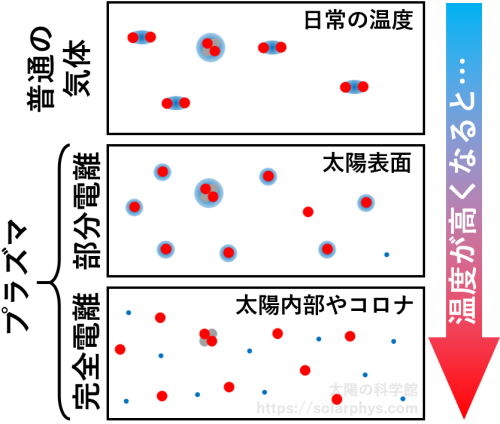
一方で、太陽表面はちょうど 図 8 の電離が起きるか起きないかの瀬戸際の温度です。そのため、太陽表面では、ほとんどの粒子は原子核と電子が結合した状態で存在し、ごく一部の粒子だけが電離しています ( 図 9 の中段 )。これは部分的に電離した状態と呼ばれます。

図 10 に太陽表面付近の電離状態の様子を、温度や質量密度と共に示しました。横軸は半径で、表面の半径を 1 とした値です。大体半径 \(0.97 R_\odot\) より外側かつ \(1.006R_\odot\) より内側の領域では、水素やヘリウムが部分電離の状態になっています。Leenaarts et al. (2007) の計算によると、 光球 脚注 [光球]：フィルターを通さずに可視光で観測したときに明るく映る層のことです。大雑把にはこの層が「太陽表面」と呼ばれます。より細かくは高度 0 から 500 km あたりの層を言います。 の水素は大雑把には 1 万個に 1 個が電離した状態です。

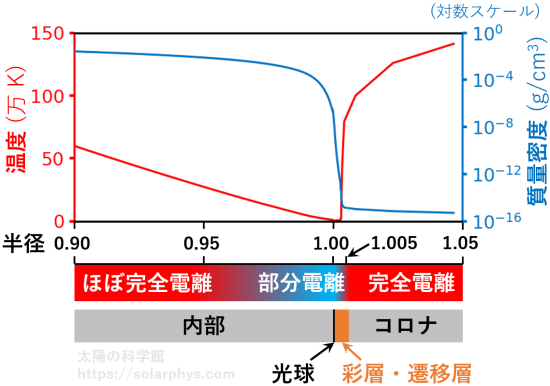
太陽大気 (表面より外側の領域) のうち、光球の少し上の領域は 彩層 脚注 [彩層]：太陽大気のうち、高度 500 km から数千 km の層を指します (太陽半径は約 70 万 km)。太陽表面より少しだけ上の領域と考えてください。例えば波長 656.3 nm (Hα 線) や 396 nm (Ca H 線)、 30.4 nm の光などで観測すると見ることができます。 と呼ばれます。この領域では、① 気体が薄い、② 部分電離の状態にある、③ 中途半端に不透明 の 3 要素が揃っているために、シミュレーションを行うのが難しく、まだ理解されていない部分が多い領域です。記事「太陽七変化：様々な光で見た姿」でも一部を紹介していますが、この領域では複雑な現象がたくさん観測されており、現在熱心に研究が行われています。

図 9 に記したように、電荷を持った粒子を含む気体を「プラズマ (plasma)」と言います。詳しくは記事「プラズマとは何か？：宇宙の基本要素」で説明していますが、プラズマは電気を通しやすいという性質を持ちます。別の言い方をすると、電気抵抗が物凄く小さいということです。これは太陽が起こす現象を考えるうえで非常に重要な性質です。他の記事の説明でも度々この性質がキーポイントになります。

エネルギーの流れ

太陽内部は中心から外側に行くほど温度が低くなる構造をしていると述べました。一般的に、エネルギーは温度の高い方から低い方へと流れる性質があります。太陽は常に輝くことで、表面から光としてエネルギーを失っています。それを補うように、中心部から表面までのエネルギーの流れが存在します ( 図 11 )。そして、その流れの源泉は中心部での核融合反応です。

太陽内部でエネルギーが具体的にどのように流れているのかを説明します。半径 \(0.7R_\odot\) 以内の領域では「放射輸送 (radiative transfer)」、\(0.7R_\odot\) より外側の領域では「熱対流 (thermal convection)」と呼ばれる方式によってエネルギーが流れています。それぞれの領域を放射層、対流層と言います。

熱対流

対流層では、 熱対流 脚注 [熱対流]：水の入った鍋を下からコンロで熱すると、熱くなった底付近の水は軽くなって上方へ移動します。逆に元々鍋の上方にあった水は熱せられた水と比べて重いため、下方へ移動します。これの繰り返しによって、鍋の中の水は温度を一様にしようとします。これが熱対流です。エネルギーの観点では、下からコンロによって加えられる熱エネルギーを熱対流が上方へ輸送していることになります。 によってエネルギーが上向き (表面に向かう向き) に運ばれています。熱対流とは、気体の動きによってエネルギーを輸送する現象です。

図 12 で示したように、太陽内部は下向きに重力がかかり、上に行くほど温度が低い状態にあります。太陽表面は光としてエネルギーが逃げて行くことによって、常に冷やされています。冷えた気体は周囲より重くなるので、重力に従って下に移動します。それを補うために周りの気体は上に移動します。このようにして、対流層内部は暖かい気体が上に、冷たい気体が下に向かって移動する傾向にあります。つまり、正味として熱が上向きに輸送されていることになります。

太陽表面で観測される熱対流については記事「粒状斑：太陽表面での対流」、内部の熱対流については記事「差動回転：回り方がおかしい？」で説明しています。対流層内部の熱対流が具体的にどのような流れをしているのかについては、まだ分からないこともあります。

放射輸送

放射層では、 放射輸送 脚注 [放射輸送]：太陽を構成するプラズマは高温なので、通常の熱伝導や熱対流に加えて、光を放出したり、近くで放出された光を吸収したりすることによって運ばれるエネルギーも無視することができません。これを放射輸送と言います。周りの物質分布や温度などの情報から、各場所での光の強度を計算するための方程式を放射輸送方程式と言います。 によって、エネルギーが上向きに運ばれます。放射輸送とは、光を媒介してエネルギーが輸送される現象です。

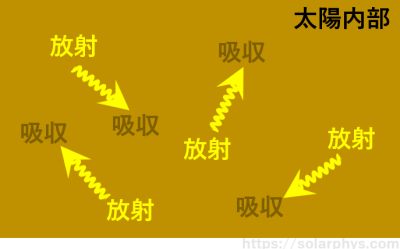
詳しくは 黒体放射の記事 で説明していますが、太陽内部の気体は温度が高いため、光を発しています。ある部分が発した光はすぐに隣の部分に吸収されます。この光の放射と吸収の連続が常にあらゆる場所で起きています ( 図 13 )。存在する光のエネルギー量、つまり明るさは、その場所の温度の 4 乗に比例します。

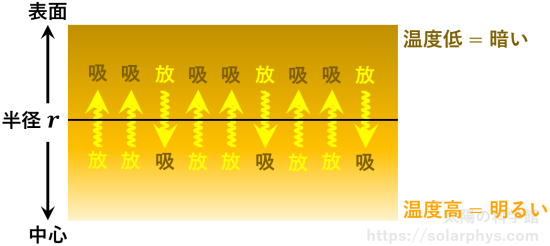
太陽内部は内側に行くほど温度が高いため、内側ほど光の量が多くなっています。図 14 のように、中心からの距離 (つまり半径) が一定値 \(r\) の面に注目します。この面を挟んで下側の方が、上側よりも高温です。よって、この面を下から上に横切る光の量の方が、上から下に横切る光よりも多くなります。これは、正味としてエネルギーが上向きに運ばれていることを意味します。

放射層と対流層を分かつ物理

太陽内部の半径 \(0.7R_\odot\) より内側の領域では放射輸送によってエネルギーが運ばれ、外側の領域では熱対流によって運ばれていると述べました。なぜ内側と外側でエネルギーの輸送形態が異なるのか、この \(0.7R_\odot\) という境界を決めている物理は何なのか、説明します。

太陽内部は中心から外側に向かうにつれて温度が下がります。その下がり方がどれだけ急かに注目します。具体的には次の量を考えます。

\[\frac{dT}{dr}\]

これは、横軸を半径 (中心からの距離) \(r\)、縦軸をその半径での温度 \(T (r)\) としたグラフを書いたときの傾きであり、温度勾配と言います。基本的に \(r\) が大きくなる程 \(T(r)\) は小さくなるため、温度勾配は負の値を取ります。その絶対値が大きいほど、その場所での温度の下がり方が急であることを表します。

対流の発生条件

温度勾配の絶対値が小さい (温度の下がり方がなだらかな) 場合には、熱対流は起きません。これがある値を超えると、熱対流が発生します ( 図 15 )。その閾値を断熱温度勾配と言います。

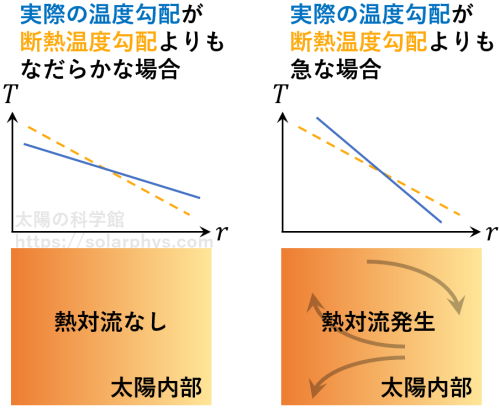
天気予報で「今日は大気の状態が不安定です」という言葉を耳にすると思います。これは、その日の大気の温度勾配が断熱温度勾配より急であることを言っています。そういった日には、大気で対流が起き、それに伴う上昇流で雲が作られ、天気が悪化します。

放射輸送に必要な温度勾配

放射輸送によって運ばれるエネルギー量は温度勾配に依存します。太陽内部のある場所で水平な面を考えたとき、その面を放射輸送によって単位時間・単位面積あたりに、内側から外側に通り抜けるエネルギー量 \(F_\text{rad}\) は、次のように書けます。

\begin{align} F_\text{rad} &= \frac{16\sigma}{3} \frac{T^3}{\rho\kappa}\frac{dT}{dr} \\ \text{ただし}, \quad \sigma &= 5.67\times 10^{-8} \ \text{W m}^{-2}\text{K}^{-4} \\ &: \text{シュテファン-ボルツマン定数} \\ T&: \text{温度 [K]} \\ \frac{dT}{dr}&: \text{温度勾配 [K/m]} \\ \rho&: \text{質量密度 [kg/m}^3\text{]} \\ \kappa&: \text{不透明度 [m}^2\text{/kg]}\end{align}

温度勾配が大きいほど、ある面を挟んだ上下での明るさの違い ( 図 14 参照 ) が大きいので、エネルギー輸送の効率は良くなります。よって \(F_\text{rad}\) は \(dT/dr\) に比例します。

\(F_\text{rad}\) は \(T^3\) にも比例します。つまり、温度が低くなると、放射輸送の効率は劇的に落ちます。これは光の量が少なくなるからです。

もうひとつ上式で注目すべき点は、\(F_\text{rad}\) が \(\kappa\) に反比例することです。これは「不透明度 (opacity)」と呼ばれる量で、文字通り、その場所で光がどれだけ気体を透過できないか ( = どれだけすぐに吸収されてしまうか) の度合を表します。気体がより不透明なほど放射輸送の効率は悪くなります。

前述したように、太陽の表面付近は部分電離の状態にあります。表面まで行かなくとも、比較的浅い (表面に近い) 領域では、稀に電離していない水素原子やヘリウム原子が存在します。そしてその存在確率は表面に近づくほど増えていきます。

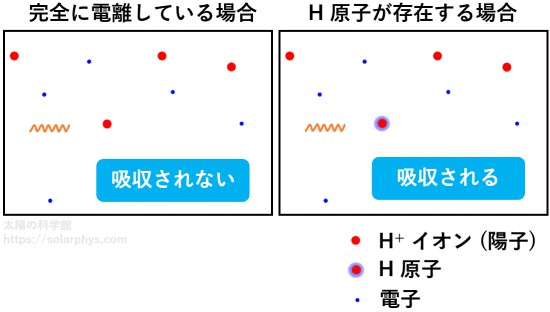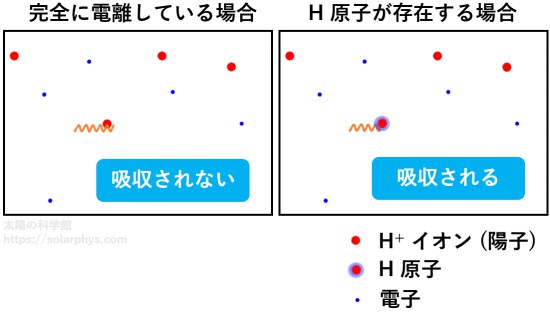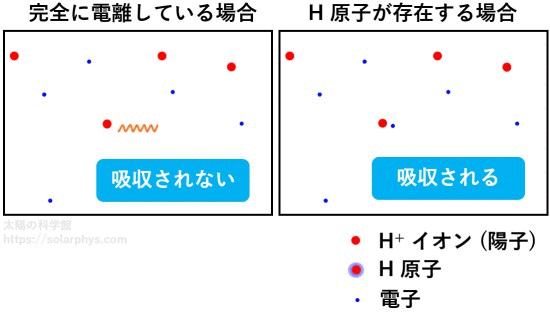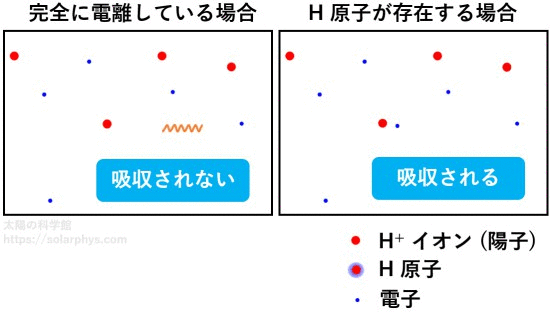
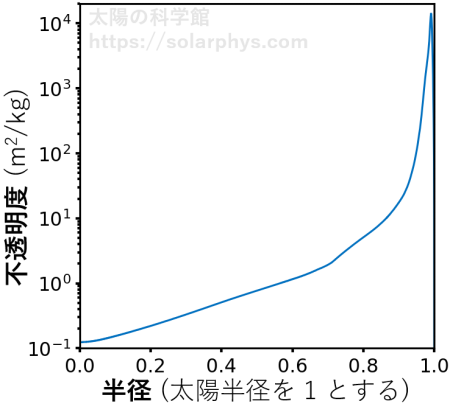
図 16 に示したように、電子を持った粒子は光を吸収して電離する反応を起こすことができます。そのため、未電離の粒子の存在率が大きくなると、気体はその分だけ光をより吸収しやすくなります。従って、太陽内部は表面に近づくと不透明度が劇的に大きくなります。その様子を 図 17 に示しました。

核融合が起きている中心部を除いて、各場所で上向きに運ばれるエネルギーは、水平方向で合計すると太陽光度 \(L_\odot\) に相当する量でなければなりません。でないとエネルギー収支のバランスが崩れてしまいます。

温度が低くなり、尚且つ不透明度が大きくなることで放射輸送の効率が悪くなると、同じだけのエネルギーを運ぶためには、より急な温度勾配が必要になります。つまり、表面に近づくと、放射輸送に必要な温度勾配の絶対値は大きくなります。

放射層と対流層

図 18 に、各半径で放射輸送によって \(L_\odot\) に相当するエネルギーを運ぶのに必要な温度勾配と、断熱温度勾配、実際に標準太陽モデル内で実現している温度勾配の 3 つの値を示しました。

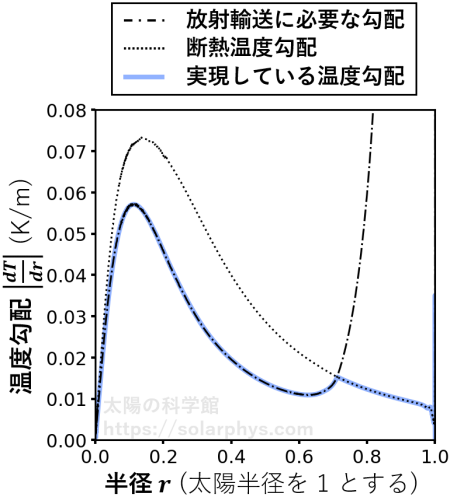
内側の領域では、放射輸送に必要な温度勾配が断熱温度勾配よりもなだらかであるため熱対流は起きず、放射輸送のみでエネルギーを上に伝えています。

先ほど述べたように、表面に近づくと、温度の低下と不透明度の増加に伴って放射輸送に必要な温度勾配の絶対値も大きくなります。そして、半径 \(0.7R_\odot\) 付近で断熱温度勾配を上回り、熱対流が発生します。いったん熱対流が起きると放射輸送より効率が良いため、エネルギーはほとんど熱対流によって運ばれることになります。

対流層内部は対流によってかき混ぜられることで温度勾配が均されているため、ほとんど断熱温度勾配を維持しています。図 18 をよく見ると、表面付近 (図の端) の温度勾配が大きくなっている様子が微妙に確認できます。表面は光としてエネルギーが逃げることで強く冷やされており、熱対流も激しくなっています。表面の温度勾配は例外的に断熱温度勾配を超えて急になっています。

他の恒星の場合

太陽は内側が放射輸送、外側が熱対流というエネルギー輸送の方式を取っていますが、夜空に浮かぶ恒星の全てが同じ構造なわけではありません。太陽と同じように、中心部で水素の核融合を起こしている星を「主系列星 (main sequence star)」と言います。しかし、同じ主系列星でも、その質量によってエネルギー輸送の形態は異なります ( 例えば Kippenhahn et al., 2012 )。

太陽より質量の小さい主系列星では、温度がより低いため、上述した仕組みに従って、外側の対流層が恒星の多くの部分を占めています。Kippenhahn et al. (2012) によると、質量が \(0.25M_\odot\) (\(M_\odot\) は太陽質量) を下回るような星では、全ての部分で熱対流が起きているようです ( 図 19 の左 )。

逆に、太陽より質量の大きな主系列星では、外側の対流層は無くなります。代わりに、中心部に対流層が形成されると考えられています ( 図 19 の右 )。重い星では、核融合が効率よく起きている領域が中心に集中しています。そのため、中心部で大量のエネルギーを外向きに運ぶ必要があり、温度勾配が急になっています。故に断熱温度勾配に達していて、熱対流が発生しています。

標準太陽モデル

これまで説明してきた太陽内部の構造は、標準太陽モデルと呼ばれる計算によって明らかにされたものです。標準太陽モデルにも、計算時に採用する物理の違いによってバリエーションがありますが、上の節で紹介したのは、 Christensen-Dalsgaard et al. (1996) のモデルです。これは現在よく分かっている物理をふんだんに取り入れて計算されたモデルであり、後に説明するように、とりあえず程よい精度で太陽内部を再現していることが別の手法から確認されています。

標準太陽モデルは、太陽内部で成り立つ物理法則の方程式を太陽誕生時から 46 億年分計算することで、現在の太陽内部の構造、ないしは太陽の過去と将来の姿を推測する手法です。具体的に何を計算しているのかについて説明します。

計算をするにあたっての仮定

大まかには次の 4 つの仮定をしたうえで、モデルを組み立てます。

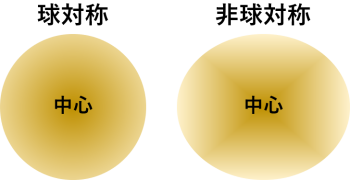
• 太陽は完全に球対称な系であると仮定します ( 図 20 )。つまり、水平方向に構造が変化している可能性は考えず、自転のような非対称の物理も考えません。熱対流も非球対称な現象ですが、これについては適当に簡略化して考慮します。

• 太陽の年齢は隕石の年代測定と太陽系初期のモデルを組み合わせることで、45.7 億年程度であると推定されています。Christensen-Dalsgaard et al. (1996) のモデルでは、計算開始から 46.0 億年後を現在の太陽としています。この期間を 45.7 億年に変えても、顕著な違いは現れないことが確認されています。
• 太陽全体の質量は終始 \(M_\odot = 1.99 \times 10^{30} \ \text{kg}\) であり、46 億年に渡って変化しないと仮定します。実際には太陽風が持ち去ることで、太陽は常に質量を損失していますが、この影響は 46 億年に渡ってもごく僅かであると考え、無視します。
• 太陽誕生時の組成 (水素、ヘリウム、その他の元素の存在比) は内部全体で一様であると仮定します。誕生時の太陽は全体で熱対流が起きていたと考えられるため、内部は良くかき混ぜられた状態であったと考えれば、この仮定は正当化されます。

計算時に解かれる方程式

球対称の仮定により、太陽内部の温度、質量密度、圧力、組成、上に運ばれるエネルギー量、不透明度のような物理量は全て中心からの距離 (半径) と時間の関数として表されます。これらの量の間の関係を 流体力学 脚注 [流体力学]：液体や十分に濃い気体の速度、温度、圧力や密度などの時間発展を計算するための理論を流体力学と言います。 や原子物理学からの知見を用いて規定し、全ての関係が常時満たされているようにして、内部の構造とその 46 億年間の変化をコンピュータで計算します。

具体的に解かれる流体力学的関係は次の通りです。

• 総質量: 質量密度を全体に渡って合計すると、\(M_\odot\) にならなければなりません。
• 力のつり合い: 太陽内部のある場所に注目したとき、その場所を挟んで上側よりも下側の方が高圧なため、その場所の気体は圧力差分の力を上向きに受けます。太陽が安定して存在するためには、その圧力差と重力がつり合っていなければなりません ( 図 21 )。

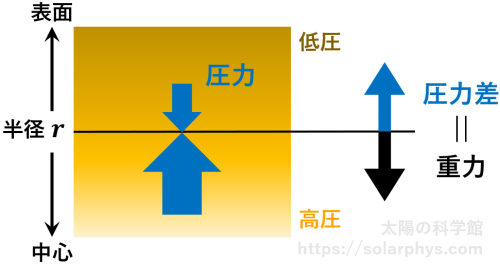
• エネルギーの保存: 核融合によってその場所より内側で生成された分だけのエネルギーが滞りなく上向きに運ばれなければなりません。エネルギーの輸送方式が放射か対流かの切り替えは、上述したように、放射輸送に必要な温度勾配が断熱温度勾配より急かどうかを判定基準にして行われます。
• 組成の変化: 内部の組成の変化が太陽の進化を司ります。上述した仮定より、計算開始時は内部全体で同じ組成をしていますが、核融合が起こると各元素は増えたり減ったりします。また、仮にある元素がとある場所に集中していたら、拡散が起きて広がっていきます。長い目で見ると、重い元素は重力によって沈下もします。これらの効果を取り入れて、各場所での組成の時間変化を追います。
• 表面の定義: 太陽表面とは、大雑把に言うと、それより外側は透明、内側は不透明となっている境界です。太陽大気についての別の研究から得られた関係を用いると、太陽表面が持つべき圧力などの状態が計算できます。それを満たす半径をその時の太陽半径 \(R\) とし、それ以内の領域の構造を上述した流体力学的関係を用いて毎時決定します。太陽半径は年齢と共に変化します。

組成が変化すると、その組成に応じて新たな内部構造や核融合の発生率、太陽半径、太陽光度が決まります。すると、それに応じてまた組成が変化します。この繰り返しを 46 億年分計算します。

具体的に計算を行うには、上述した関係だけでは足りず、原子レベルで起きている現象の考察や、熱対流が運ぶエネルギーについての考察が必要です。ここにどのような物理を盛り込んで計算するかが、標準太陽モデルのバリエーションを生みます。具体的には次の通りです。

• 状態方程式: 大雑把には理想気体の状態方程式が適用できると述べましたが、十分な精度の計算を行うにはそこからのずれも考慮する必要があります。例えば、プラズマは電荷を持った粒子の集まりなので、粒子間に働く クーロン力 脚注 [クーロン力]：同じ符号の電荷を持った粒子の間には、互いに離れようとする力が働き、逆符号の電荷を持った粒子間には近づこうとする力が働きます。これをクーロン力と言います。クーロン力は粒子間の距離の 2 乗に反比例します。 の影響もあります。あるいは、中心付近では密度が大きくなっているため、電子は他の電子の様子を伺いつつ、隙間を探して運動しなければならなくなってきます (部分縮退)。
• 不透明度の計算: 不透明度は、気体を構成する各粒子がどれだけ光を吸収しやすいかの合計で決まります。2 % 程度しか含まれない水素とヘリウム以外の元素によって不透明度は大きく左右されます。そのため、不透明度を計算するには、各元素の各電離状態ひとつひとつが光に及ぼす影響を丹念に調べる必要があります。
• 核融合の起きやすさ: ニュートリノ問題の記事 で詳しく説明していますが、核融合反応には大きく 2 つの反応経路があります。それぞれの反応の起きやすさは理論や実験から求められています。それをモデルに組み込むことで、中心部の温度や密度から核融合によって解放されるエネルギー量が計算されます。
• 組成の拡散の起きやすさ: 組成の時間変化の計算に必要である拡散の起きやすさも、原子の振る舞いについての考察から計算されます。
• 熱対流が運ぶエネルギー量: 熱対流は非球対称な現象であるため、何らかの簡略化をしてモデルに取り込まなければなりません。具体的には、熱対流によって運ばれるエネルギー量を計算する必要があります。差動回転の記事 で説明していますが、対流層で起きている熱対流の具体的な様式はまだ分かっていない部分が多いです。標準太陽モデルでは素朴な (現実的かは自明ではない) 考察に基づいて熱対流を取り入れていますが、その効率を決めるパラメータを何らかの方法で決定しなければなりません。

計算と調整

計算開始時 (太陽誕生時) の組成 \(X_0\) と熱対流の効率を決めるパラメータ \(\alpha\) を指定すれば、上述したようにして構築されたモデルの計算を実行することができます。 46 億年分計算した結果、現在の太陽光度 \(L_\text{now}\)、表面の組成 \(X_\text{now}\)、太陽半径 \(R_\text{now}\) がアウトプットされます。

アウトプットされた値が観測値 \(L_\odot, X_\odot, R_\odot\) に一致するまで、インプットするパラメータ \(X_0, \alpha\) の値を調整しながら計算を繰り返します。一致したときの結果が最終的な標準太陽モデルです。

モデルの実証

日震学 脚注 [日震学]：太陽表面で観測される気体の振動や波を解析することで、太陽内部の圧力や密度、流れの様子などを知ることができます。この手法を日震学と言います。日震学はこれまで、太陽内部の理論モデル (標準太陽モデル) の観測的裏付けを与えた他、太陽内部の自転 (差動回転) の様子も明らかにしました。 と呼ばれる手法を用いることで、標準太陽モデルの精度、つまり実際の太陽内部からの誤差を観測に基づいて推定することができます。詳しくは記事「太陽内部を探る日震学」で説明していますが、大まかには次のような手法です。

太陽表面では、気体が様々な周期で振動している様子が観測されます。この振動は、熱対流などに伴って起こる 音波 脚注 [音波]：プラズマ中も普通の気体と同じように、物質の疎密波 (縦波) が伝わります。これを音波と言います。音波の伝わる速さ (音速) は温度の 1/2 乗に比例するので、注目する場所ごとに異なります。 のような波が太陽内部を伝わった結果、表面が揺らされて起きる現象です。

太陽モデルによって得られた内部の状態から、各場所における音速を計算することができます。すると、それに基づいて、表面で起きる振動の周期も計算することができます。

そうして予測された周期と実際に観測される周期のずれを解析することで、標準太陽モデルが内部の音速をどれだけ間違って見積もっているのかを推定することができます。

この記事で紹介した Christensen-Dalsgaard et al. (1996) のモデルについては、半径 \(0.05R_\odot\) から \(0.95R_\odot\) の範囲では質量密度の誤差が最大で 1.7 % 程度であることが確かめられています。

もう 1 つ、観測的に太陽内部を知る手段として、核融合に伴って生成され、地球に降り注ぐニュートリノの観測があります。詳しくは ニュートリノ問題の記事 で説明していますが、観測されるニュートリノの数は、観測の不確かさの範囲内では大方、標準太陽モデルの予想と一致しています。

組成をどう測るか

太陽表面で各元素がどれくらい存在しているかは、表面から放たれる光を分析することによって、知ることができます。組成を調べる手法を説明するために、まずは我々が見ている太陽の光はどのようにして放射されたものなのかを説明します。詳しくは 黒体放射の記事 でも説明しています。

図 22 に示したように、太陽はある面を境にして、内側が不透明、外側が透明になっています。そしてその境界が太陽表面と呼ばれます。不透明とは、放たれた光が直ぐに吸収されてしまうということです。内部で生成された光は、表面に達することなく吸収されます。

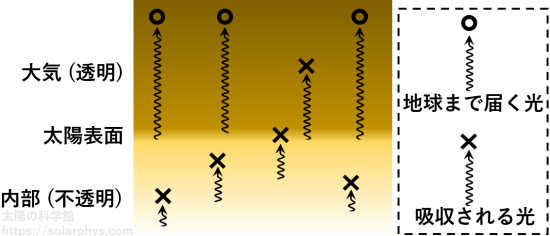
一方、表面で生成された地球向きの光のほとんどは、吸収されることなく地球まで届きます。しかし、一部は表面の外側の太陽大気で吸収されます。

記事「光とは何か？」で説明していますが、光の「色」とは、光を電磁波として考えたときの波長のことです。太陽大気は、表面で発せられた全ての波長の光を吸収するわけではなく、特殊な波長の光のみを吸収します。

詳しくは記事「スペクトル線：なぜ様々な光で観測するのか？」で説明していますが、大気に含まれる各粒子は、粒子の種類ごとに異なった波長の光を吸収します。よって、例えば 図 23 のように、水素原子が吸収する波長の光は大気でたくさん吸収されます。その結果、どの元素にも吸収されない波長の光より強度 (明るさ) が少なくなって地球に届きます。

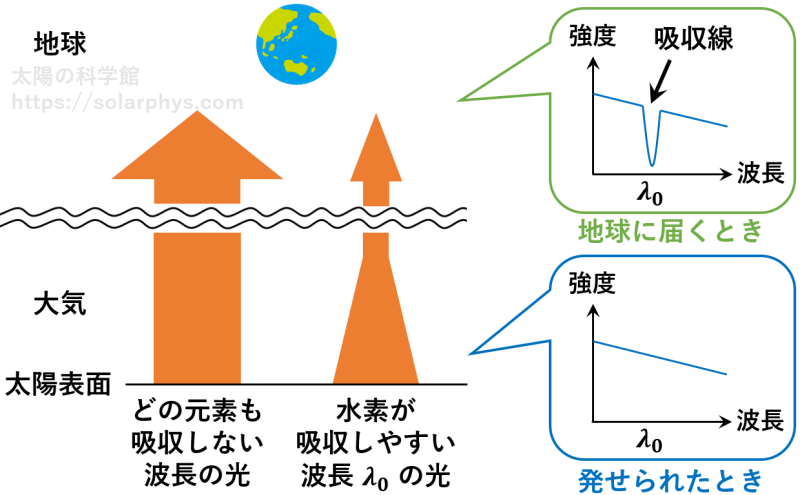
図 23 に示したように、横軸が光の波長、縦軸がその波長の光の強度となるようなグラフ (スペクトル) を描いた場合、地球に届く光は各元素の粒子が吸収する波長だけ凹んだような形になっています。これを吸収線と言います。

例えば 図 24 は、地上で観測された太陽光を波長ごとに分解したものです。色でいうと赤色の波長領域が示されています。縦軸には、どの元素にも吸収されない波長の強度を 1 としたときの相対的な強度が示されています。図にはたくさんの吸収線が映っています。例えば矢印で示した吸収線 (波長 656.3 nm、通称 Hα 線) は太陽大気の水素原子による吸収で形成されています。中には地球の大気で形成される吸収線もあります。

このような吸収線の中から、太陽表面付近での吸収によって形成されるものを選りすぐり、吸収された量を分析することで、その吸収線を作り出す粒子種の存在量を知ることができます。様々な元素の様々な粒子種 (例えば炭素に関係する粒子種なら \(\text{C}\) 原子、\(\text{CH}\)、\(\text{C}_2\)、\(\text{CO}\) など) が作り出す吸収線をひとつひとつ調べていくことで、各元素の含有率を決定します。

ただし、例外として、ヘリウムやネオンなどの希ガス (貴ガス) は、存在量の推定に使いやすい吸収線を作らないため、この方法での推定は難しいです。そのため、他の手法が用いられます。

例えばヘリウムは 日震学 脚注 [日震学]：太陽表面で観測される気体の振動や波を解析することで、太陽内部の圧力や密度、流れの様子などを知ることができます。この手法を日震学と言います。日震学はこれまで、太陽内部の理論モデル (標準太陽モデル) の観測的裏付けを与えた他、太陽内部の自転 (差動回転) の様子も明らかにしました。 を用いて推定されます。日震学を用いると、太陽内部の 音速 脚注 [音波]：プラズマ中も普通の気体と同じように、物質の疎密波 (縦波) が伝わります。これを音波と言います。音波の伝わる速さ (音速) は温度の 1/2 乗に比例するので、注目する場所ごとに異なります。 を推定できると述べました。表面付近では、ヘリウムは部分電離の状態にありますが、これが音速に影響します。よって、表面付近の音速を調べることで、ヘリウムの含有率を精度よく推定することができます。

各元素の具体的な推定方法については、例えば Asplund et al. (2009) にまとまっています。

現在発生している問題

太陽表面での元素の存在比は、吸収線を調べることによって推定されると述べました。この推定は、具体的には次のような手順で行われます。

1. その吸収線を作る粒子の存在比を適当に仮定して、太陽表面付近での光の吸収の様子を 放射輸送理論 脚注 [放射輸送]：太陽を構成するプラズマは高温なので、通常の熱伝導や熱対流に加えて、光を放出したり、近くで放出された光を吸収したりすることによって運ばれるエネルギーも無視することができません。これを放射輸送と言います。周りの物質分布や温度などの情報から、各場所での光の強度を計算するための方程式を放射輸送方程式と言います。 によってシミュレーションし、地球で観測されるはずの吸収線の形を計算する。
2. 計算結果と実際に観測される吸収線の形が合うように、仮定した粒子の存在比を調整しながら計算を繰り返す。
3. 計算結果と観測結果が一致したときの存在比が最終的な推定結果である。

吸収線のシミュレーションを行うためには、太陽表面付近の大気の温度や密度のモデルが必要です。以前は球対称を仮定した太陽大気モデルを用いることで、このシミュレーションを実行していました。そのようなモデルでは、太陽表面での熱対流による効果は簡略化して取り入れられていました。

詳しくは 粒状斑の記事 で説明していますが、近年になって、太陽表面の熱対流を 3 次元的にコンピュータ内で再現できるようになってきました。それを受けて、2000 年以降、そのような 3 次元シミュレーションの結果を吸収線の計算のためのモデルとして採用することで、存在比の推定値の大掛かりな改定が行われました。

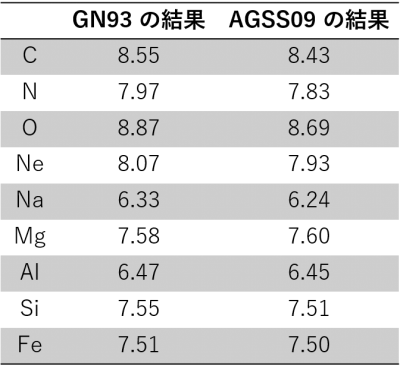
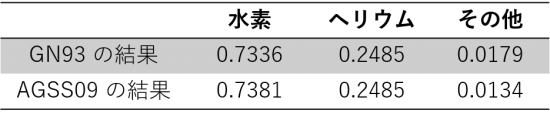
ヘリウムの存在比は上述したように、日震学によって決定されるため、この改定の影響を受けませんが、その他の元素は 表 25 に示したように変更されました。特に、炭素、窒素、酸素をはじめとする元素の存在比は少なくなりました。その結果、 表 26 に示したように、「その他」の元素の質量存在比の推定が小さくなりました。

この「その他」の元素量の改定が現在、標準太陽モデルに関する問題を生んでいます。太陽深部では、水素やヘリウムはほとんど電離しているため、「その他」の元素から成る粒子は、電子を持つ粒子として貴重な存在です。上述したように、電子を持つ粒子の存在は不透明度を大きくするため、「その他」の元素の存在比は太陽内部の不透明度の値に大きく影響します。

この記事で紹介した Christensen-Dalsgaard et al. (1996) の標準太陽モデル (Model S) は、Grevesse & Noels (1993) ( 表 26 の上 ) のデータを用いて計算されたものです。このモデルの実際の太陽内部からの誤差は、すでに述べたように、質量密度にして 1.7 % 程度です。しかし、Asplund et al. (2009) ( 表 26 の下 ) の新しいデータを用いて計算された標準太陽モデルは、その誤差が質量密度にして 4 % 程度 ( Turck-Chièze, 2016 ) と、Model S よりも大きくなってしまいます。

両モデルの食い違いは対流層の深さにも表れます。日震学によって推定された実際の太陽の放射層と対流層の境界は、半径 \((0.713\pm 0.001) R_\odot\) の位置にあります ( Basu & Antia, 1997 )。Model S の値は \(0.712R_\odot\) であるのに対し、Asplund et al. (2009) の結果を用いた標準太陽モデルでは、\(0.724R_\odot\) となります ( Christensen-Dalsgaard, 2020 )。

元素の存在比の改定結果が間違っているのか？それとも改定結果は正しく、標準太陽モデルの方を改良すべきなのか？だとしたらなぜ Model S はより正しい結果を与えているのか？様々な研究が行われていますが、まだ有力な説は存在しないようです。

参考文献

記事全体として参考にしたレビュー (書籍)

• Christensen-Dalsgaard, J. (2021). Solar structure and evolution. Living Reviews in Solar Physics, 18, 2 .
• Kippenhahn, R., Weigert, A. and Weiss, A. (2012). Stellar Structure and Evolution, 2nd edn. (Berlin: Springer ).

引用した文献

• Asplund, M., Grevesse, N., Sauval, A. J. and Scott, P. (2009). The chemical composition of the Sun. Annual Review of Astronomy and Astrophysics, 47, 481-522 .
• Basu, S. and Antia, H. M. (1997). Seismic measurement of the depth of the solar convection zone. Monthly Notices of the Royal Astronomical Society, 287, 189-198 .
• Basu, S. and Antia, H. M. (2004). Constraining solar abundances using helioseismology. The Astrophysical Journal Letters, 606, L85-L88 .
• Christensen-Dalsgaard, J., Däppen, W., Ajukov, S. V., Anderson, E. R., Antia, H. M., Basu, S., Baturin, V. A., Berthomieu, G., Chaboyer, B., Chitre, S. M., Cox, A. N., Demarque, P., Donatowicz, J., Dziembowski, W. A., Gabriel, M., Gough, D. O., Guenther, D. B., Guzik, J. A., Harvey, J. W., Hill, F., Houdek, G., Iglesias, C. A., Kosovichev, A. G., Leibacher, J. W., Morel, P., Proffitt, C. R., Provost, J., Reiter, J., Rhodes Jr., E. J., Rogers, F. J., Roxburgh, I. W., Thompson, M. J. and Ulrich, R. K. (1996). The current state of solar modeling. Science, 272, 1286-1292 .
• Fröhlich, C. and Lean, J. (2004). Solar radiative output and its variability: evidence and mechanisms. The Astronomy and Astrophysics Review, 12, 273–320 .
• Gabriel, A. H. (1976). A magnetic model of the solar transition region. Philosophical Transactions of the Royal Society A, 281, 339-352 .
• Golding, T. P., Leenaarts, J. and Carlsson, M. (2016). Non-equilibrium helium ionization in an MHD simulation of the solar atmosphere. The Astrophysical Journal, 817, 125 .
• Grevesse, N. and Noels, A. (1993). In Origin and Evolution of the Elements, ed. N. Prantzos, E. Vangioni-Flam and M. Cassé, pp. 15-25 (Cambridge: Cambridge University Press).
• Grevesse, N. and Sauval, A. J. (1998). Standard solar composition. Space Science Reviews, 85, 161–174 .
• Leenaarts, J., Carlsson, M., Hansteen, V. and Rutten, R. J. (2007). Non-equilibrium hydrogen ionization in 2D simulations of the solar atmosphere. Astronomy & Astrophysics, 473, 625-632 .
• Turck-Chièze, S. (2016). The standard solar model and beyond. Journal of Physics: Conference Series, 665, 012078 .
• Vernazza, J. E., Avrett, E. H. and Loeser, R. (1981). Structure of the solar chromosphere. III. Models of the EUV brightness components of the quiet Sun. The Astrophysical Journal Supplement Series, 45, 635-725 .