太陽の自転

図 1 は観測衛星 SDO が捉えた太陽表面 (
光球
脚注
[光球]:フィルターを通さずに可視光で観測したときに明るく映る層のことです。大雑把にはこの層が「太陽表面」と呼ばれます。より細かくは高度 0 から 500 km あたりの層を言います。
 ) とその上空の
コロナ
脚注
[コロナ]:高度数千 km より高層の大気を指します (太陽半径は約 70 万 km)。極端紫外線や X 線で見ることができます。
) とその上空の
コロナ
脚注
[コロナ]:高度数千 km より高層の大気を指します (太陽半径は約 70 万 km)。極端紫外線や X 線で見ることができます。
 の映像です (
図の色について
脚注
[図の色]:図に映っている太陽の色は人工的に着けられたものです。惑わされないでください。これらの図は、特定の波長の光だけを通すフィルターを付けた望遠鏡によって撮影されたものであり、要はモノクロ画像です。得られた光の強度を慣習に従った色によって図示しています。
)。現実の 66 時間分の様子が映っています。図を見ると、光球の黒点やコロナの明るい部分のような構造が徐々に右に移動していきます。これは太陽が回転しているからです。太陽は大体 30 日で一回りの周期で自転しています。我々は太陽面 (球面) のうちの地球側の半分のみを見ることができるわけですが、その見える面も自転に伴って移り変わっていきます。
の映像です (
図の色について
脚注
[図の色]:図に映っている太陽の色は人工的に着けられたものです。惑わされないでください。これらの図は、特定の波長の光だけを通すフィルターを付けた望遠鏡によって撮影されたものであり、要はモノクロ画像です。得られた光の強度を慣習に従った色によって図示しています。
)。現実の 66 時間分の様子が映っています。図を見ると、光球の黒点やコロナの明るい部分のような構造が徐々に右に移動していきます。これは太陽が回転しているからです。太陽は大体 30 日で一回りの周期で自転しています。我々は太陽面 (球面) のうちの地球側の半分のみを見ることができるわけですが、その見える面も自転に伴って移り変わっていきます。
表面では様々な緯度に黒点が見られますが、それらの自転に伴う動きを細かく追うと、太陽は高緯度より低緯度の (赤道に近い) 方が速く自転していることが分かります。「差動回転 (differential rotation)」と呼ばれる現象です。例えば地球は基本的に岩石でできた固体なので、全体として同じ角速度で自転しますが、太陽は主に水素とヘリウムから成る気体なので、そのような回転の仕方が可能です。
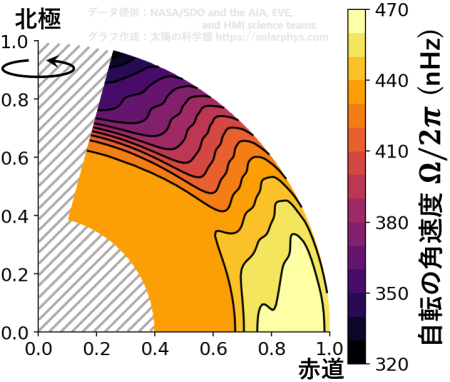
更に、 日震学 脚注 [日震学]:太陽表面で観測される気体の振動や波を解析することで、太陽内部の圧力や密度、流れの様子などを知ることができます。この手法を日震学と言います。日震学はこれまで、太陽内部の理論モデル (標準太陽モデル) の観測的裏付けを与えた他、太陽内部の自転 (差動回転) の様子も明らかにしました。 とよばれる手法を用いることによって、太陽表面だけでなく、内部の自転の様子まで詳しく分かっています。図 2 はその結果です。図の読み方はキャプションを読んでください。中心付近や極付近の推定には不確かさが伴うので、図では除外しました。
日震学について詳しくは記事「太陽内部を探る日震学」で説明していますが、大雑把に説明すると、地震学と同じような手法です。地震が起きると地表が揺れます。各地の揺れ方から地震波が地中を伝わる様子を推定することによって、地中の構造 (密度や温度など) を知ることができます。太陽表面でも振動が観測されます。その振動の様子を調べることによって、内部の情報を得ることができます。
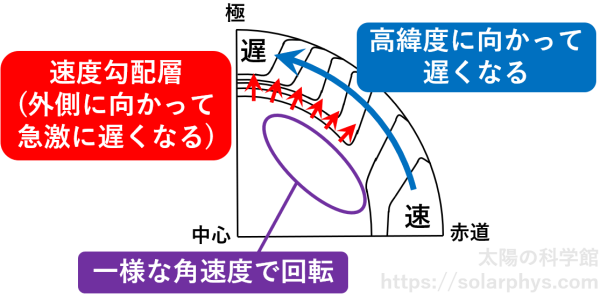
図 2 を見ると、赤道は大体 25 日で一周という速い周期で自転しており、自転速度は高緯度に行くほど遅くなります。極付近の周期は 35 日程度です。そのような構造は表面から半径 \(0.7 R_\odot\) 程度の領域まで続いています。\(R_\odot\) は太陽半径です。一方で、半径 \(0.7 R_\odot\) より深い (中心に近い) 領域では自転速度の差はほとんどなく、ほぼ一様の角速度で回転していることが分かります ( 図 3 の紫 )。両者の間には自転速度が急激に変化する「速度勾配層 (タコクライン、tachocline)」と呼ばれる領域が存在します ( 図 3 の赤 )。
記事「11 年周期:太陽の睡眠サイクル」で説明していますが、差動回転や下で説明する子午面環流、熱対流は太陽の磁場の生成・維持にとって重要な役割を果たしていると考えられています。太陽内部の流れを理解することは、黒点や 11 年周期に代表される磁気活動の理解のためにも重要です。
回り方がおかしい?
太陽の自転の起源については、太陽誕生の時まで遡ります。46 億年前、宇宙のとある場所に散らばっていたガスの中の、特に濃い部分が重力によって収縮することで太陽が生まれました ( 図 4 )。

物質が収縮すると、排水溝に落ち込む水のように回転を始めます。形成された原始太陽はしばらくの間、更に収縮を続け、中心部の圧力を上げていきます。回転するフィギュアスケーターが手足をギュッと縮めると、回転が速まります。この要領で、原始太陽はどんどん角速度を得ていきます。このことをもう少し物理的に説明すると次の通りです。
\begin{align} \mathcal{L}&= \lambda \times v \\ &= \lambda^2 \times \Omega\\ \text{ただし},&\quad \lambda: \text{回転軸からの距離} \ [\text{m}] \\ &\quad v: \text{回転の速さ} \ [\text{m s}^{-1}]\\ &\quad \Omega: \text{回転の角速度} \ [\text{rad s}^{-1}] \end{align}
回転している物質中の特定の部分に注目したとき、その物質の速さ \(v\) と回転軸からの距離 \(\lambda\) に対して上式で計算される量 \(\mathcal{L}\) を、その物質が単位質量あたりに持つ角運動量と言います。この \(\mathcal{L}\) は、他の物質との間で特に何らかのやり取りが行われない限り、増えることも減ることもありません。太陽に向かって物質が落ち込むと上式の \(\lambda\) が小さくなるので、\(\mathcal{L}\) を保存するために、代わりに \(v\) \((\Omega)\) が大きくなります。つまり、その物質が太陽中心に近づくほど回転が速まるわけです。
やがて、中心部の圧力が十分になったところで核融合反応が始まり、収縮は止まります。これが太陽の誕生です。完全に収縮できずに太陽の周りに取り残された物質は、それぞれの場所で塊に成長し、惑星となります。この取り残された物質も太陽と同じ方向に回転しているわけですので、形成された惑星も太陽の自転と同じ方向に公転することになります。この意味で、太陽自転と惑星公転の起源は同じと言えます。
誕生当時の太陽の自転速度は現在より速かったと考えられています。どの程度速かったかを推定することは難しいのですが、太陽に似た質量を持つ若い星たちの観測から類推するに、現在の数倍だったかもしれないし、はたまた数十倍だったかもしれないというスケールの話です ( Gallet & Bouvier, 2013 )。
記事「太陽風:常に噴き出すスプリンクラー」で詳しく説明していますが、太陽は常に表面から宇宙空間に向かって物質をまき散らしています。「太陽風」と呼ばれる現象です。この太陽風が太陽の持つ角運動量の内のいくらかを持ち去っていくので、その分だけ自転は常に減速しています。この減速は微々たるものなので、100 年や 1000 年そこらで劇的に角速度が落ちるわけではないのですが、それでも誕生から 46 億年という長い時が経てば、かなり減速します。その結果、現在の自転周期は大体 1 ヶ月になっています。
このシナリオに従って素朴に考えれば、自転は表面から徐々に減速していくので、現在は中心が速く、表面が遅いような自転構造になっていても良いような気がします。あるいは角運動量保存則に従うなら、自転軸に近いほど速く回っているような構造も想像できます。しかし、実際の太陽は上述したような差動回転をしています。差動回転を維持する確固たる機構が存在するはずです。
この謎についての現在の理解は、大雑把に「こうなんじゃないか?」という候補は存在するけれども、具体的な話をすると分からないことが多い、という状況に見受けられます。キーワードは「乱流」です。この「乱流」をどう理解するかという問題は、太陽に限らず、 流体力学 脚注 [流体力学]:液体や十分に濃い気体の速度、温度、圧力や密度などの時間発展を計算するための理論を流体力学と言います。 を扱う様々な分野が現在直面しています。
太陽表面の熱対流
太陽内部には差動回転の他にも、大きく分類して 2 種類の流れが存在することが分かっています。「
熱対流
脚注
[熱対流]:水の入った鍋を下からコンロで熱すると、熱くなった底付近の水は軽くなって上方へ移動します。逆に元々鍋の上方にあった水は熱せられた水と比べて重いため、下方へ移動します。これの繰り返しによって、鍋の中の水は温度を一様にしようとします。これが熱対流です。エネルギーの観点では、下からコンロによって加えられる熱エネルギーを熱対流が上方へ輸送していることになります。
 (thermal convection) 」と「子午面環流 (meridional circulation)」 です。この節ではまず、太陽表面で観測される熱対流について説明します。
(thermal convection) 」と「子午面環流 (meridional circulation)」 です。この節ではまず、太陽表面で観測される熱対流について説明します。
記事「粒状斑:太陽表面での対流」で説明しているように、太陽表面での熱対流は味噌汁で見られる模様のような粒状斑 (granulation) として観測されます ( 図 5 参照 )。
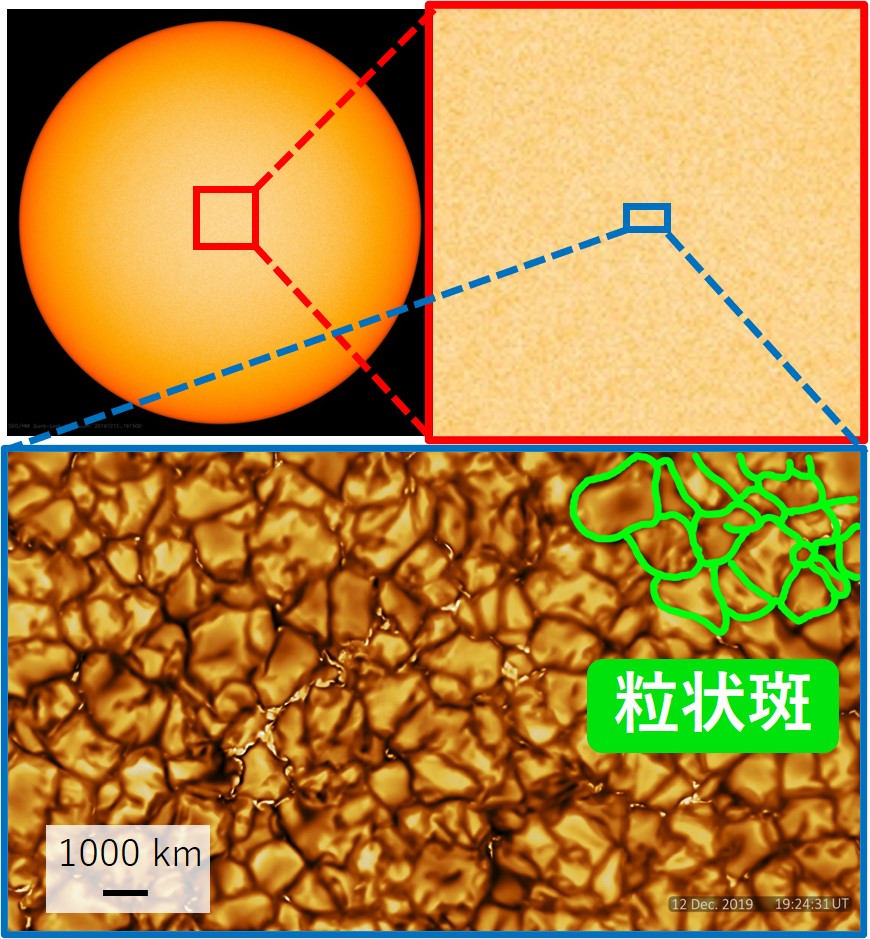
太陽は基本的に深いほど温度が高くなっています。図 6 に模式図を示しましたが、内部から表面に大体 1 万 \(\text{K}\) ( ケルビン 脚注 [ケルビン]:温度の単位には基本的にケルビン (K) を用います。日常で使われる摂氏と目盛の幅は同じであり,摂氏 0 度は 273.15 K です。つまり,例えば 300 K は摂氏 26.85 度のことです。 ) の熱い気体が上昇してきます。上昇してきたばかりの比較的熱い気体が図 5 では明るく映っています。表面では常にエネルギーが光として宇宙空間に逃げて行くので、上昇してきた気体は大体 6000 \(\text{K}\) まで冷やされます。すると、明るさを失うと同時に周囲より重くなるため、今度は下降流に転じます。これが 図 5 では対流セル (細胞状の構造) とセルの間の暗い線として見えています。

粒状斑 (表面での対流) の大きさは典型的には \(1000 \ \text{km}\) 程度です。これは大体日本の本州くらいの大きさです。気体の流速は \(1 \ \text{km s}^{-1}\) 程度であることが分かっています。参考として、太陽半径は 約 70 万 \(\text{km}\) です。粒状斑について詳しくは例えば Nordlund et al. (2009) を読んでください。
図 7 は米国の国立天文台 (NSO) が YouTube に上げている動画です。ハワイにある望遠鏡 DKIST が捉えた粒状斑の様子が映っています。一つ一つの対流セルの形は数分のスケールでどんどん変化していき、他のセルに飲み込まれたり、はたまた分裂したりと、混沌とした様相です。このように、一見すると無秩序で、様々な大きさの流れが混在するような状態を「乱流 (turbulence)」と言います。
太陽表面には粒状斑の 1000 \(\text{km}\) スケールでの熱対流に加え、3 万 \(\text{km}\) スケールの対流が存在することも知られています。「超粒状斑 (supergranulation)」と呼ばれる現象です。 図 8 にその様子を示します。

詳しくは記事「プラズマ診断:太陽を「見る」だけでここまで分かる」で説明していますが、観測される光を分析することで、太陽表面の気体の視線速度を知ることができます。視線速度とは、気体が観測衛星から遠ざかる向きに速度を持つか、近づく向きに速度を持つかということです。 図 8 は得られた太陽面全体に渡る視線速度の様子から、差動回転や後に述べる子午面環流による寄与を取り除いたものです。図の読み方はキャプションを見てください。
図を見ると、ブツブツ模様が見えます。各ブツブツの大きさは典型的には 3 万 \(\text{km}\) 程度です。他にも複数の種類の観測から、このスケールの流れが存在することが分かっています。このように、太陽表面は 2 つのスケールの流れを主要素とした乱流状態にあります ( 図 9 )。

粒状斑の記事 でも説明していますが、2 つの対流要素の内、粒状斑対流は素朴な熱対流理論とも合致し、コンピュータシミュレーションによって上手く再現されています。しかし、超粒状斑の方は、まだその起源がよく分かっていません。太陽内部の熱対流の一片が表面に表れているものであろうと考えられますが、超粒状斑の特徴を十分に説明できる理論は今のところありません ( 詳しくは例えば Rincon & Rieutord, 2018 )。
以上、太陽表面が熱対流による乱流状態にあることが観測から明らかになっていると説明しました。この熱対流は太陽内部にも存在していて、半径 0.7 \(R_\odot\) (\(R_\odot\) は太陽半径) の領域まで続いていると考えられています。記事「基本構造:何からできているのか?」で説明している
対流層
脚注
[対流層]:太陽半径を \(R_\odot =\) 約 70 万 km としたとき、\(0.7 R_\odot \)から表面 (\(1 R_\odot\)) までの領域を指します。この領域では主に熱対流によってエネルギーが外側へと運ばれます。
 のことです。
のことです。
対流層内部での熱対流は太陽表面よりも大きく、ゆっくりであると考えられています。典型的な大きさは大雑把に 1 - 10 万 \(\text{km}\) の桁数、流速は 10 - 100 \(\text{m s}^{-1}\) の桁数と思われますが、この記事の下の方で述べるように、細かいことはよく分かっていません。
見えにくい子午面環流
太陽内部の流れを大きく 3 種類に分けたとき、 1 つ目は差動回転、 2 つ目は熱対流でした。残る 1 つは子午面環流と呼ばれる流れです。上で対流層内部は熱対流による乱流状態にあると述べました。その乱流の複雑な動きを
経度方向
脚注
[極座標]:半径 \(r\)、余緯度 \(\theta\)、方位角 \(\phi\) の 3 つの値で点を指定する方法を極座標 (球座標) と言います。太陽は大雑把に球対称の天体なので、極座標がよく用いられます。方位角は経度とも言います。余緯度は北極から測った角度ですが、代わりに赤道から測った角度である緯度が用いられることもあります。球を縦に (北極と南極を通るように) 切った平面を子午面と言います。
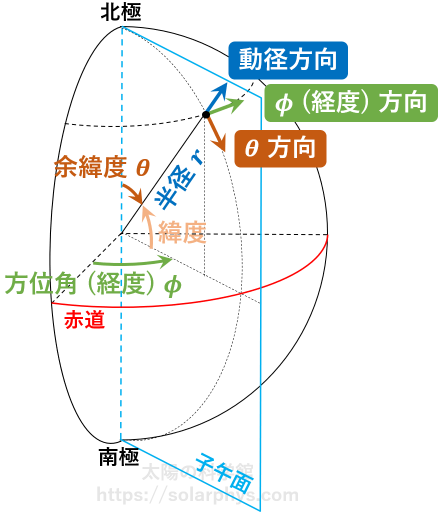 一周に渡って平均し、更に何年にもわたって時間でも平均すると、浮き彫りになった
子午面
脚注
[極座標]:半径 \(r\)、余緯度 \(\theta\)、方位角 \(\phi\) の 3 つの値で点を指定する方法を極座標 (球座標) と言います。太陽は大雑把に球対称の天体なので、極座標がよく用いられます。方位角は経度とも言います。余緯度は北極から測った角度ですが、代わりに赤道から測った角度である緯度が用いられることもあります。球を縦に (北極と南極を通るように) 切った平面を子午面と言います。
一周に渡って平均し、更に何年にもわたって時間でも平均すると、浮き彫りになった
子午面
脚注
[極座標]:半径 \(r\)、余緯度 \(\theta\)、方位角 \(\phi\) の 3 つの値で点を指定する方法を極座標 (球座標) と言います。太陽は大雑把に球対称の天体なので、極座標がよく用いられます。方位角は経度とも言います。余緯度は北極から測った角度ですが、代わりに赤道から測った角度である緯度が用いられることもあります。球を縦に (北極と南極を通るように) 切った平面を子午面と言います。
 内の流れはあるパターンを描くのではないかと考えられています。
内の流れはあるパターンを描くのではないかと考えられています。
子午面環流の推定結果の一例を 図 10 に示します。図では、子午面環流の流れ方を表す線 (流線) が表されています。色は流速の
\(\theta\) 方向
脚注
[極座標]:半径 \(r\)、余緯度 \(\theta\)、方位角 \(\phi\) の 3 つの値で点を指定する方法を極座標 (球座標) と言います。太陽は大雑把に球対称の天体なので、極座標がよく用いられます。方位角は経度とも言います。余緯度は北極から測った角度ですが、代わりに赤道から測った角度である緯度が用いられることもあります。球を縦に (北極と南極を通るように) 切った平面を子午面と言います。
 成分の大きさです。Gizon et al. (2020) の推定結果によると、例えば緯度 30 度に注目したとき、太陽表面 (\(R_\odot\)) では \(10 \ \text{m s}^{-1}\) 程度の極向きの流れ、半径 \(0.72 R_\odot\) では数 \(\text{m s}^{-1}\) 程度の赤道向きの流れが存在します。
成分の大きさです。Gizon et al. (2020) の推定結果によると、例えば緯度 30 度に注目したとき、太陽表面 (\(R_\odot\)) では \(10 \ \text{m s}^{-1}\) 程度の極向きの流れ、半径 \(0.72 R_\odot\) では数 \(\text{m s}^{-1}\) 程度の赤道向きの流れが存在します。
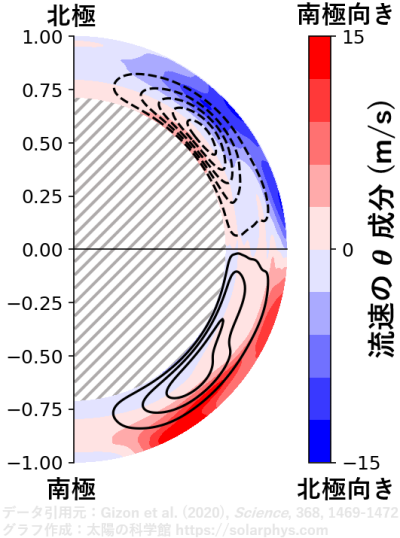
子午面環流の推定も日震学によってなされますが、差動回転とは異なり、用いる観測データや推定方法に結果が大きく依存してしまいます。しかも、なぜ異なる結果が導かれるのか、未だに原因特定に至っていないのが現状です。詳しくは日震学の記事で説明します。
図 10 の研究 ( Gizon et al., 2020 ) では、異なる 3 つの観測装置によって得られたデータを用意して同じ解析を行ったところ、2 つのデータにおいて同じ結果が得られたために、その結果が示されています。しかし、残りの 1 データを用いた解析では異なる結果が得られ、その原因は特定できていないと報告されています。

Gizon et al. (2020) の結果では北半球と南半球に 1 つずつ、大きな環流が存在していますが、図 11 のように複数の環流に分かれていることを示唆するような研究結果も存在します。表面で極向きの流れがあることは確かですが、対流層の奥深くの流れの推定には大きな不確かさがあります。他の研究結果について詳しくは、例えば Mandal et al. (2018) の Introduction を読んでください。
日震学を用いて推定される子午面流は、何年にも渡って平均したときの構造です。より短い、例えば 1 ヶ月で平均したときの構造を推定することは、現在の技術ではできません。最近のシミュレーションの結果からは、子午面流は数週間のような短い時間スケールでは頻繁に構造を変えているのではないかと考えられるようになってきましたが、そのことを観測で実証できるようになるにはまだ時間がかかるかもしれません。
太陽内部の対流のイメージ
差動回転の駆動源は熱対流にあると考えられています。それも、上述した太陽表面での熱対流ではなく、対流層内部での熱対流です。内部の対流の様子を、例えば日震学のような手法で観測から推定することはまだ難しいです。この節ではコンピュータシミュレーションの結果を示すことで、対流構造の大雑把なイメージをつかんでいただくことを目標にします。ただし、下の節で述べるように、シミュレーションが実際の太陽内部をどれほど再現できているのかについては、まだ多くの疑問が残っています。
図 12 は太陽や恒星内部の流れの様子を調べるためのシミュレーション結果の例です。対流層に見立てた球殻状の箱をコンピュータ上に作り、流体力学の方程式を計算しています。内側から熱を与え、箱を様々な速さで回転させて、起こる対流の様子を調べます。(a) は箱を速く回転させたとき、(b) はゆっくり回転させたときの典型的な結果を表します。
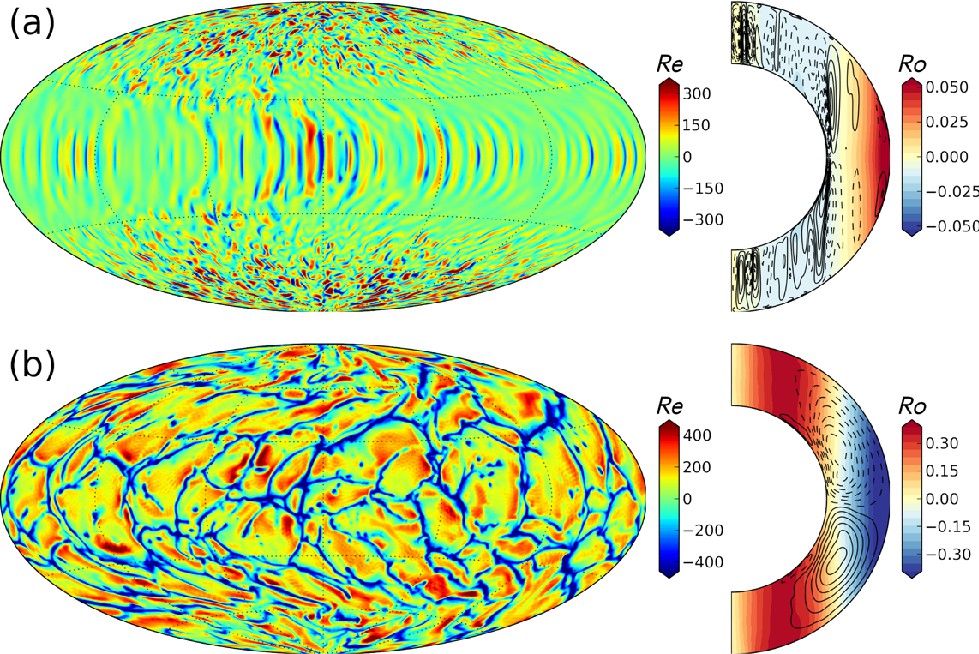
今は図の左側に注目してください。ある瞬間の表面近くでの流れの様子が示されています。赤色は上昇流 (外向きの流れ) がある領域、青色は下降流 (内向きの流れ) がある領域です。速く回転させた場合とゆっくり回転させた場合では、かなり対流の様子が違っていることが分かります。ゆっくり回転させた場合 (b) は、大きな細胞状の対流が見えます。一方で、速く回転させた場合 (a) は、低緯度に縦向きの細長い構造が並んでいます。この対流構造は見かけの通り、「バナナセル」と呼ばれたりします。
このように、系が違う状況下にあると、対流の構造・特徴も変化します。これは言い換えると、乱流の統計的性質が変化するということです。太陽は図の (a) と (b) の中間的な状態にあると考えられています。上述した表面での熱対流にバナナセルような構造は見られませんが、対流層の内部ではバナナセルが存在しているかもしれません。
太陽内部の対流に対するイメージをつかんでいただくために、次の動画も紹介します。図 13 は『天文学普及プロジェクト 天プラ』という団体が YouTube に上げている動画です。Hotta et al. (2015) の研究の紹介動画です。動画では、対流層内部の流れを再現するシミュレーションの結果が説明されています。

これらのシミュレーション結果が示すように、対流層内部には表面よりも大きなスケールの熱対流が起きていると考えられています。表面の粒状斑は既に述べたように、5 分や 10 分で様子が変化していきます。この時間スケールは自転周期 30 日よりもずっと短いため、粒状斑は自転の影響を受けません。
表面はエネルギーが光として逃げて行くことで強く冷やされています。この影響もあって、粒状斑は激しい対流状態にあります。これは対流層全体の中では例外的な状況です。内部の対流はもっと自転周期に近い時間スケールを持つと考えられています。このため、自転の影響 ( =
コリオリの力
脚注
[コリオリの力]:地球や太陽のような回転 (自転) する系の中で物質が速度を持つと受ける見かけの上の力 (慣性力) のことを言います。地球の外 (慣性系) から見ると等速直線運動をしている物体でも、回転する地球に固定された観測者 (回転系) からは軌道が曲がって見えます。これは回転系で考える場合には、「遠心力」「コリオリの力」の 2 つの慣性力を物体が受けていると解釈すれば辻褄が合います。遠心力は物体の運動に依らず外向きに働く力であり、コリオリの力は物体が回転系で見て動いている場合に遠心力に加えて働く力です。自転軸に沿って南極から北極を見た向きを \(\vec{\Omega}\)、回転系で見た物体の速度を \(\vec{v}\) としたとき、コリオリの力は外積 \(\vec{v}\times\vec{\Omega}\) の向きに働きます。
 ) を受けて特殊な統計的性質を持ちます。
) を受けて特殊な統計的性質を持ちます。
その統計的性質が差動回転を駆動していると考えられていますが、対流 (乱流) が具体的にどのような性質を持つのかを解明することは、非常に難しい問題です。
対流層の乱流は、流体力学的には「非常に激しい状態」に位置付けられるため、方程式を手で解いて (解析的に) 調べることは難しいです。対流層は下部の質量密度が上部の 100 倍と、激しい 重力成層 脚注 [重力成層]:下向きに重力がかかっているところに気体が積み重なると、下の気体は上に乗っている気体に押しつぶされて密度や圧力が高くなります。このように、上に行くほど密度や圧力が低くなるように気体が積み重なった状態を重力成層と言います。地球の大気も重力成層しているため、高い山に登ると空気が薄くなります。 下にあります。また、構成する気体は非常にサラサラの (粘度の低い) 状態です。そのような環境を実験室で再現するのも難しい挑戦です。
従って白羽の矢が立つのが、上で示したようなコンピュータシミュレーションです。しかし、乱流が太陽全体に及ぼす影響を調べるためには、太陽全体のスケールと細かい乱流のスケールを同時に計算しなければなりません。そのためには速い計算速度が必要です。シミュレーション研究の発展を担う大きな要因はスーパーコンピュータの計算速度の向上です。
現在のシミュレーションでは、とりあえず対流層内部の熱対流の典型的なスケールを解像することはできていますが、下で述べるように、まだ問題も多く残っています。もっと精度が上がれば、まだ見ぬ現象が見えてくるだろうと期待されています。
無秩序が秩序を生む?
赤道が速く回る差動回転の構造は、熱対流の統計的性質が決めていると考えられています。乱流状態にある熱対流の細かな動きの一つ一つは、一見すると無秩序でも、それらの動きを平均的に見ると、赤道方向に自転の角運動量を運ぶ役割を果たしています。そのような効果が積もり積もって太陽全体に差動回転の流れ構造をもたらすのです。このことをもう少し丁寧に説明します。

対流層の乱流を
極座標
脚注
[極座標]:半径 \(r\)、余緯度 \(\theta\)、方位角 \(\phi\) の 3 つの値で点を指定する方法を極座標 (球座標) と言います。太陽は大雑把に球対称の天体なので、極座標がよく用いられます。方位角は経度とも言います。余緯度は北極から測った角度ですが、代わりに赤道から測った角度である緯度が用いられることもあります。球を縦に (北極と南極を通るように) 切った平面を子午面と言います。
 で考えることにします。つまり、流速を \(v_r,v_\theta,v_\phi\) の 3 つの成分に分けて考えます ( 図 14 )。\(v_r\) は動径方向 (鉛直上向き、外向き) の成分で、\(v_\theta\) は南向きの水平成分、\(v_\phi\) は経度が増える方 (地球でいう東) を向いた水平成分です。
で考えることにします。つまり、流速を \(v_r,v_\theta,v_\phi\) の 3 つの成分に分けて考えます ( 図 14 )。\(v_r\) は動径方向 (鉛直上向き、外向き) の成分で、\(v_\theta\) は南向きの水平成分、\(v_\phi\) は経度が増える方 (地球でいう東) を向いた水平成分です。
対流層内のある場所に注目します。乱流状態にあるため、その場所での流速は時々刻々と乱雑に変化しているでしょう。ある瞬間の流速の \(\theta\) 成分と \(\phi\) 成分が例えば \((v_\theta,v_\phi) = (2,1)\) という値だったならば、図 15 の左のグラフように点を書き込みます。次の時刻の流速が \((v_\theta,v_\phi) = (0.5,-1)\) という値だったなら、またグラフに点を書き加えます。これを繰り返していくと、初めは乱雑な運動をしているように見えても、グラフに書き込まれた点が増えると共に何らかの傾向が見えてくるかもしれません。

仮に 図 15 の右のような正の相関が表れたとします。この相関は「\(v_\phi\) が正 (負) の値を持つとき、その場所での \(v_\theta\) の値は正 (負) になりがちである」ということを言っています。\(v_\phi\) が正とは、注目している場所がその時刻により速く自転している ( = より大きな角運動量を持っている ) ということです。北半球全体に渡ってこの相関が見られた場合、「より大きな (小さな) 角運動量を持つ物質は \(v_\theta \gt 0\) の向き (\(v_\theta \lt 0\) の向き) に移動しがち」という傾向が存在することになります。これは正味として、角運動量が赤道向きに輸送されることを意味します。
このように、不規則に見える乱流の動きが統計的に何らかの傾向を持つと、乱流の存在によって角運動量が運ばれることになります。従って、太陽内部の乱流がどのような相関を持っているのかを調べることが、差動回転の起源を知るための重要な課題です。
上述したような相関は
コリオリの力
脚注
[コリオリの力]:地球や太陽のような回転 (自転) する系の中で物質が速度を持つと受ける見かけの上の力 (慣性力) のことを言います。地球の外 (慣性系) から見ると等速直線運動をしている物体でも、回転する地球に固定された観測者 (回転系) からは軌道が曲がって見えます。これは回転系で考える場合には、「遠心力」「コリオリの力」の 2 つの慣性力を物体が受けていると解釈すれば辻褄が合います。遠心力は物体の運動に依らず外向きに働く力であり、コリオリの力は物体が回転系で見て動いている場合に遠心力に加えて働く力です。自転軸に沿って南極から北極を見た向きを \(\vec{\Omega}\)、回転系で見た物体の速度を \(\vec{v}\) としたとき、コリオリの力は外積 \(\vec{v}\times\vec{\Omega}\) の向きに働きます。
 の影響によって生まれると考えられています。実際の太陽で具体的にコリオリの力がどう機能しているのかは、まだ分からないことも多いですが、例えば次の可能性が挙げられます。
の影響によって生まれると考えられています。実際の太陽で具体的にコリオリの力がどう機能しているのかは、まだ分からないことも多いですが、例えば次の可能性が挙げられます。

仮に対流層内部にバナナセル構造が存在する場合、 図 16 (A) のように、縦向きに並んだ下降流存在域に向かう \(\phi\) 方向の流れが卓越することが予想されます。この水平流には 図 16 (B) のように、北半球と南半球で反対向きのコリオリの力が働きます。それによって、流れの方向が曲げられ、\(v_\phi\) と \(v_\theta\) の間に北半球で正、南半球で負の相関が表れることが期待されます。もしそのような相関が実現すれば、角運動量は赤道向きに運ばれ、赤道が極に比べて加速されることになります。
シミュレーションが抱える問題
差動回転の研究では、大まかに「平均場モデル」「全球シミュレーション」の 2 種類の手法が用いられてきました。このうち、平均場モデルでは問題を次の 2 つに分けます。
- 対流層内の各緯度、半径での乱流は、コリオリの力の影響で、それぞれどのような向きにどれくらいの熱や角運動量を運びうるのか?
- 太陽のような差動回転を実現するためには、どのような熱輸送・角運動量輸送のパターンが要求されるのか?
1 の研究は、単純化した方程式を手で (解析的に) 解いたり、対流層の一部を模した箱の中で局所的な乱流のシミュレーションを行うことでなされました。そうして求まった乱流の性質が、太陽のような差動回転を生むことができるのかが 2 の研究で調べられました。
この平均場モデルは一定の成功を収め、差動回転の理論の大枠が作られましたが、用いられているのは幾分か単純化したモデルであるため、それが実際の太陽でちゃんと働いているかどうかについては疑問が残ります。
2000 年代後半からは、コンピュータの計算能力の向上に伴って、上の節で結果を示したような全球シミュレーションを行う研究グループが増えました。これは、対流層を模した球殻状の箱で、なるべく単純化を施さずに方程式を解くことにより、乱流から差動回転までをひとりでに再現させようという試みです。
こちらの手法だと、例えばバナナセルのような、対流層が球殻状だからこそ起きる現象も考慮に入れることができるため、より現実的な太陽内部の再現ができると期待されています。しかし、現在のところでは、まだ忠実に再現できているとは言えない状況のようです。全球シミュレーションが直面する問題をいくつか紹介します。
熱対流の強さを過大評価している?
図 17 に 図 12 を再掲します。今度は図の右側にも注目してください。速い回転 (a) と遅い回転 (b) のそれぞれの場合について、計算結果を平均して得られた差動回転の構造が色で示されています。赤色は速く、青色は遅く自転している領域を表します。

(a) では実際の太陽と同じように、赤道が速く回っています。対して (b) では極の方が速く回っています。このように、
(a) 回転が速いと赤道が加速 (with バナナセル)
(b) 回転が遅いと極が加速
のパターンは全球シミュレーション結果で広く見られる性質です。(a) では、乱流による角運動量輸送が上手く働いているため、赤道が加速されています。(b) では、乱流へのコリオリの力の影響が弱く、角運動量を輸送する効率が小さいために、子午面環流にかき混ぜられて角運動量が一様に近づく効果の方が勝ってしまい、回転軸に近いほど速く回る構造になっていると考えられます。
計算結果が (a) になるか (b) になるかを分かつのは、コリオリの力が熱対流に与える影響力の強さです。その指標として、次のロスビー数 \(Ro\) というものが用いられます。
\begin{align} & \qquad Ro = \frac{V}{2\Omega L} \\ \text{ただし},&\quad V: \text{対流の典型的な流速} \ [\text{m s}^{-1}] \\ &\quad \Omega: \text{自転の平均角速度} \ [\text{rad s}^{-1}] \\ &\quad L: \text{対流の典型的な大きさ} \ [\text{m}] \end{align}
\(Ro\) が小さいほど、その系でのコリオリの力の影響力が強いことを表します。系の回転の速さを上げると当然その影響力は強くなるので、\(\Omega\) が分母にあります。一方で、\(\Omega\) が一定の場合、対流が激しいほどコリオリ力の影響は無視でき、流速が遅いほどコリオリの力の影響は強く出るため、\(V\) が分子に現れています。
図 17 の (a) の計算結果は \(Ro = 0.09\)、(b) は \(Ro = 4\) です。\(Ro\) が大体 1 を超えると、(a) のパターンから (b) のパターンに移行します。太陽に似せた設定でのシミュレーションで典型的に得られる値として \(V \sim 200 \ \text{m s}^{-1}\), \(L \sim 3 \times 10^{7} \ \text{m}\) を代入し、太陽の自転角速度 \(\Omega = 2.7 \times 10^{-6} \ \text{rad s}^{-1}\) を用いると、\(Ro \sim 1.2\) となります。これは (a) と (b) のちょうど中間的な状態です。
太陽に似せた設定での全球シミュレーションでは、しばしば十分に赤道が加速されなかったり、極が加速されて太陽とは逆の差動回転パターンが形成されてしまいます。つまり、どちらかというと (b) に近い結果が得られてしまうわけです。実際の太陽のような差動回転を得るために、系を太陽よりも速く回転させたり、内部から与える熱量を減らして対流を抑えることで、 \(Ro\) をわざと小さくしている研究も多いです。
つまり、現在のシミュレーションは熱対流の速さ (激しさ) を過大評価しているかもしれないのです。別の言い方をすると、実際の太陽内部の熱対流は、シミュレーションよりも遅い速度であるにも関わらず、同じだけの熱エネルギーを表面まで輸送できるような別の状態にあるかもしれません。
日震学による対流構造の推定にはまだ大きな不確かさがありますが、シミュレーション結果よりも対流が穏やかであることを示唆する報告もあります。
今までの説明では「磁場」という言葉が出てきませんでしたが、現実の太陽は磁場を持っています。対流層を構成する気体は電気を通しやすい性質を持っているため、磁場が存在すれば熱対流はそれに影響を受け、逆に磁場にも影響を与えるでしょう。その影響を調べることがこの問題の解決につながるのではないかと考える研究者もいます (詳しくは例えば Karak et al., 2018 の Introduction を読んでください)。
子午面環流がまばら?
図 17 の右側で差動回転を表す色に重ねて描かれた黒い曲線は、得られた子午面環流の流れ方 (流線) を表しています。(b) では子午面環流は各半球に 1 つずつの大きな流れで存在していますが、(a) の場合は小さな環流がたくさん存在していることが分かります。
この傾向も多くの全球シミュレーションで見られます。差動回転が太陽と逆の場合は、むしろ現実的な子午面環流が形成されるのに、赤道が速く回っている場合は小さな環流に分かれてしまうのです。
子午面環流は、系の状況に応じて繊細にその形状を変えると考えられます。既述したように、日震学による子午面環流の推定に大きな不確かさがあることも、この問題を難しくしています。
表面の熱対流との関係
表面の熱対流の計算では、光として逃げて行くエネルギーや
部分電離
脚注
[電離]:粒子が電子を手放して電荷を持つようになることを電離と言います。電荷を持った粒子を含む気体をプラズマと言います。一部の粒子のみが電離している状態を部分電離または弱電離と言います。
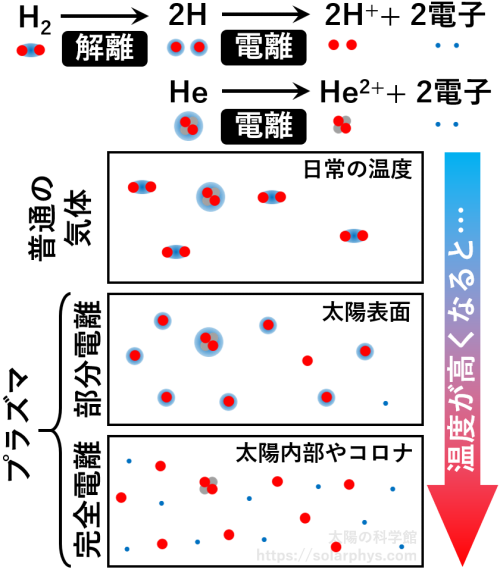 など、太陽内部より複雑な物理を考慮に入れねばなりません。また、全球シミュレーションで用いる方程式は、広い領域での計算を短時間で可能にするための単純化が施されているため、粒状斑のような激しい対流の計算には向きません。このように、対流層の内部と表面を同時に計算することは難しく、現在の全球シミュレーションでは \(0.95 - 0.98 R_\odot\) の領域までしか計算することができません。更に、現在の全球シミュレーションが達している解像度は数千 km 程度なので、まだ超粒状斑のスケール (3 万 km 程度) の現象を詳しく調べるには心許ない粗さです。
など、太陽内部より複雑な物理を考慮に入れねばなりません。また、全球シミュレーションで用いる方程式は、広い領域での計算を短時間で可能にするための単純化が施されているため、粒状斑のような激しい対流の計算には向きません。このように、対流層の内部と表面を同時に計算することは難しく、現在の全球シミュレーションでは \(0.95 - 0.98 R_\odot\) の領域までしか計算することができません。更に、現在の全球シミュレーションが達している解像度は数千 km 程度なので、まだ超粒状斑のスケール (3 万 km 程度) の現象を詳しく調べるには心許ない粗さです。
これらの困難がどの程度の要因になっているのかは分かりませんが、全球シミュレーションで得られる表面付近の対流は超粒状斑のスケールより大きくなっています。実際の太陽では、運動エネルギーの観点から見ると、超粒状斑より大きなスケールでの対流は存在しません。
この傾向は別の種類のシミュレーションでも見られます。粒状斑の記事 で説明していますが、粒状斑は太陽表面の一部を切り取ったような領域でのシミュレーションによって、上手く再現されています。しかし、この類のシミュレーションの領域を広くしていくと、超粒状斑より大きなスケールでの対流が起きてしまうという報告もあります。
この問題は上述した過大評価の問題と関係しているかもしれません。つまり、内部対流が抑えられれば、それに伴って表面での大きな対流もなくなり、今まで隠れていた超粒状斑が顔を出すのではないかと考える研究者もいます ( この問題も含めて超粒状斑について詳しくは Rincon & Rieutord, 2018 )。
極と赤道の温度差の原因
日震学によって推定された差動回転の構造 ( 図 2 ) と 図 17 (a) で得られている構造を見比べると、大きな違いは次の 2 つでしょう ( 図 18 )。
- シミュレーションで得られる自転角速度の等値線は、自転軸に平行であるのに対して、実際の太陽の等値線は傾いている (図のオレンジ)。
- シミュレーション結果では速度勾配層が再現されていない (図の赤)。
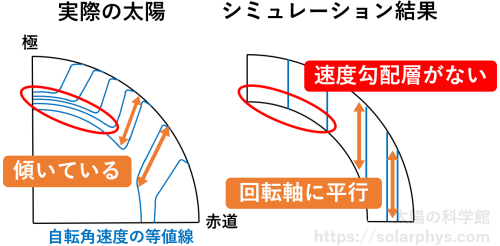
図 17 の研究では、速度勾配層より上の対流層を模した領域だけを想定した問題設定なので、そもそも速度勾配層の再現を試みていません。よって 2 の違いが現れるのは想定内ですが、そのようなシミュレーションでは、同時に 1 の違いも現れる傾向にあります。
様々な研究から、極が赤道よりも 10 \(\text{K}\) ほど暖かければ、1 の違いを回避できることが分かっています。対流層は基本的に 100 万 \(\text{K}\) 程あることを考えると、これは非常に小さな差です。その温度差が生む水平方向の小さな圧力差とコリオリ力の間の繊細なバランスによって、差動回転の等値線が自転軸方向から傾きます。
問題は何がこの 10 \(\text{K}\) の温度差を生んでいるのかです。熱対流はそもそも熱を表面 (鉛直上向き) に向かって輸送する働きをしますが、そこにコリオリの力が働くと、極方向にも熱を運ぶようになることは知られています。しかし、図 17 のようなシミュレーションでは、その効率が不十分なため、それによって 10 \(\text{K}\) の大きさの温度差を生むことはできず、1 の違いが表れています。
この問題の解決案としては、例えば次の 2 つの方向性の研究があります。
- 速度勾配層まで再現した研究では、極が十分に温められている ( 例えば Brun et al., 2017 )。速度勾配層で強い加熱が起こることで、高緯度の加熱を助長している可能性がある。
- 熱対流と磁場の相互作用まで考慮すると、対流の性質が変化して、極に熱を運ぶ効率が高まる可能性がある ( Hotta, 2018 )。
内側の一様回転の謎
太陽内部の流れにまつわる謎は、対流層の差動回転だけではありません。日震学の推定 ( 図 2 ) によると、半径 \(0.7 R_\odot\) より中心に近い領域は一様な (各場所で等しい) 角速度で自転しているのでした ( 図 19 の紫 )。この一様回転は少なくとも \(0.3 R_\odot\) まで続いているようです。

この \(0.7 R_\odot\) より深い領域は
放射層
脚注
[放射層]:太陽半径を \(R_\odot =\) 約 70 万 km としたとき、 \(0.715 R_\odot\) より内側の領域を指します。この領域では主に光の放射と吸収によってエネルギーが外側へと運ばれます。特に中心付近の核融合が起きている領域をコアと呼ぶこともあります。
 と呼ばれ、熱対流が起きない領域です。よって、上の節で説明した機構は働かないため、強い差動回転が存在しないことは自然に感じられます。しかし、太陽の進化と共に表面から角運動量が失われていくという立場に立てば、やはり中心に近づくほど速く回転している構造でも良いような気がします。実際に、素朴な理論に基づいて、放射層の 46 億年の進化を概算すると、中心が速くなるような回転構造が得られます。
と呼ばれ、熱対流が起きない領域です。よって、上の節で説明した機構は働かないため、強い差動回転が存在しないことは自然に感じられます。しかし、太陽の進化と共に表面から角運動量が失われていくという立場に立てば、やはり中心に近づくほど速く回転している構造でも良いような気がします。実際に、素朴な理論に基づいて、放射層の 46 億年の進化を概算すると、中心が速くなるような回転構造が得られます。
放射層が一様回転していることは、対流層との間に速度勾配層 ( 図 19 の赤 ) が形成されていることとも密接な関係にあります。急な速度勾配は不安定化しやすいため、対流層の差動回転が放射層をもっと侵食しても良い気がします。しかし、現実には放射層が断固として一様回転を保持し、薄い (急激な) 速度勾配層を形成しています。
対流層の下に放射層の一部を設置した全球シミュレーションでは、一時的に速度勾配層を再現することはできますが、そのようなシミュレーションは精々 100 年分程度を計算するのが限界です。仮にもっと長い期間 (1000 年分とか) に渡って計算を続けると、再現された速度勾配層は徐々に放射層を侵食して広がっていくだろうと考えられています ( Brun et al., 2011 )。
この問題については様々な可能性が考えられていますが、実際の太陽の特徴を十分に説明できるシナリオは得られていないようです ( 詳しくは例えば Aerts et al., 2019, Hughes et al., 2007 )。
例えばこれまで提唱されたシナリオの 1 つには次のようなものがあります。11 年周期の記事 で説明していますが、現在対流層に存在していて、ときに黒点や活動領域として我々が見ることのできる磁場は、対流層内部の流れによって 10 年の時間スケールで生成・維持されています。一方で、放射層には、 46 億年前の太陽形成時に物質と共に内部に引き込まれた磁場の一部 (化石磁場) が現在まで閉じ込められている可能性があります。

記事「プラズマと磁場:磁力線が「実体」を帯びる」で説明しているように、太陽を構成する
プラズマ
脚注
[プラズマ]:粒子が電子を手放して電荷を持つようになることを電離と言います。太陽内部やコロナは温度が高いので、主な構成元素である水素やヘリウムは、電離してイオンの状態で存在します。電荷を持った粒子を含む気体をプラズマと言います。太陽表面は温度が不十分なので、一部の粒子のみが電離しています。この状態を部分電離と言います。
 中では、
磁力線
脚注
[磁力線]:各場所での磁場の向きを繋げた曲線を磁力線と言います。理想的には磁力線の密集度がその場所での磁場の強さ (単位 T, テスラ) を表しますが、実際の図では特徴的な磁力線だけを間引いて描くため、この限りではありません。磁力線が分裂したり合流したりすることはありません。電気を通すプラズマでは磁力線は物質に凍結している (物質は磁力線に垂直な方向に動くことができない) ので、磁力線の動きはその場所でのプラズマ (物質) の動きを表します。
中では、
磁力線
脚注
[磁力線]:各場所での磁場の向きを繋げた曲線を磁力線と言います。理想的には磁力線の密集度がその場所での磁場の強さ (単位 T, テスラ) を表しますが、実際の図では特徴的な磁力線だけを間引いて描くため、この限りではありません。磁力線が分裂したり合流したりすることはありません。電気を通すプラズマでは磁力線は物質に凍結している (物質は磁力線に垂直な方向に動くことができない) ので、磁力線の動きはその場所でのプラズマ (物質) の動きを表します。
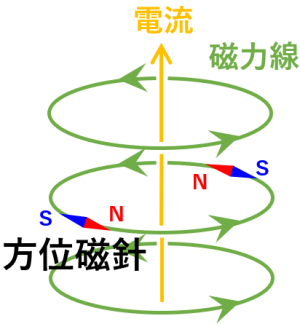 は気体に対して相対的に動くことができないという性質を持ちます。つまり、化石磁場が存在すれば、放射層は磁力線という「串」に刺された状態になります。仮に 図 20 の左のように、化石磁場の磁力線が完璧に放射層内に閉じ込められていれば、放射層は芯の通った球体として一様に回転するかもしれません。
は気体に対して相対的に動くことができないという性質を持ちます。つまり、化石磁場が存在すれば、放射層は磁力線という「串」に刺された状態になります。仮に 図 20 の左のように、化石磁場の磁力線が完璧に放射層内に閉じ込められていれば、放射層は芯の通った球体として一様に回転するかもしれません。
この説のキーポイントは、化石磁場が完全に放射層に閉じ込められるのかどうかです。子午面流によって抑え込むことができるかもしれないという予想もありますが、この説を検証するための全球シミュレーションでは、 図 20 の右のように、極から化石磁場が対流層に顔を出してしまいます。その結果、磁力線に沿って放射層が持つ角運動量が流出し、軸に近い部分の自転が遅くなってしまうようです ( Strugarek et al. 2011 )。
参考文献
記事全体として参考にしたレビュー (書籍)
- Brun, A. S. and Rempel, M. (2009). Large scale flows in the solar convection zone. Space Science Reviews, 144, 151–173 .
- Hanasoge, S., Miesch, M. S.,Roth, M., Schou, J., Schüssler, M. and Thompson, M. J. (2015). Solar dynamics, rotation, convection and overshoot. Space Science Reviews, 196, 79–99 .
- Rüdiger, G., Kitchatinov, L. L. and Hollerbach, R. (2013). Magnetic Processes in Astrophysics: Theory, Simulations, Experiments (Weinheim: Wiley-VCH ).
引用した文献
- Aerts, C., Mathis, S. and Rogers, T. M. (2019). Angular momentum transport in stellar interiors. Annual Review of Astronomy and Astrophysics, 57, 35-78 .
- Brun, A. S., Miesch, M. S. and Toomre, J. (2011). Modeling the dynamical coupling of solar convection with radiative interior. The Astrophysical Journal, 742, 79 .
- Brun, A. S., Strugarek, A. Varela, J., Matt, S. P., Augustson, K. C., Emeriau, C. DoCao, O. L., Brown, B. and Toomre, J. (2017). On differential rotation and overshooting in solar-like stars. The Astrophysical Journal, 836, 192 .
- Gallet, F. and Bouvier, J. (2013). Improved angular momentum evolution model for solar-like stars. Astronomy & Astrophysics, 556, A36 .
- Gastine, T., Yadav, R. K., Morin, J., Reiners, A. and Wicht, J. (2013). From solar-like to antisolar differential rotation in cool stars. Monthly Notices of the Royal Astronomical Society: Letters, 438, L76–L80 .
- Gizon, L., Cameron, R. H., Pourabdian, M., Liang, Z.-C., Fournier, D., Birch, A. C. and Hanson, C. S. (2020). Meridional flow in the Sun’s convection zone is a single cell in each hemisphere. Science, 368, 1469-1472 .
- Hotta, H. (2018). Breaking Taylor–Proudman balance by magnetic fields in stellar convection zones. The Astrophysical Journal Letters, 860, L24 .
- Hotta, H., Rempel, M. and Yokoyama, T. (2015). High-resolution calculation of the solar global convection with the reduced speed of sound technique. II. Near surface shear layer with the rotation. The Astrophysical Journal, 798, 51 .
- Hughes, D. W., Rosner, R. and Weiss, N. O. (Eds.). (2007). The Solar Tachocline ( Cambridge: Cambridge University Press ).
- Karak, B. B., Miesch, M. and Bekki, Y. (2018). Consequences of high effective Prandtl number on solar differential rotation and convective velocity. Physics of Fluids, 30, 046602 .
- Mandal, K., Hanasoge, S. M., Rajaguru, S. P. and Antia, H. M. (2018). Helioseismic inversion to infer the depth profile of solar meridional flow using spherical Born kernels. The Astrophysical Journal, 863, 39 .
- Nordlund, Å., Stein, R. F. and Asplund, M. (2009). Solar surface convection. Living Reviews in Solar Physics, 6, 2 .
- Rincon, F. and Rieutord, M. (2018). The Sun’s supergranulation. Living Reviews in Solar Physics, 15, 6 .
- Strugarek, A., Brun, A. S. and Zahn, J.-P. (2011). Magnetic confinement of the solar tachocline: II. Coupling to a convection zone. Astronomy & Astrophysics, 532, A34 .