黒体放射

熱いと光る

太陽は常に明るく輝いています。太陽の発した光の一部は地球の大気に吸収されたり反射されたりしますが、ほとんどは地上まで降り注ぎ、我々の周りを照らしています。部屋の壁が電灯の光を反射して明るく見えるように、月は太陽の光を反射しているため明るく見えます。対して太陽は、電灯と同じように自ら光っています。

身の回りで自ら光るものと言えば、電灯や炎、スマホの画面などがあります。これらの光は、原子や分子が発しています。例えば蛍光灯の場合は、ガラス管の内面に塗られた蛍光物質を構成する原子や分子、あるいは炎の場合は、燃料が燃えて熱くなった部分に存在する原子や分子が発した光が目に届きます。太陽が光る仕組みも基本的にはこれらと同じです。

図 1 は三鷹にある国立天文台の望遠鏡によって 白色光 脚注 [白色光]：特殊なフィルターを通していない光 (可視光) を撮影したという意味です。 で撮影された太陽表面です。図を見ると、はっきりとした表面が確認できます。我々が眩しいと感じる光のほとんどはこの表面から発せられています。

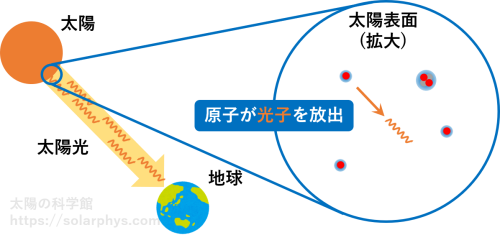
太陽表面を構成する原子や分子の一個一個は「光子 (photon)」と呼ばれる短い光を勝手なタイミングで発しています ( 図 2 )。太陽表面にはたくさん (\(1 \ \text{cm}^3\) あたりに \(10^{17}\) 個程度) の粒子が存在するため、発せられる光子の数も膨大になります。それらの光子の集団の一部が約 8 分かけて地球まで届き、我々の目に飛び込むことで、我々は眩しいと感じるわけです。

では、例えば壁や人間の体は光らないのに、なぜ電灯や炎、太陽は光っているのか？という疑問が湧きます。物が光る仕組みは大きく「熱放射」と「それ以外」に分けることができます。太陽や炎、白熱灯などは熱放射です。対して、蛍光灯や LED などは熱放射ではありません。

物質は熱くなると光ります。これが熱放射です。熱した鉄は赤く光ります。白熱灯は、フィラメントが電気抵抗によって熱くなることで光ります。太陽表面も約 \(6000 \ \text{K}\) ( ケルビン 脚注 [ケルビン]：温度の単位には基本的にケルビン (K) を用います。日常で使われる摂氏と目盛の幅は同じであり，摂氏 0 度は 273.15 K です。つまり，例えば 300 K は摂氏 26.85 度のことです。 ) の熱さであるため、光っています。

なぜ熱くなると光るのかについて詳しくは下の節で説明しますが、大雑把には次の理屈です。物質はたくさんの原子や分子のような粒子でできています。ただし、ここでは気体の場合を想定して説明します。各粒子はエネルギーの「高い状態」と「低い状態」をとり得ます。各粒子が飛び交う中で、粒子同士の衝突が頻繁に起きます。このときに、衝突相手の粒子からエネルギーをもらったり、逆に与えたりすることで、「高い状態」と「低い状態」の間の変化を繰り返しています。両者の存在比は温度で決まり、熱くなる程前者の割合が増えます ( 図 3 A )。

「高い状態」にある粒子は光子を放出することで「低い状態」に変化することがあります ( 図 3 B )。対して、「低い状態」にある粒子は、光子を吸収して「高い状態」に変化することはあれど、光子の放出に利用できるエネルギーは持ち合わせていません。温度が高いほど光子を放出できる粒子の割合が増えるので、物質は明るく光ります。

この理屈でいくと、人間の体もある程度の温度を持っているため、太陽や電灯ほど明るくないにせよ、いくらか光っていることになります。目では分かりませんが、 赤外線 脚注 [赤外線]：電磁波 (光) のうち、波長が大体 780 nm から 0.1 mm の領域のものを赤外線と言います。波長帯によっては地球大気に吸収されます。 カメラで見ると、実際に光っている様子を確認できます。その光の量から温度を推定する技術がサーモグラフィーです。

蛍光灯や LED などは、物質を熱くする以外の方法で、むりやり「高い状態」の粒子を増やすことで光らせています。その手法は装置によって様々です。

太陽の放射スペクトル

光は波長という性質を持ちます。色のことです。記事「光とは何か？」でも説明していますが、我々人間は波長が大体 400 nm から 800 nm の光のみを見ることができます。この波長領域の光は可視光と呼ばれます。可視光より短い波長の光は紫外線、X 線などと呼ばれ、逆に長い波長の光は赤外線、電波と呼ばれます ( 図 4 )。

各波長ごとの光の強度を表すグラフをスペクトルと言います。太陽光のスペクトルを 図 5 に示しました。横軸は波長、縦軸はその波長の光の強度を表します。

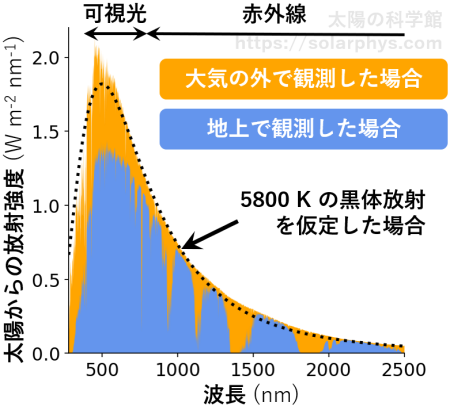
図を見ると、太陽は主に可視光領域の光を強く放っていることが分かります。図にオレンジ色で示したスペクトルは、観測衛星が地球大気の外で観測したときの光です。これは太陽が放っている光と同じであると考えられます。一方で、青色で示したスペクトルは、地上で太陽光を観測した場合のものです。太陽光の一部は地球大気で吸収・反射されるため、地上で観測される光はその分弱くなっています。特に赤外線の一部の波長帯の光はほとんど地上に届いていないことが分かります。

また、特に波長の短い紫外線や X 線も大気で吸収されるため、地上には届きません。これらの光は人体に有害なため、我々は大気に守られているとも言えます。一方で、記事「太陽七変化：様々な光で見た姿」で説明していますが、 X 線を用いると太陽コロナを観測することができます。しかし地上には届かないため、観測衛星を用いての宇宙からの観測が必須になります。

上の節で、太陽は熱放射と呼ばれる原理で光っていると述べました。もっと細かい話をすると、太陽は熱放射の中でも特に「黒体放射 (black body radiation)」に近い光り方をしています。詳しくは下の節で説明します。

黒体放射をしている物質の明るさ (スペクトル) は、その物質の温度のみで決まります。図 5 に黒い点線で示したのは、太陽が黒体放射で光っている \(5800 \ \text{K}\) の物質であると仮定したときに予想されるスペクトルです。大気の外で観測されたスペクトルは大体点線と形が一致していることが分かります。下の節で詳しく説明しますが、これは太陽表面が大体その温度であることを示しています。

黒体放射の性質

太陽のスペクトルは黒体放射のそれによく似ていることを述べました。身の回りでは、例えばろうそくの炎のような黄色い (赤い) 炎は黒体放射に比較的近いスペクトルを持っていると思われます。ガスコンロの青い炎は黒体放射ではありません ( 図 6 )。

黒体放射をしている物質の明るさ (スペクトル) は、その物質の温度のみで決まり、密度や物質の種類には依存しません。つまり、同じ温度・形の物体が、同じだけ離れた場所で黒体放射によって光っていたら、皆同じ明るさに見えます。図 7 に様々な温度での黒体放射のスペクトルを描きました。

図 7 に赤色で描いた線は 図 5 の点線と同じ 5800 K の黒体放射です。ただし、こちらの図は広い範囲を描くために横軸・縦軸共に対数スケールを用いています。そのため、図 5 とは違う形に描かれています。

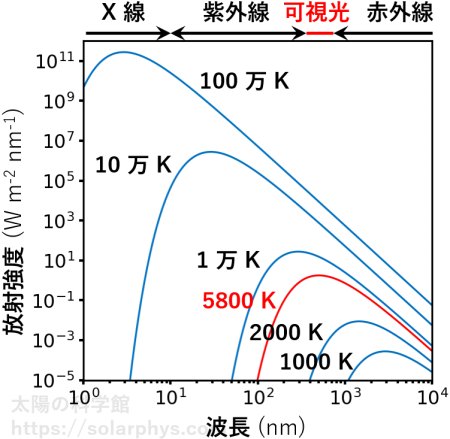
図を見ると、温度が高くなる程黒体放射の強度は大きくなり、より波長の短い光を中心に光ることが分かります。

図 6 のろうそくの炎では、燃焼で発生したすす (炭素の塊) が大体 \(1000 \ \text{K}\) 程度に熱せられることで、黒体放射に近い光を発しています。図を見ると、この温度は主に赤外線を発していることが分かります。可視光の領域では波長の長い光をより多く発しているため、暖色に見えます。

因みに、コンロの炎では、燃料のガスが燃える際に生成される \(\text{CH}\)、\(\text{C}_2\) のような粒子が青い光を発しています。これは黒体放射とは異なり、光る物質の種類に依存した光です。

太陽光は約 \(6000 \ \text{K}\) の黒体放射に近似することができ、この \(6000 \ \text{K}\) とは、表面の物質の温度を意味すると述べました。このことは夜空に輝く他の恒星の場合も同じです。ただし、表面温度は恒星によって異なります。そのため、恒星はそれぞれ別の色に輝きます。有名な恒星について、表面温度と光度のデータと色を 表 8 に示しました。表面温度の低い星は赤色、高い星は青色に輝きます。

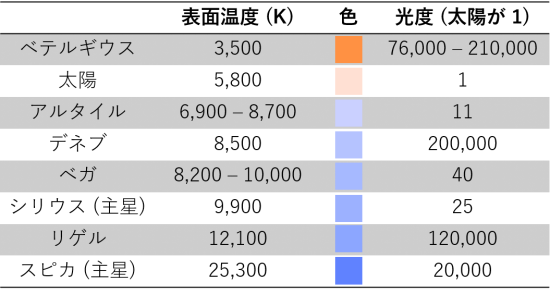
光度とは、恒星が単位時間あたりに光として失うエネルギーの大きさです。詳しくは記事「基本構造：何からできているのか？」で太陽の場合について説明していますが、地球から見える恒星の明るさと恒星までの距離が観測から得られれば光度を計算できます。

光る面が多ければ多いほど、恒星はたくさんエネルギーを失うので、光度は恒星の表面積に比例します。恒星はおよそ球体であると仮定すれば、光度 \(L\) は半径 \(R\) の 2 乗に比例することになります。

\[L\propto R^2\]

\(\propto\) は「比例する」という意味の記号です。一方で、黒体放射は既に述べたように、温度のみに依存します。具体的には、単位面積あたりに放出される光のエネルギーは温度の 4 乗に比例します (シュテファン-ボルツマンの法則)。よって、恒星が黒体であると仮定すれば、光度を表面積で割った値は表面温度 \(T\) の 4 乗に比例するはずです。

\[\frac{L}{R^2}\propto T^4\]

この関係を用いれば、恒星の表面温度と光度から半径を推定することができます。例えばベテルギウスは太陽の

\[\frac{3500}{5800}=0.60\]

倍の表面温度を持つので、\(L/R^2\) の値は太陽の \((0.60)^4\) 倍であるはずです。一方で、表を見ると、光度は太陽の 8 万から 21 万倍程度です。仮に13 万倍とすると、\(R^2\) は太陽の

\[\frac{130000}{(0.60)^4}=1.0 \times 10^6\]

倍であると計算できます。ここから、ベテルギウスの半径は太陽の約 1000 倍であると推定できます。

最新の望遠鏡は高解像度なので、ベテルギウスの形まで観測できます。つまり、半径を直接測定することができます。図 9 にアルマ望遠鏡で捉えられたベテルギウスの姿を示しました ( 図の色について 脚注 [図の色]：図に映っているベテルギウスの色は人工的に着けられたものです。惑わされないでください。この図は、電波 (波長の長い光) によって撮影されたものであり、得られた光の強度を慣習に従った色によって図示しています。 )。この画像の解析 ( Kervella et al., 2018 ) によると、画像で見えているベテルギウスの半径は太陽の 1400 倍ほどです。アルマ望遠鏡は電波で見ているので、図 9 ではベテルギウスの表面よりいくらか外側が映っていますが、大体上で推定した値と同じくらいの大きさです。

黒体放射とは何か 1 ：熱平衡

今まで説明してきたように、黒体放射には次の性質があるのでした。

1. ある波長にピークを持つようなスペクトルを放つ。
2. スペクトルの形と放射光の強度 (明るさ) は光を放っている物質の温度のみに依存し、物質の種類には依らない。
3. 温度が高いほど強く光る。
4. スペクトルのピークは温度が高いほど波長の短い側に移動する。

特に 2 番目の性質は、よく考えると大胆なことを言っています。世界には様々な色の物質が存在していますが、条件を満たして黒体放射を始めれば、どんな物質でも皆同じ色で光るわけです。黒体放射について深く考えると、この世界を支配する不思議な物理法則の一端を見ることができます。

ある物質が黒体放射をするためには、次の 2 つの条件が必要です。

1. その物質が (局所) 熱平衡状態にある。
2. その物質が十分に不透明である。

これらの条件の意味を説明することで、黒体放射についての理解を深めます。

熱平衡

太陽は気体です。詳しくは 基本構造の記事 で説明していますが、太陽表面は 図 10 のように、基本的には水素原子とヘリウム原子が飛び交い、偶により重い元素から成る粒子も飛び交っているような状態になっています。また、稀に 電離 脚注 [電離]：粒子が電子を手放して電荷を持つようになることを電離と言います。電荷を持った粒子を含む気体をプラズマと言います。一部の粒子のみが電離している状態を部分電離または弱電離と言います。 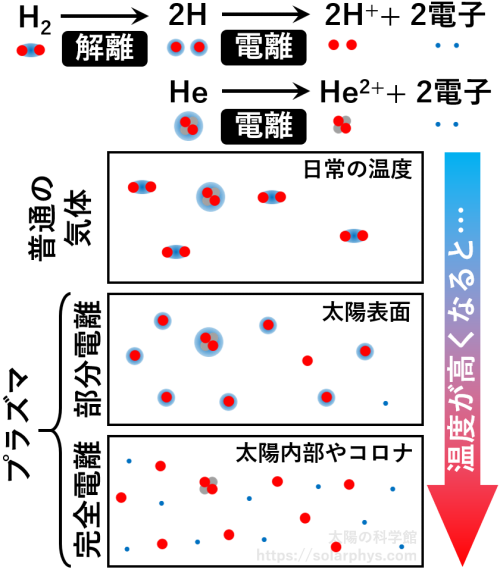した水素イオン (陽子) や電子なども飛んでいます。更に、これらの物質粒子が発した短い光である光子も飛び交っています。光子について詳しくは 光の記事 でも説明しています。太陽表面での物質粒子の数は \(1 \ \text{cm}^3\) あたりに \(10^{17}\) 個程度です。

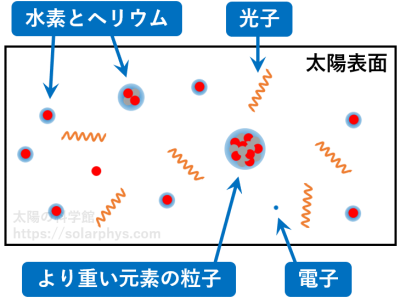
図には電子のイメージを青色で描きました。原子は原子核と電子から成ります。原子核を電子が覆っているとイメージしてください。整理すると、電子は原子に束縛された状態でも存在しますし、独立した粒子としても存在します。前者を束縛電子、後者を自由電子と呼ぶことにします。

このように太陽表面では様々な粒子が各々勝手に飛び交っているので、粒子同士の衝突が頻繁に起きます。例えば次のような衝突です。

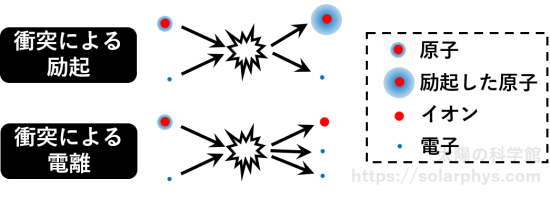
図 11 のように、原子が自由電子と衝突すると、自由電子のエネルギーの一部が、原子に束縛された電子に奪われることがあります。束縛電子はエネルギーをもらうと、その軌道が膨らみます。このように、束縛電子が元気な状態の原子を「励起」した状態と言います。あるいは、衝突によって束縛電子が大きなエネルギーを得た場合には、原子核の下を離れて自由電子になることもあります (電離)。

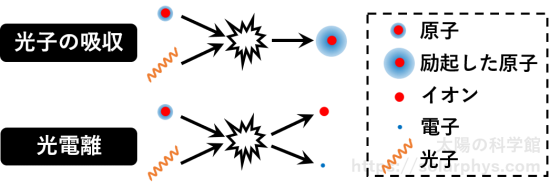
励起や電離は光子との衝突によっても起きます ( 図 12 )。それぞれ、吸収、光電離と呼ばれる反応です。衝突した光子は全てのエネルギーを束縛電子に与えて消滅します。

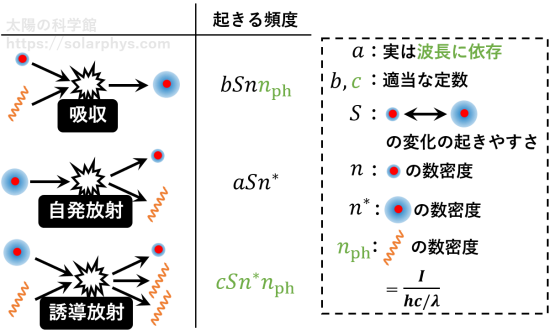
励起した原子やイオンが存在すると、図 13 のような反応も起きます。励起した原子と自由電子が衝突すると、束縛電子のエネルギーの一部が自由電子に奪われ、励起していない元の原子に戻ることがあります。これを衝突による脱励起と言います。励起した状態は、束縛電子がエネルギーを持て余している状態なので、不安定です。そのため、励起した原子は時間が経つと自ら光子を放出し、励起前の原子に戻ります (自発放射)。あるいは、光子との衝突に伴って脱励起することもあります (誘導放射)。イオンと自由電子が衝突すると、電子がエネルギーを失って原子に束縛される代わりに、光子を放出することがあります (再結合)。

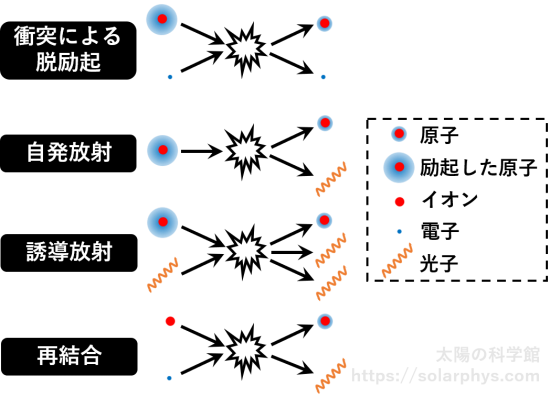
更には、例えば 図 14 のように、イオンと自由電子の衝突に伴って電子のエネルギーの一部が光子に変換されること (制動放射) や、イオン、自由電子、光子の 3 粒子が衝突することで光子が電子に吸収されること (自由-自由吸収) などもあります。起きうる反応の種類はまだ他にもあります。

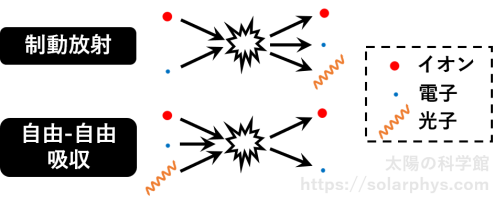
以上、たくさん羅列しましたが、太陽表面ではこのように、様々な種類の反応がそれぞれ勝手な場所で確率的に起きています。起きる確率は反応の種類や関係する原子 (あるいは分子) 種ごとに違います。存在している粒子数も原子種ごとに異なるため、それぞれの反応が単位時間・単位体積あたりに起きる数は千差万別です。

ある種の衝突が起きる頻度は、衝突する 2 つの粒子の数密度 (単位体積あたりの粒子数) の積に比例します。例えば上で挙げた中の衝突による励起の場合には、(励起していない原子の数密度)\(\times\)(自由電子の数密度) です。数密度が多くなる程出会う確率が高くなるわけです。

説明を簡単にするために、衝突による励起と脱励起のみを考えます ( 図 15 )。仮に励起していない原子の数が多ければ、脱励起より励起の起きる頻度の方が高くなります。よって、励起がどんどん進み、励起していない原子の数は減って、励起した原子の数が増えます。励起した原子の数が多かった場合には、逆の事態が起きます。

このように、励起していない原子と励起した原子の数がアンバランスだった場合は、多い方を少なくして、少ない方を多くしようとする機構が働きます。これを緩和と言います。太陽表面や通常の空気のような十分に濃密な気体では衝突は頻繁に起きているので、何らかの原因で両者の数密度がアンバランスになっても、すぐに緩和が起きて元のバランスに戻ります。この状態を (局所) 熱平衡と言います。

特定の原子種 (例えば水素原子) に注目すると、熱平衡にある物質中では、励起していない状態と励起した状態の数密度の比は、温度のみによって決まります。詳しい計算方法は省きますが、例えば温度が 6000 K のときの比は

\[\frac{\text{励起した水素原子の数密度}}{\text{励起していない水素原子の数密度}}=4\times 10^{-4}\]

と計算することができます。具体的な励起・脱励起の反応の性質に依らず、この比に落ち着きます。温度が高くなる程、この比は大きくなります。

熱放射

熱平衡にある物質からの放射を熱放射と言います。上で挙げた様々な反応の中には、反応前後で光子が 1 個増えるものと、逆に 1 個減るものがあります。以下、特定の原子種による光子の吸収と自発放射のみに注目します ( 図 16 )。

例えば水素原子の場合は 410 nm, 434 nm, 486 nm, ... と、その原子種が励起・脱励起に伴って吸収または放射し得る光子の波長は決まっています。これについて詳しくは記事「スペクトル線：なぜ様々な光で観測するのか？」で説明しています。ここではとりあえず、その原子種が吸収・放射し得る特定の波長の光子のみに注目します。

先ほども述べたように、反応の起きる頻度は反応前の関係する粒子の数密度に比例します。光子の数密度とは、すなわち光の強度 (明るさ) のことです。吸収と放射の頻度は共に、未励起の状態と励起状態をどれだけ行き来しやすいかの指標である「線強度 \(S\)」という量にも比例します。\(S\) は原子種によって異なる値を持つ量です。以上のことを踏まえると、各反応が起きる頻度は 図 16 のように書けます。\(a,b\) は適当な定数です。

今後のために、\(bSn=\alpha\)、\(aSn^*=\varepsilon\) と書くことにします。つまり、吸収と放射の起きる頻度はそれぞれ \(\alpha I\) と \(\varepsilon\) です。\(\alpha\) と \(\varepsilon\) の比は

\[\frac{\varepsilon}{\alpha}=\frac{aSn^*}{bSn}=\frac{a}{b}\frac{n^*}{n}\]

と約分できます。更に、物質が熱平衡ならば、\(n^*/n\) は温度のみに依存するため、適当な温度 \(T\) のみの関数 \(B(T)\) を用いて、

\[\frac{\varepsilon}{\alpha}=B(T)\]

と書けます。吸収や放射が起きる頻度自体は原子種によって違いますが、上式の比は原子種の個性に依存しません。今は光子の吸収と自発放射 (議論を簡単にするために誘導放射は無視しています) について考えましたが、他の反応、例えば光電離と再結合の組 ( 図 17 ) を考えた場合でも、同様の考察によってそれぞれの頻度が \(\alpha I, \varepsilon\) という形に書け、熱平衡では同じ関数 \(B(T)\) に対して上式の関係が成り立つことが分かります。これが後に述べるように、上で説明した黒体放射の性質 2 の根本であり、キルヒホッフの法則と呼ばれます。関数 \(B(T)\) はプランク関数と呼ばれます。プランク関数の波長依存性は後から説明します。

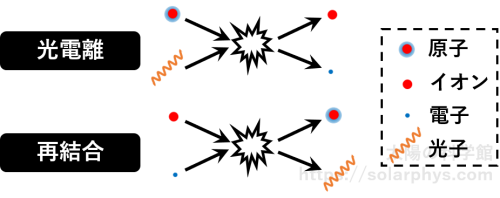
黒体放射とは何か 2 ：不透明

上の節に引き続き、特定の波長の光子のみに注目して議論します。黒体放射の波長依存性については後から説明します。

上の節では、熱平衡にある物質中で光子の吸収と放出が起きる頻度について考えました。光子の放出の頻度は光の強度 \(I\) には依存しませんが、吸収は光子との衝突によって起きるものなので、その頻度は \(I\) に比例するのでした。物質が最終的に放射する光の強度 \(I\) の値は、この 2 つの頻度のバランスによって決まります。\(I\) が黒体放射になるためには、更に、物質が十分に不透明であるという条件が必要です。この条件の意味を説明します。

不透明

我々が太陽を観測したときに見る光は、観測機の視線に沿って、視線とは逆向きに太陽から飛んで来た光子の集団です ( 図 18 )。この光線に沿った光の強度の変化に注目します。

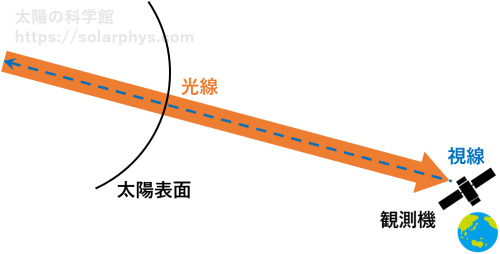
光線の性質を説明するための思考実験として、次の状況を考えます。注目する光線が温度 \(T_\text{m} = 6000 \ \text{K}\) の熱平衡にある物質を突き抜けているとします ( 図 19 )。仮に、入射光の強度 \(I_\text{in}\) が \(B(T_\text{m})\) よりも大きかった場合、次の不等式が成り立ちます。

\[ I_\text{in} > B(T_\text{m}) \ \longleftrightarrow \ \alpha I_\text{in} > \varepsilon \]

これは、光子の吸収が起きる頻度の方が放出の頻度より大きくなることを言っています。よって、光線がこの物質を突き抜けるのに伴って、次の瞬間には光子の数が減ります ( 図 19 の上 )。

逆に、\(I_\text{in}\) が \(B(T_\text{m})\) より小さい場合には、光子の放出の頻度の方が吸収の頻度より大きくなるため、次の瞬間光子の数は増えます ( 図 19 の下 )。このように、物質内では光線の強度に対して緩和が働き、\(B(T_\text{m})\) に近づきます。

不透明な物質とは、吸収が頻繁に起きる物質です。言い換えると、\(\alpha\) が大きい物質です。熱平衡では \(\alpha\) と \(\varepsilon\) の比はある値に定まっているため、そのような物質は \(\varepsilon\) も大きいことになります。不透明な物質では \(B(T_\text{m})\) への緩和が直ぐに起きます ( 図 20 の上 )。よって、出射光の強度は \(B(T_\text{m})\) に一致します。

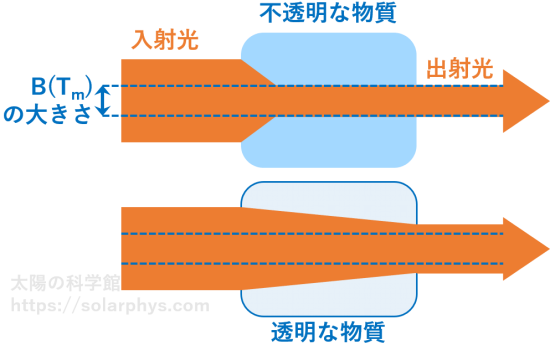
対して、透明な物質では \(I_\text{in}\) が \(B(T_\text{m})\) より大きかったとしても、なかなか光子の吸収が起きないため、緩和がゆっくり進みます。このため、強度が \(B(T_\text{m})\) に一致する前に出射されます ( 図 20 の下 )。つまり、出射光の強度は、入射前の強度の情報を残しています。これが、物質の向こう側が「透けて見える」状態です。

以上、長々と説明してきましたが、熱平衡にある十分に不透明な物質から放たれた光の強度は、その物質の温度 \(T_\text{m}\) に対する \(B(T_\text{m})\) に一致します。これが黒体放射です。太陽表面は約 6000 K なので、その温度に対するプランク関数 \(B(T)\) の強度の光が観測されます。各波長における \(B(5800 \ \text{K})\) の値をプロットしたのが 図 5 の黒い点線です。

温度が高いほど、上の節で述べた数密度比 \(n^*/n\) が高くなるのに伴って \(B(T)\) の値が大きくなるため、物質はより強い光を放射します。

ではコンロの青い炎は何なのか？

ガスコンロの青い炎は黒体放射ではないと述べました。コンロから噴き出した気体 (燃料のガスと空気の混合気体) は十分に濃密なため、熱平衡からはそれほど離れていないと思われます。この意味で、青い炎の光は熱放射と言えそうですが、黒体放射ではありません。これは、気体が透明だからです。

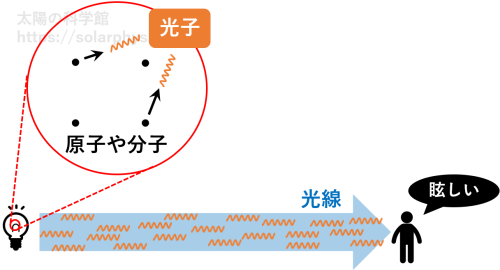
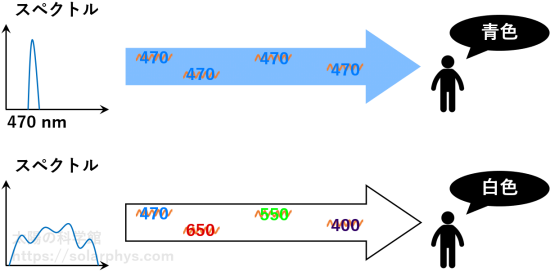
既に説明したように、我々が見る光線は、原子や分子から放出されたたくさんの光子の集団です ( 図 22 )。光子は波長と呼ばれる性質を持ちます。波長は我々が光線を見たときの色に相当します ( 図 23 )。例えば、光線に含まれる光子が全て 470 nm 付近の波長だったならば、光線は全体として青色です。あるいは、光線が可視光域の様々な波長の光子をバランスよく含んでいたならば、その光線は全体として白色に見えるはずです。

原子の励起・脱励起に伴う光子の吸収や放射反応においては、原子種によって決まった波長の光子が消滅・生成されるのでした。例えばメタンガスの燃焼時に生成される \(\text{C}_2\) は 470 nm の光子を吸収・放射します。一方で、例えば光電離や再結合のような反応では、特に決まった値ではなく、広い波長域の光子が消滅・生成されます。

励起や脱励起が起きる頻度は、光電離や再結合が起きる頻度よりずっと高いのが普通です。よって、\(\text{C}_2\) による吸収・放出が起きる 470 nm の光子に対する \(\alpha\) の値は、光電離や再結合のような反応しか起きない波長の光子に対する \(\alpha\) よりもずっと大きくなっています。

このため、光線の中の波長 470 nm の光子のみに注目した場合、緩和は直ぐに起きて出射光は \(B(T_\text{m})\) に一致します。対して、他の波長の光子に対しては、緩和はゆっくり働くため、強度は \(B(T_\text{m})\) に達することができません ( 図 24 )。

従って、炎の形成領域から出射される光線には、波長 470 nm の光子が他の波長の光子に比べてたくさん含まれています。この光線を見た我々は、炎が青いと認識します。他の波長の光に対してはこの炎は透明なので、炎の向こう側が透けて見えます。

太陽表面とは何か

太陽表面とは簡単に言うと、それよりも外側が透明、内側が不透明となっている境界のことです。表面より内側 (太陽内部) は不透明なので、光線の強度は逐次緩和が働いて、常にその場所での物質の温度 \(T\) に対するプランク関数 \(B(T)\) の値にほぼ一致しています ( 図 25 )。

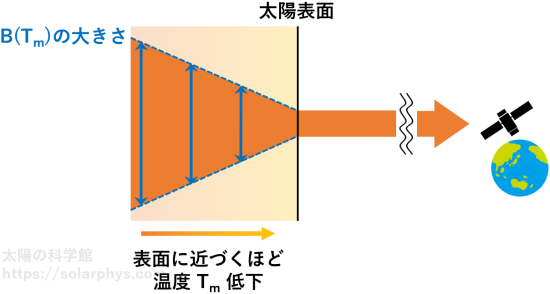
対して、表面より外側 (太陽大気) は透明なので、光線の強度は変化しません。従って、地球に届く光線の強度は、太陽表面の温度、約 6000 K の黒体放射になっています。

不透明とは、光子の吸収反応が起きる頻度 \(\alpha I\) の係数 \(\alpha\) (吸収係数) が十分に大きいという意味でした。この \(\alpha\) は前述したように、吸収時に光子と衝突する相手の粒子の数密度に比例します。太陽は外側に行くほど、気体の数密度が小さくなるので、それに伴って \(\alpha\) の値も小さくなります。

図 26 に、太陽表面付近での気体の数密度と共に、光子の平均自由行程と呼ばれる量を示しました。平均自由行程とは、放出反応で生成されてから別の粒子と衝突して吸収されるまでに光子が進むことのできる平均的な距離です。数密度が低くなる程、吸収が起きる確率が下がるので、平均自由行程は大きくなります。

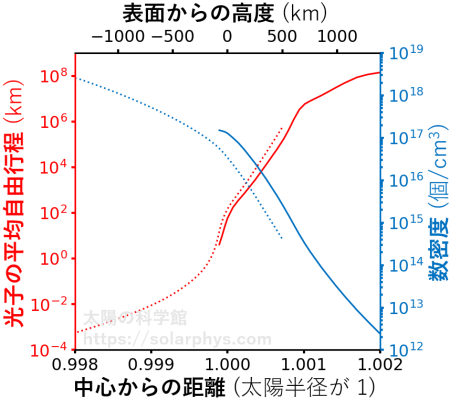
太陽内部での平均自由行程は 100 km よりずっと小さい値です。内部で生成された光子のほとんどは、表面に達する前に吸収されます ( 図 27 )。対して、太陽大気での平均自由行程は 100 km より大きな値です。よって、表面で生成された光子の大部分が吸収されずに (表面からの) 高度 1500 km 程度まで達することができます。そのあたりの平均自由行程は \(10^8 \ \text{km}\) (\(\simeq\) 太陽と地球間の距離) になっているため、達した光子はその後、吸収されることなく地球に到達できます。

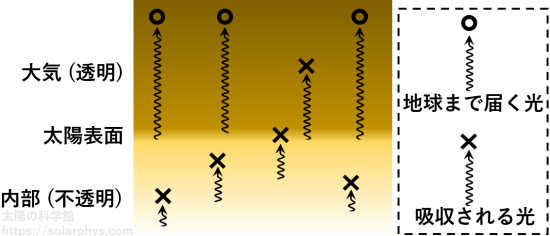
太陽大気は希薄なため、表面に比べると光子の放出反応が起きる頻度は僅かです。よって、地球で受け取る光子のほとんどは表面で生成されたものということになります。

図 26 に赤い実線で示した平均自由行程は、500 nm 付近の、かつどの原子種の励起・脱励起反応にも合致しない波長における \(\alpha\) のモデルから計算したものです。何らかの励起・脱励起反応が起きる波長の \(\alpha\) はずっと大きい値を取るので、その波長の光子の平均自由行程は図より小さくなります。よって、その波長で見たときには、「太陽表面」より高い層が表面として見えることになります ( 太陽表面の細かい定義について 脚注 [太陽表面の細かい定義]：表面として見える高度は、正確には見る光の波長によっても違いますし、円盤状に見える太陽の中心部分を見るか縁の付近を見るかによっても微妙に変わります。波長 500 nm の光 (連続光) で中心部を観測したときに光が発せられている面が高度ゼロと定義されることが多いです。光球は高度ゼロから 500 km 程度の層を指します。 )。この仕組みを用いることで、七変化の記事 で説明しているように、表面の上の 彩層 脚注 [彩層]：太陽大気のうち、高度 500 km から数千 km の層を指します (太陽半径は約 70 万 km)。太陽表面より少しだけ上の領域と考えてください。例えば波長 656.3 nm (Hα 線) や 396 nm (Ca H 線)、 30.4 nm の光などで観測すると見ることができます。 のような領域を観測することができます。詳しくは スペクトル線の記事 で説明します。

周縁減光

図 28 に、観測される太陽表面の様子 ( 図 1 ) を再掲します。円盤状に見える太陽表面の中心付近より、縁の付近の方が暗く見えています。この現象を「周縁減光 (limb darkening)」と言います。公開されている画像によっては、縁まで同じ明るさのものもありますが、そのような画像は人工的な処理によって周縁減光が取り除かれています。黒点のような構造をフラットに観察するためにそのような処理がなされることがあります。

周縁減光は幾何学的な理由によって起きます。円盤状に見える太陽の中心を観察した場合、太陽表面を鉛直に横切ってきた光線を観測することになります ( 図 29 A )。対して、縁付近を観測した場合は、斜めに横切った光線を見ます。この光線の鉛直からの角度を \(\theta\) とします。

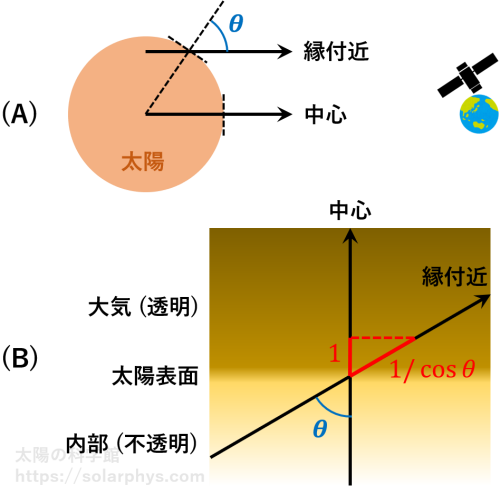
縁付近を観測したときの光線は、中心を観測したときの光線より、太陽表面付近の層を \(1/\cos\theta\) 倍だけ長い距離貫いています ( 図 29 B )。同じ吸収係数を持った層を長い距離進むということは、この光線に含まれる光子たちにとっての実効的な吸収係数は \(\alpha/\cos\theta\) の大きさになっていることになります。実効的な平均自由行程は \(\cos\theta (\lt 1)\) 倍と、小さくなるため、縁付近を観測した場合はその分だけ外側の層が表面として見えています。

太陽表面付近では、外側に行くほど温度が低くなっています。よって、縁付近を観測した場合は、より温度の低い層からの黒体放射を観測することになります。黒体放射は温度が低いほど暗いので、縁付近が暗く見えています。

この説明を逆手に取ると、周縁減光の具合を調べることによって、表面付近の温度の高度分布が分かります。

プランク関数の波長依存性

図 7 に示した様々な温度でのプランク関数の様子を 図 29 に再掲します。プランク関数はある波長にピークを持っていて、ピークより波長が短くなっても長くなっても値は減少します。ピークは温度が高くなる程短い波長側に移動します。これらの特徴の原因を説明します。

波長の短い側での挙動

光子の波長はエネルギーに反比例します。例えば波長 400 nm の光子が持つエネルギーは、波長 800 nm の光子が持つエネルギーの 2 倍です。具体的には、光子の持つエネルギー \(E\) は次のように書けます。

\begin{align} E &= \frac{hc}{\lambda} \\ \text{ただし}, \quad h &= 6.63 \times 10^{-34} \ \text{J s} \\ &: \text{プランク定数} \\ \quad c &= 3.00 \times 10^8 \ \text{m/s} \\ &: \text{光速} \\ \quad \lambda &: \text{その光子の波長 [m]} \end{align}

光子の吸収・放出反応では、反応前後で関係する物質粒子が得た (失った) エネルギー \(\delta E\) に相当する波長の光子が吸収 (放出) されます ( 図 31 )。エネルギー保存則からの帰結です。このエネルギー差 \(\delta E\) が大きい反応ほど、より波長の短い光子を吸収・放出するわけです。

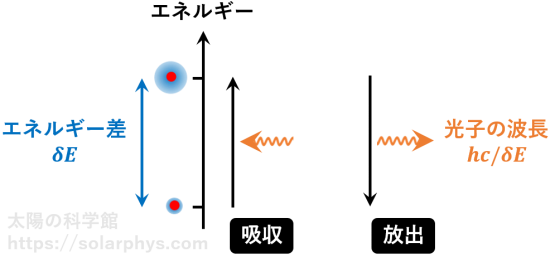
エネルギーの高い状態にある粒子の数密度 \(n^*\) と、低い状態にある粒子の数密度 \(n\) の比 \(n^*/n\) は、熱平衡では温度が与えられれば決定されると述べました。両状態のエネルギー差 \(\delta E\) が大きいほど、この比の値は小さくなります。具体的には、次の因子に比例します。

\begin{align} \frac{n^*}{n} &\propto \exp\left(-\frac{\delta E}{k_BT}\right) \tag{1}\\ \text{ただし},\quad k_B &= 1.38 \times 10^{-23} \ \text{J K}^{-1} \\ &: \text{ボルツマン定数} \\ T &: \text{物質の温度} \end{align}

\(\exp x\) とは \(e^x=(2.71\cdots)^x\) のことです。エネルギーの高い状態はより不安定なため、熱平衡ではより存在しにくいのです。

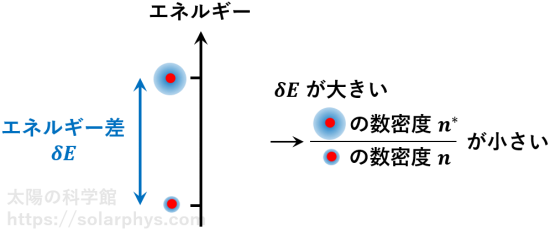
よって、熱平衡では、エネルギー差 \(\delta E\) の大きな反応 ( = 波長の短い光子を吸収・放出する反応) 程、

\[\frac{\varepsilon}{\alpha}=\frac{a}{b}\frac{n^*}{n}\]

の値は小さくなります。つまり、プランク関数 \(B_\lambda (T)\) の値は波長が短い側では小さくなります。

波長の長い側での挙動

プランク関数は波長の短い側だけでなく、長い側でもその値が小さくなっています。この原因はかなりややこしい話になりますが、量子力学的な理由です。

まず、上の節で説明を簡単にするために省いていた部分を正さねばなりません。光子の吸収や放射が起きる頻度の考察をしたときは、誘導放射を無視しました。誘導放射を考慮してもう一度考え直します ( 図 33 )。

誘導放射も光子との衝突によって起きる反応なので、光子の数密度に比例します。上の説明では、光子の数密度 \(n_\text{ph}\) は光線の強度 \(I\) に等しいと説明しましたが、正確には、強度とはある面を単位時間・単位面積あたりに通過するエネルギー量に相当する概念なので、注目する光線に属する光子の数密度 (正確には、ある面を単位時間・単位面積あたりに通過する光子数) \(n_\text{ph}\) に、注目する波長の光子が持つエネルギー \(hc/\lambda\) を乗じたものに比例します。

\[I \propto n_\text{ph}\cdot \frac{hc}{\lambda}\tag{2}\]

自発放射が起きた場合に、光子がどの方向に放出されるかはランダムです。今考えている「自発放射の起きる頻度」とは、厳密には注目している光線の方向に光子を放出するような自発放射が起きる頻度ということです。この頻度は光子の波長 \(\lambda\) に依存します。具体的には \(\lambda\) の 4 乗に反比例することを後から説明します。とりあえず受け入れてください。

\[a \propto \frac{1}{\lambda^4}\tag{3}\]

因みに、誘導放射は、衝突した光子の進行方向に新たな光子を 1 個加える反応です。よって、光線に属する光子との衝突による誘導放射では光線の方向に光子が放出され、属さない光子との衝突では異なる方向に放出されます。

数学的な便宜のため、誘導放射は常に「負の吸収」として考えられます。吸収が起きる頻度は、真の吸収と負の吸収による効果を合わせて、

\[\alpha I=bSnn_\text{ph}-cSn^*n_\text{ph}\tag{4}\]

と表されます。式 (1), (2), (3), (4), 図 31 の関係と 図 33 に記した自発放射の頻度を用いると、熱平衡における比 \(\varepsilon/\alpha\) は次の形に書けることが分かります。

\begin{align}\frac{\varepsilon}{\alpha} &= \frac{aSn^*\cdot I}{bSnn_\text{ph}-cSn^*n_\text{ph}} \\ &\propto \frac{1}{\lambda^5}\frac{1}{b'\exp[hc/(\lambda k_BT)]-c} \end{align}

しっかりと量子力学的考察を行うと、上式で導入した定数 \(b'\) と \(c\) は等しいことが分かります。結局のところ、次の形に書けます。

\[\frac{\varepsilon}{\alpha}\propto\frac{1}{\lambda^5}\frac{1}{\exp[hc/(\lambda k_BT)]-1}\]

これがプランク関数の厳密な波長依存性です。\(e^x-1\) が \(x\ll 1\) の場合には \(e^x-1\simeq x\) と近似できることを用いると、上式は \(\lambda\) が十分に大きい場合には減少関数になることが分かります。減少関数になるのは因子 \(1/\lambda^5\) の効果です。この因子は、\(I\) が \(1/\lambda\) に依存することと、自発放射の頻度が \(1/\lambda^4\) に依存することの帰結として出てきます。

自発放射の頻度についての補足

注目する光線の方向に光子を放出する自発放射が起きる頻度が、光子の波長 \(\lambda\) の 4 乗に反比例することを説明します。

今まで、ある特定の方向に向いた光線内の光子に注目して話を進めてきました。厳密に言うと、「特定の方向」の光線を考えることは物理的ではありません。光線に含まれる光子の数を議論するためには、特定の方向を含むある程度の 立体角 脚注 [立体角]：立体角とは、簡単にいうと、2 次元的な角度のことです。2 つの直線のなす角度 (単位：ラジアン [rad]) が \(\theta\) のとき、この直線が張る半径 1 の円弧の長さは \(\theta\) になるのでした。これに対応して、ある錐体のなす立体角 (単位：ステラジアン [sr]) が \(\Omega\) のとき、この錐体と半径 1 の球面との交線がつくる面積は \(\Omega\) になります。全方向を見込む立体角は \(4\pi\) であり、地平線より上にある部分 (全方向の半分) を見込む立体角は \(2\pi\) です。 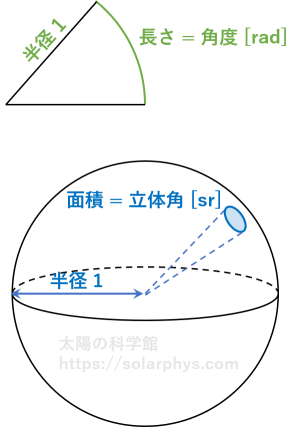\(d\Omega\) を持った方向に進む光子の集団を考えます。

更に、波長についても、ある特定の波長 \(\lambda_0\) の周りのある幅 \(d\lambda\) を持った波長域に属する光子の集団に注目します。また、その光子を放出し得る反応に注目します。

光子のエネルギーは先ほど述べたように \(hc/\lambda\) ですが、一方で光子の運動量 \(\vec{p}\) は、

\[\vec{p}=\frac{h}{\lambda}\vec{\ell}\]

と表されます。\(\vec{\ell}\) は光子の放射方向を向いた単位ベクトル (長さが 1 のベクトル) です。ただし、光子は光速で運動する粒子なので、運動量と速度の \(\vec{p}=m\vec{v}\) という関係は成り立っていないことには留意してください (光子の質量はゼロです、この記事の説明ではあまり気にしないでください)。

注目している自発放射が起きると、上式より定まる特定の運動量 \(p_0=h/\lambda_0\) を含むある幅 \(dp\) 以内の大きさの運動量を持った光子が放出されます。しかし、その放射方向 \(\vec{\ell}\) は原子が特殊な状況に置かれていない限り、ランダムに決まります。

量子力学によると、粒子の運動量は「離散的な値」をとります。これは次のイメージです。光子の運動量 \(\vec{p}\) の \(x, y, z\) 成分 \(p_x, p_y, p_z\) を軸にとった 3 次元的なグラフ (運動量空間) を描きます ( 図 34 )。例えば光子が \((p_x,p_y,p_z)=(1,2,3)\) という値の運動量を持っていたならば、このグラフ上では 1 点で表せます。

このとき、光子はこの運動量空間中の全ての点に対応する運動量の値を持つことができるわけではありません。実際には、図に青色で示したように、格子点に対応する運動量の値しかとり得ません。

たくさんある格子点のうち、特定の点に対応する運動量を持つ光子を放出する自発放射が起きる頻度は、上の節でも出てくる線強度 \(S\) に比例します。そして、各格子点の運動量を持つ光子が、その大きさが \(p_0\) 付近であるという条件を満たす限りにおいて、同様に確からしく放射されます。

つまり、注目する光線に属する光子を放出する自発放射が起きる頻度 \(\varepsilon\) は、次の量に比例します。

\[\varepsilon \propto n^*S\cdot (\text{格子点の数})\]

一般に、隣接する格子点間の距離より十分に大きい領域を考える場合、その領域に含まれる格子点の数は領域の体積に比例します。注目している光線に属する光子は、運動量空間中の 図 35 に青色で示した球殻片に対応する運動量を持ちます。

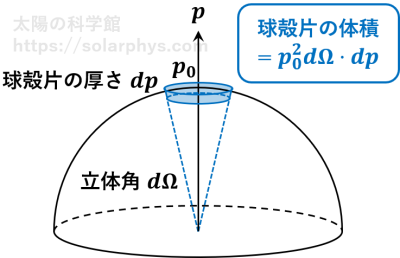
この球殻片の体積は \(p_0^2dp\) に比例します。よって、

\[\varepsilon \propto n^*Sp^2dp\]

と書けることが分かります。\(dp\) と \(d\lambda\) の間には次の関係があります。

\[dp = d\left(\frac{h}{\lambda}\right)=-\frac{h}{\lambda^2}d\lambda\]

光子の運動量の大きさが波長に反比例することを考慮すれば、結局次のように、\(\varepsilon\) は波長の 4 乗に反比例します。

\[\varepsilon\propto \frac{n^*S}{\lambda^4}\]

以上のことをまとめると、波長の長い側でプランク関数の値が減少する理由は、次の 2 つということになります。

• 波長の長い光子が持つエネルギーは小さいため、仮に同じ数だけの光子が光線に属していたとしても、波長が長いほど光線の強度 \(I\) が小さくなる。
• 放出される光子が持ち得る運動量のバリエーション数が、特定の光線に注目する限り、波長の 4 乗に反比例して少なくなる。よって、確率論的な帰結として、波長が長いほど注目する光線に光子が放出される頻度が少ない。

参考文献

記事全体として参考にした書籍

• Castor, J. (2004). Radiation Hydrodynamics (Cambridge: Cambridge University Press ).
• Rybicki, G. B. and Lightman, A. P. (1985). Radiative Processes in Astrophysics (Weinheim: Wiley-VCH ).

引用した文献

• Adelman, S. J. (2004). The physical properties of normal A stars. Proceedings of the International Astronomical Union, 2004 (IAUS224), 1-11 .
• Christensen-Dalsgaard, J., Däppen, W., Ajukov, S. V., Anderson, E. R., Antia, H. M., Basu, S., Baturin, V. A., Berthomieu, G., Chaboyer, B., Chitre, S. M., Cox, A. N., Demarque, P., Donatowicz, J., Dziembowski, W. A., Gabriel, M., Gough, D. O., Guenther, D. B., Guzik, J. A., Harvey, J. W., Hill, F., Houdek, G., Iglesias, C. A., Kosovichev, A. G., Leibacher, J. W., Morel, P., Proffitt, C. R., Provost, J., Reiter, J., Rhodes Jr., E. J., Rogers, F. J., Roxburgh, I. W., Thompson, M. J. and Ulrich, R. K. (1996). The current state of solar modeling. Science, 272, 1286-1292 .
• Dolan, M. M., Mathews, G. J., Lam, D. D., Lan, N. Q., Herczeg, G. J., and Dearborn, D. S. P. (2016). Evolutionary tracks for Betelgeuse. The Astrophysical Journal, 819, 7 .
• Kervella, P., Decin, L., Richards, A. M. S., Harper, G. M., McDonald, I., O’Gorman, E., Montargès, M., Homan, W. and Ohnaka, K. (2018). The close circumstellar environment of Betelgeuse. V. Rotation velocity and molecular envelope properties from ALMA. Astronomy & Astrophysics, 609, A67 .
• Liebert, J, Young, P. A., Arnett, D., Holberg, J. B. and Williams, K. A. (2005). The age and progenitor mass of Sirius B. The Astrophysical Journal Letters, 630, L69-L72 .
• Moravveji, E., Guinan, E. F., Shultz, M., Williamson, M. H. and Moya, A. (2012). Asteroseismology of the nearby SN-II progenitor: Rigel. I. The MOST high-precision photometry and radial velocity monitoring. The Astrophysical Journal, 747, 108 .
• Peterson, D. M., Hummel, C. A., Pauls, T. A., Armstrong, J. T., Benson, J. A., Gilbreath, G. C., Hindsley, R. B., Hutter, D. J., Johnston, K. J., Mozurkewich, D. and Schmitt, H. (2006). Resolving the effects of rotation in Altair with long-baseline interferometry. The Astrophysical Journal, 636, 1087-1097 .
• Schiller, F. and Przybilla, N. (2008). Quantitative spectroscopy of Deneb. Astronomy & Astrophysics, 479, 849-858 .
• Tkachenko, A., Matthews, J. M., Aerts, C., Pavlovski, K., Pápics, P. I., Zwintz, K., Cameron, C., Walker, G. A. H., Kuschnig, R., Degroote, P., Debosscher, J., Moravveji, E., Kolbas, V., Guenther, D. B., Moffat, A. F. J., Rowe, J. F, Rucinski, S. M., Sasselov, D and Weiss, W. W. (2016). Stellar modelling of Spica, a high-mass spectroscopic binary with a β Cep variable primary component. Monthly Notices of the Royal Astronomical Society, 458, 1964-1976 .
• Vernazza, J. E., Avrett, E. H. and Loeser, R. (1981). Structure of the solar chromosphere. III. Models of the EUV brightness components of the quiet Sun. The Astrophysical Journal Supplement Series, 45, 635-725 .
• Yoon, J., Peterson, D. M., Kurucz, R. L. and Zagarello, R. J. (2010). A new view of Vega's composition, mass, and age. The Astrophysical Journal, 708, 71-79 .