統計を取ると現れる謎の周期
図 1 は国立天文台三鷹にある望遠鏡が 2000 年 1 月 15 日に捉えた太陽表面です。たくさんの黒い点模様が映っています。黒点と呼ばれます。黒点について詳しくは記事「黒点：磁場が通り抜ける「穴」」で説明しています。図に映っている黒点は大きいものから小さいものまで様々です。黒点の数は日によって変化します。国立天文台の記録によると、この日の黒点数は 45 個とカウントされています。
一方で、図 2 は 2009 年 1 月 15 日の太陽表面です。こちらの画像では、黒点はひとつも確認できません。国立天文台の記録でも、この日は黒点がゼロであるとカウントされています。
図 3 は 図 1 と 図 2 が撮られた日を含む、2000 年 1 月および 2009 年 1 月の黒点数の日ごとの変化を表しています。日ごとにばらつきはありますが、2000 年に比べて、 2009 年の黒点数は統計的に少ないことが見てとれます。
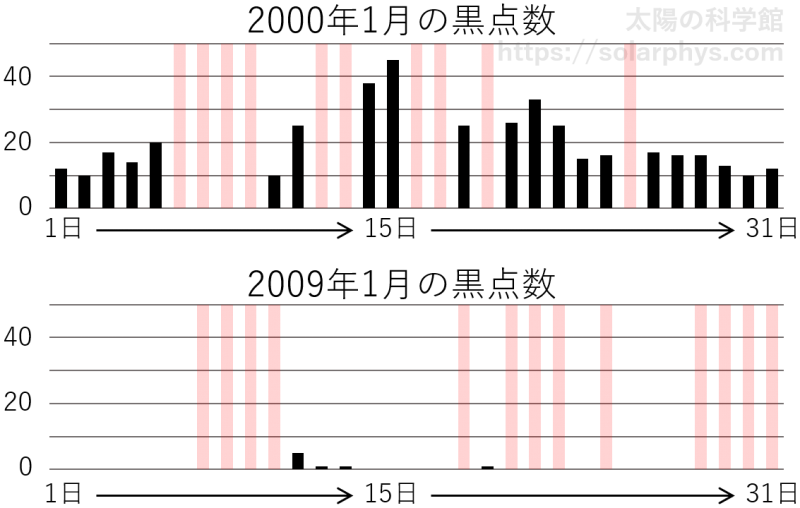
図 4 の下段に注目してください。これは地球から見える太陽表面の何 % の面積を黒点が占めているかを縦軸として表したものです。横軸は時間で、1870 年代から 2015 年までの観測データがずらっと並んでいます。黒点数が増えれば自ずと黒点面積も増えるため、先ほど示した黒点数と大体同じような指標と思っていただければ結構です。
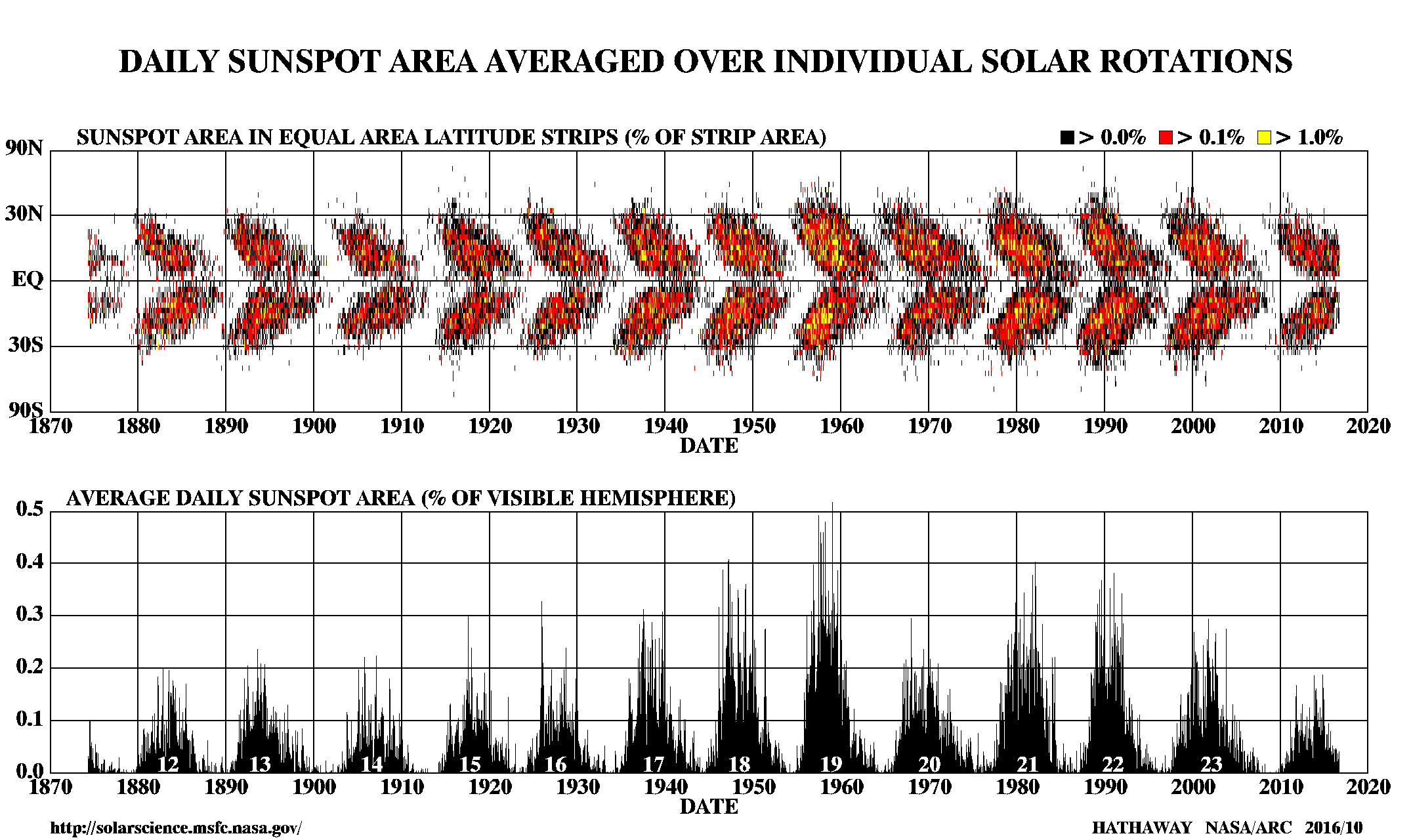
図を見ると、規則的に黒点面積が増えたり減ったりしていることが目に付くと思います。この周期は平均すると 11 年になります。サイクルによっては 10 年だったりと、多少のばらつきはありますが、かなり綺麗な周期性を持っています。
詳しくは記事「活動領域：フレアの量産源」で説明していますが、黒点の上空の
コロナ
脚注
[コロナ]：高度数千 km より高層の大気を指します (太陽半径は約 70 万 km)。極端紫外線や X 線で見ることができます。
では爆発現象「フレア」が頻繁に発生します。このフレアで吹き飛ばされた物質が地球を直撃すると、通信や電気インフラに被害を及ぼすことがあります。黒点が多い時期には自ずとフレア数も多くなり、黒点が少なくなるとフレア数も少なくなります。このような事情から、図の 11 年周期の中で黒点面積が大きくなる時期を「太陽活動の極大期」、逆に面積が小さく (ほぼゼロに) なる時期を「極小期」と呼びます。
極小期から次の極小期までを 1 つの太陽周期と言うことがあります。図 4 をよく見ると、白い数字が各周期に振られていることが分かると思います。このように、各周期には名前 (番号) がついています。2020 年現在は第 24 周期と来る第 25 周期の間の極小期であり、第 25 周期の黒点が時々出現するようになってきたところです。
図 5 は 図 1 に赤道と北緯/南緯 30 度の線を書き込んだものです。図を見ると、黒点は大体 緯度 30 度より赤道側にできていることが分かります。このように、黒点にはできやすい緯度があり、そのような緯度は 11 年周期の中で変化していきます。その様子を示したものが 図 6 の上段です。図 4 を再び載せています。
図の上段のグラフは縦軸が緯度を表しており、各緯度ごとに、面積にしてどのくらい黒点が存在していたかが色で表されています。
図を見ると、規則的な繰り返しのパターンが確認できます。11 年周期の始まり (極小期の直後) では比較的高緯度に黒点が現れやすく、その緯度は周期が進行すると共に赤道に近づいていきます。その後、極小期が訪れ、再び高緯度を中心に黒点が出現し始めます。黒点の現れる緯度は多少の例外はあるものの、およそ緯度 30 度以内です。この図は蝶の羽がいくつも並んでいるように見えるので、蝶形図 (butterfly diagram) と呼ばれます。
このように、黒点について、何十年にもわたって統計を取ると、驚くほど綺麗な規則性が現れます。この周期性はなぜ生まれるのか？ 11 年という数字を決めているのは何なのか？という疑問は、このページの下の方で説明するように、太陽の磁場がどのようにして生成され維持されているのか？という疑問とも深い関係にあります。これらは太陽物理において、未だに世界中の研究者の間で一致した回答が得られていない大問題のひとつです。
秩序立った磁場の振る舞い
図 7 は第 22 周期と第 23 周期のとある日の太陽表面です。色は太陽表面の磁場の様子を表しています。黄色は
磁力線
脚注
[磁力線]：各場所での磁場の向きを繋げた曲線を磁力線と言います。理想的には磁力線の密集度がその場所での磁場の強さ (単位 T, テスラ) を表しますが、実際の図では特徴的な磁力線だけを間引いて描くため、この限りではありません。磁力線が分裂したり合流したりすることはありません。電気を通すプラズマでは磁力線は物質に凍結している (物質は磁力線に垂直な方向に動くことができない) ので、磁力線の動きはその場所でのプラズマ (物質) の動きを表します。
が太陽内部から大気へ向かって突き出している領域を表し、青色は逆に、大気から内部に向かって突き刺さっている領域を表しています。グレーは磁場が弱い領域です。どのようにして磁場の様子を知ることができるのかについては、記事「プラズマ診断：太陽を「見る」だけでここまで分かる」で説明しています。
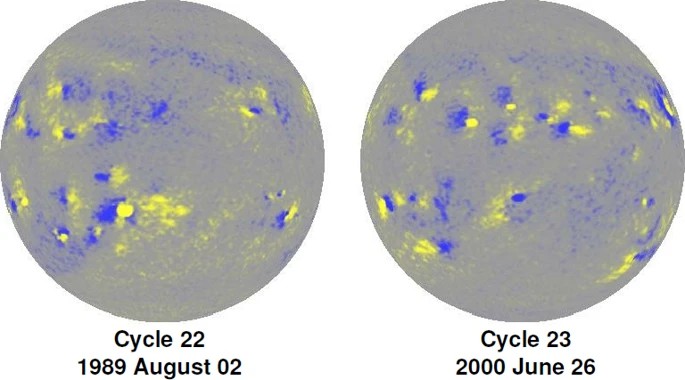
図 7 に示された表面磁場の構造を模式的に表したものを 図 8 に示します。図のように、表面磁場は黄色と青色の対がたくさん寄せ集まった構造をしていると解釈できます。太陽は図の右向きに自転していることを考慮して、この対構造の内の右側を先行磁極、左側を後続磁極と呼ぶことにします。典型的にはこの対構造の部分が黒点になります。両磁極に黒点が形成されて対の状態で存在することもありますし、先行磁極のみに形成されて単体で存在することもあります。詳しくは活動領域の記事も読んでください。
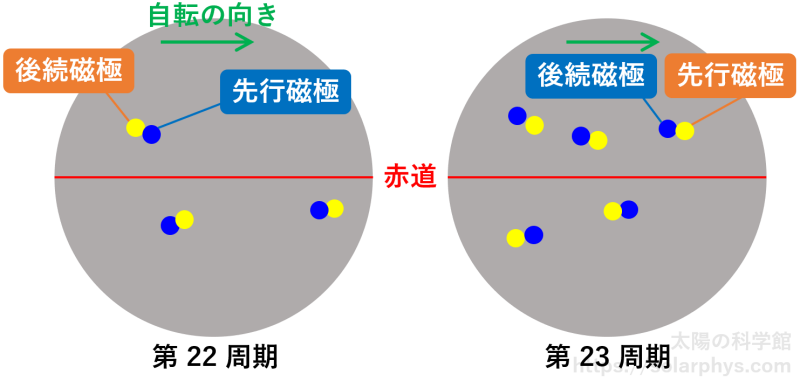
先行磁極の極性に注目してください。第 22 周期では北半球の先行磁極は青色、南半球の先行磁極は黄色になっていることが分かると思います。対して、第 23 周期では北半球が黄色、南半球が青色になっています。中にはイレギュラーな対構造もありますが、ほとんどがそうなっています。整理すると、
- 北半球と南半球では先行磁極の極性が逆である
- そしてその極性は次の太陽周期では反転する
ということが言えます。これはヘール-ニコルソンの法則と呼ばれます。
図 8 では、恣意的に対構造を赤道に対して傾けて (非平行に) 描きました。実は、この傾きについての法則も統計的に示されています。図 9 は第 23 周期に観測された活動領域 (黒点) の傾き角 (定義は図のキャプションを参照) と緯度の分布を示したものです。北半球では平均的に傾き角が正で、南半球では反対に負であることが読み取れます。これは、北半球でも南半球でも、先行磁極が後続磁極より赤道に近いことを示します。これをジョイの法則と言います。ただし、あくまでも平均を取ったときの話であり、図を見るとこの法則に従わない黒点もあることが分かります。
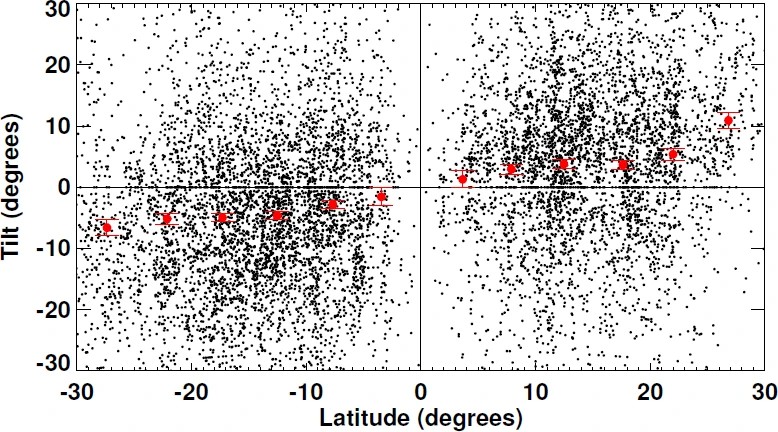
図 10 では、表面磁場を各緯度ごとに
経度方向
脚注
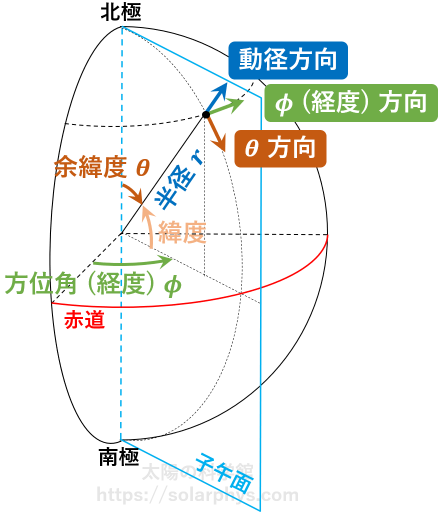
[極座標]：半径 \(r\)、余緯度 \(\theta\)、方位角 \(\phi\) の 3 つの値で点を指定する方法を極座標 (球座標) と言います。太陽は大雑把に球対称の天体なので、極座標がよく用いられます。方位角は経度とも言います。余緯度は北極から測った角度ですが、代わりに赤道から測った角度である緯度が用いられることもあります。球を縦に (北極と南極を通るように) 切った平面を子午面と言います。
に渡って平均した値が色で示されています。縦軸は緯度、横軸は時間を表しています。ボタンを押すと説明の有無を切り替えられます。
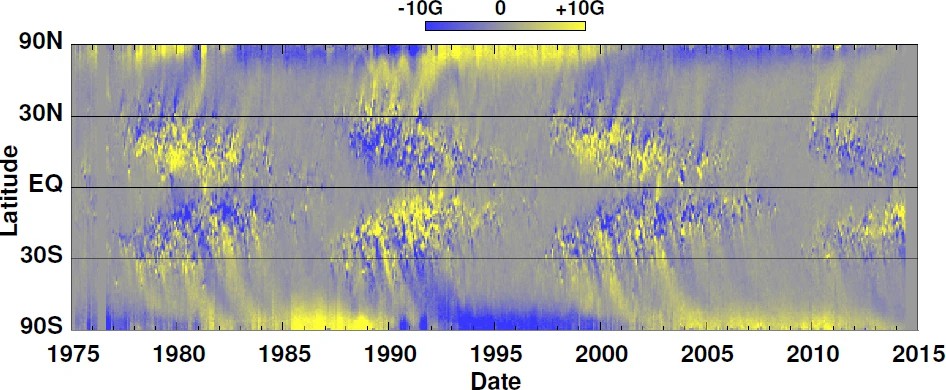
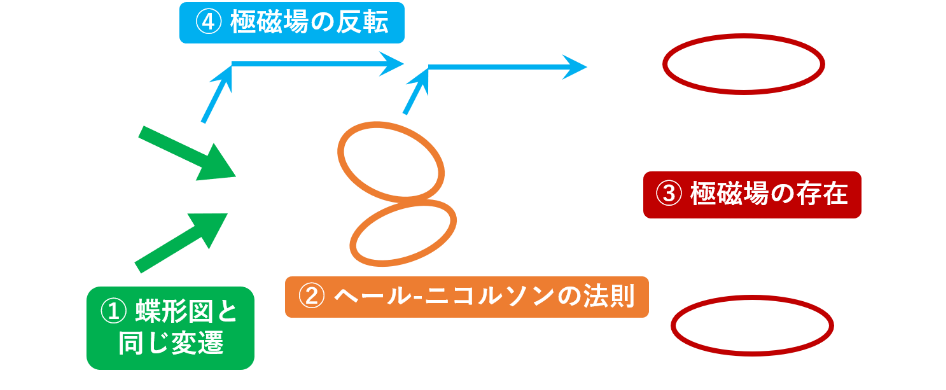
図を見ると、次の 4 つの特徴が確認できます。図の下段にそれぞれ示しています。
- 緯度 30 度以内の部分では、黒点の存在によって平均磁場が強い。このことが蝶形図と同じパターンとして表れている。
- その蝶形の色に注目すると、北半球と南半球では逆であり、次の周期では反転するという、ヘール-ニコルソンの法則を再現している。平均すると、先行磁極の極性が後続磁極の極性に打ち勝つようである。
- 極域にも磁場が比較的強い領域が見られる。その極性は北極と南極では逆である。黒点の磁場の強さは典型的には \(0.3 \ \text{T}\) (
テスラ
脚注
[テスラ]：磁場の強さを表す単位です。理想的には磁力線の密集度に相当しますが、実際の図では特徴的な磁力線だけを間引いて描くため、この限りではありません。磁場の強さの単位には \(\text{G}\) (ガウス) が使われることもあり、\(1 \ \text{G}=10^{-4} \ \text{T}\) です。
) 程度であるのに比べて、極域磁場の強さは \(10^{-4} - 10^{-3} \ \text{T}\) 程度であることが観測から分かっている。
- 極域磁場は太陽周期の途中、極大期付近で、先行磁極の極性から後続磁極の極性に反転する。黒点形成領域から極域に磁場が運ばれているような模様も見え、この運ばれた磁場が極域磁場の反転を促しているようにも見える。
このように、表面磁場の観点から周期性を調べると、黒点の蝶形図と極域磁場が連動して 1 つのパターンを描いていることが分かります。磁場の極性まで考慮に入れると、その周期は通常の意味での「太陽周期」の 2 つ分、つまり 22 年です。ここまで来ると、 11 年周期問題は、秩序立った磁場極性の挙動をどのように説明するかという問題であることが見えてきます。
磁場生成のおおまかな仕組み
黒点の 11 年周期は問題の一側面を見ているだけであって、問題の本質は太陽表面の磁場が 22 年ごとに繰り返すパターンを説明することであると上の節で説明しました。これは、太陽表面で観測される磁場がどのように維持されているのかという問題でもあります。この問題に対して自信を持って具体的なシナリオを説明することはまだできません。しかし、磁場を生成、維持する仕組みは、おおまかには次のようなものであろうと考えられます。
まず最初に、太陽の磁場は磁石とは違う仕組みで維持されています。磁石はたくさんの原子が集まってできており、更にそれらの原子は原子核と電子から構成されます。磁石が帯びている磁気の源は、原子内の電子が回転運動をすることで発生する磁場です。通常の物質では、この回転運動の向きは各原子で勝手な方向を向いているので、発生した磁場は周りの原子同士で打ち消し合って、物体全体としては磁気を帯びません。しかし、磁石の材料となる物質は、回転運動の向きが各原子で揃っている方が安定するという性質を持つため、「塵も積もれば山となる」の結果、磁石全体として磁気を帯びることになります。太陽は熱い気体であり、このような性質は持ちません。
太陽は主に水素とヘリウムから成る気体です。ただし、例えば地球大気のような気体とは違って、電気を非常に通しやすいという特徴を持ちます。別の言い方をすると、電気抵抗が物凄く小さいということです。そのような気体は
プラズマ
脚注
[プラズマ]：粒子が電子を手放して電荷を持つようになることを電離と言います。太陽内部やコロナは温度が高いので、主な構成元素である水素やヘリウムは、電離してイオンの状態で存在します。電荷を持った粒子を含む気体をプラズマと言います。太陽表面は温度が不十分なので、一部の粒子のみが電離しています。この状態を部分電離と言います。
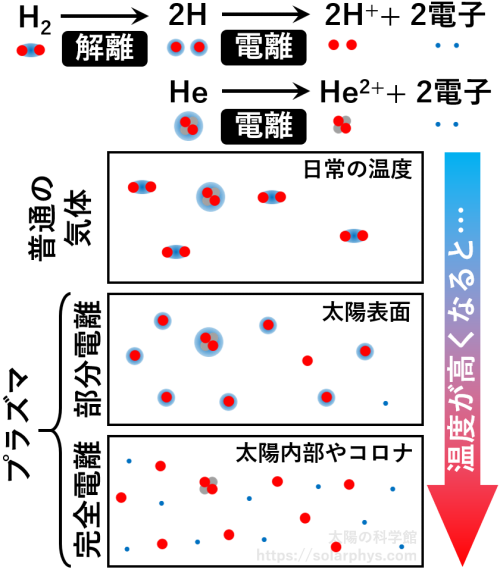と呼ばれることがあります。詳しくは記事「プラズマとは何か？：宇宙の基本要素」で説明しています。この電気伝導性が太陽磁場の起因を語る上でいちばん重要な性質です。
記事「プラズマと磁場：磁力線が「実体」を帯びる」で説明していますが、プラズマが電気を非常に通しやすいことの帰結として、磁力線はプラズマに対して相対的に動くことができないという性質を持ちます。太陽内部では、プラズマが動くと、それに伴って磁力線も共に動かなければなりません。まるで磁力線がプラズマに対して「凍結」しているかのように振舞うわけです。
太陽の内部では様々な種類の流れが存在します。このプラズマの流れによって磁力線が揉まれ、引き伸ばされたりねじられたりする過程で増幅することにより、太陽は磁場を維持し続けています。このことをエネルギーの観点で説明すると 図 11 のようになります。
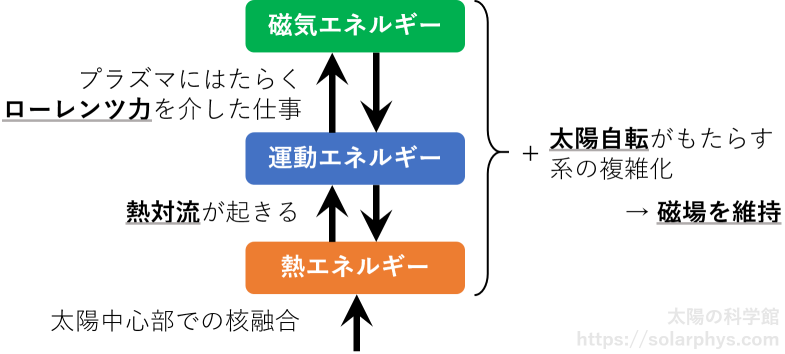
太陽中心部では核融合が起きており、それによって発生する熱が常に外側へ運ばれてきます。この熱の流れによって、太陽内部のうちの外側の部分は
熱対流
脚注
[熱対流]：水の入った鍋を下からコンロで熱すると、熱くなった底付近の水は軽くなって上方へ移動します。逆に元々鍋の上方にあった水は熱せられた水と比べて重いため、下方へ移動します。これの繰り返しによって、鍋の中の水は温度を一様にしようとします。これが熱対流です。エネルギーの観点では、下からコンロによって加えられる熱エネルギーを熱対流が上方へ輸送していることになります。
をしています。記事「基本構造：何からできているのか？」で説明している
対流層
脚注
[対流層]：太陽半径を \(R_\odot =\) 約 70 万 km としたとき、\(0.7 R_\odot \)から表面 (\(1 R_\odot\)) までの領域を指します。この領域では主に熱対流によってエネルギーが外側へと運ばれます。
のことです。更に、太陽は自転をしており、その影響で対流層には複雑な流れが存在しています。
磁場の中をプラズマが流れると電流が発生します。いわゆる電磁誘導です。電流と磁場が存在すると、プラズマは
ローレンツ力
脚注
[ローレンツ力]：電荷を持った粒子が磁場の中を運動をすると図の向きにローレンツ力を受けます。太陽を構成するプラズマ ( = 電気を通しやすい気体) は荷電粒子の集団であるため、電流 ( = 陽イオンと電子の間の相対的な動き) が発生すると各粒子にはたらくローレンツ力の合計としての力を受けることになります。単位体積あたりにはたらくローレンツ力 (単位 \(\text{N/m}^3\)) は電流 (単位 \(\text{A/m}^2\)) と磁場 (単位 \(\text{T}\)) の外積になります。
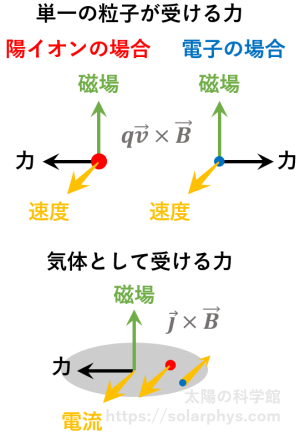を受けます。学校では「フレミングの左手の法則」で習う力です。この力によってプラズマが減速した場合、その分の運動エネルギーは磁場のエネルギーに変換されたことになります。このようなエネルギー変換の流れが太陽磁場の起源です。
では、例えば実験室で、電気を通す液体金属を熱して対流を起こさせ、種となる磁場を与えると、その後磁場を維持し続けるのかと問われると、そうではありません。太陽の場合、ここでも自転が重要な役割を担っています。自転によって起きる様々な現象が上手くかみ合って機能することによって、太陽は磁場を維持できるのです。ただし、後に述べるように、その「自転がもたらす現象」のうちのどれが磁場の維持に決定的な役割を果たしているのかがまだよく分かっていません。
このように、電気伝導性を持つ流体の流れによって磁場が維持される機構のことをダイナモ機構 (dynamo) と呼ぶことがあります。詳細は分からずとも、太陽の磁場がこのダイナモ機構によって維持されていることは、ほとんどの研究者が疑わないでしょう。地磁気もダイナモ機構によって維持されていると考えられています。地球の外核は液体の金属 (主に鉄とニッケル) でできており、やはり対流していると考えられています。そこに地球の自転の効果が加わって、地磁気を維持しているのだろうという説が有力です。太陽や地球に限らず、太陽系の天体だと水星、木星、ガニメデ (木星の衛星)、土星、天王星、海王星もダイナモ機構によって磁場を維持していると考えられています (例えば Stevenson, 2010 を読んでください)。また、夜空に輝く様々な天体で起こる現象を説明しようとすると、しばしば磁場が重要な役割を演じます。これらのそれぞれの天体に対してダイナモ機構の研究が行われています。
問題の整理
上述した磁場のパターンを説明するモデルの候補として、現在様々な機構が考えられています。観測事実が太陽周期モデルに与える制限をもう一度整理すると、次のようになります。
- 11 年 (22 年) で周期的な変化を起こすこと
- 黒点形成領域が赤道に向かって移動すること
- 北半球と南半球では極性が逆であること
- 極大期付近で極域磁場が反転すること
- 磁場の強さが観測と一致すること (黒点は \(0.1 \ \text{T}\)、極域磁場は \(10^{-3} \ \text{T}\) 程度)
これらの特徴を、太陽内部にあるプラズマの流れによって実現しなくてはなりません。太陽内部には次の 3 種類の流れが存在することが分かっています。
1 つ目は熱対流 (thermal convection) です。記事「粒状斑：太陽表面での対流」で説明しているように、太陽表面での熱対流は味噌汁で見られる模様のような粒状斑として観測されます ( 図 12 参照 )。この熱対流は太陽半径を \(R_\odot\) として半径 \(0.7 R_\odot\) の深さまで存在していると考えられています。この対流層と呼ばれる領域では、大小さまざまな渦が存在して、プラズマがごちゃごちゃにかき混ぜられている状態です。そのような乱雑な動きの状態を「乱流 (turblence)」と言います。
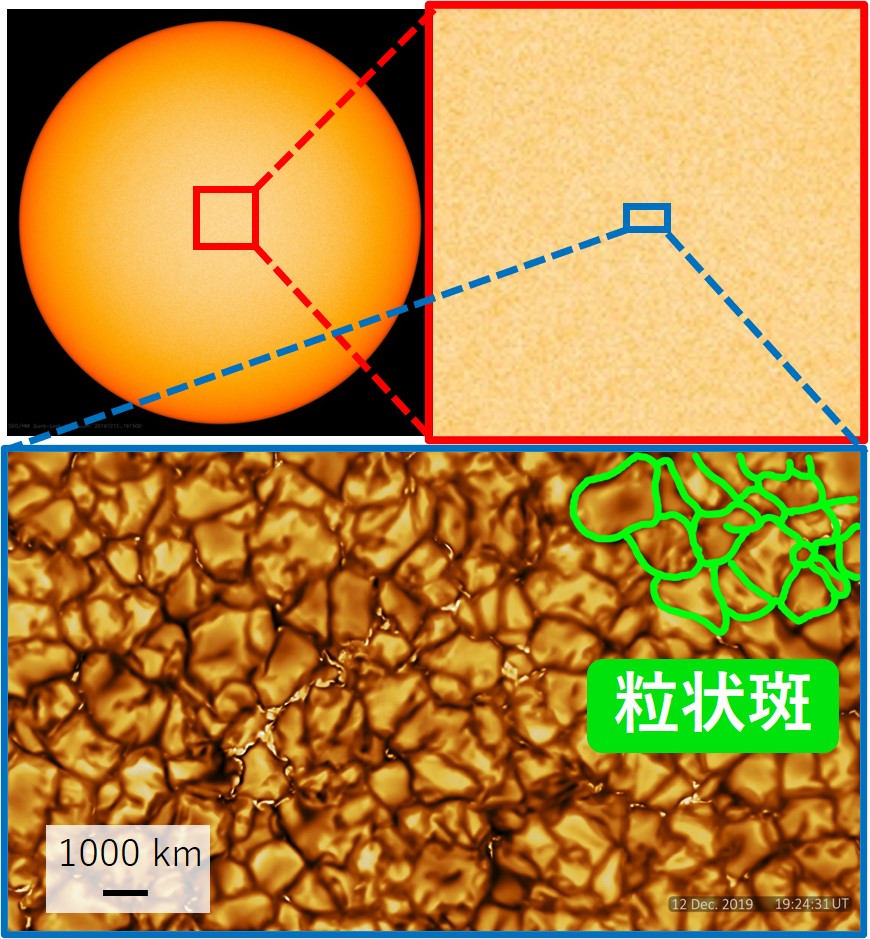
粒状斑 (表面での対流) の大きさは典型的には \(1000 \ \text{km}\) 程度であり、プラズマの流速は \(1 \ \text{km s}^{-1}\) 程度であることが分かっています。これに対し、対流層内部の対流はもっと大きく (1 万 \(\text{km}\) とか 10 万 \(\text{km}\) の桁数)、もっと遅い (10 \(\text{m s}^{-1}\) とか \(100 \ \text{m s}^{-1}\) の桁数) だろうと考えられています。参考として、太陽半径は 約 70 万 \(\text{km}\) です。
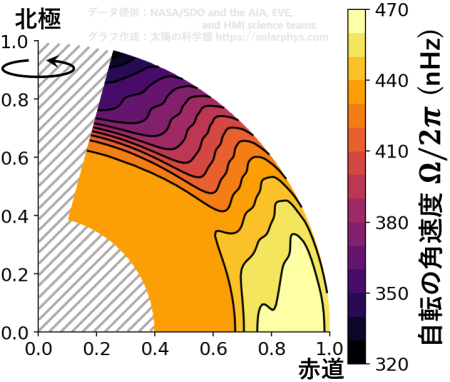
2 つ目は差動回転 (differential rotation) と呼ばれる流れです。記事「差動回転：回り方がおかしい？」で説明していますが、太陽は極よりも赤道の方が速く自転しています。記事「太陽内部を探る日震学」で説明している 日震学 脚注 [日震学]：太陽表面で観測される気体の振動や波を解析することで、太陽内部の圧力や密度、流れの様子などを知ることができます。この手法を日震学と言います。日震学はこれまで、太陽内部の理論モデル (標準太陽モデル) の観測的裏付けを与えた他、太陽内部の自転 (差動回転) の様子も明らかにしました。 によって、太陽内部は 図 13 のように回転していることが明らかになっています。図の読み方についてはキャプションを見てください。
3 つ目は子午面環流 (meridional circulation) と呼ばれる流れです ( 図 14 参照 )。これは、乱流状態にある対流層の動きを
経度方向
脚注
[極座標]：半径 \(r\)、余緯度 \(\theta\)、方位角 \(\phi\) の 3 つの値で点を指定する方法を極座標 (球座標) と言います。太陽は大雑把に球対称の天体なので、極座標がよく用いられます。方位角は経度とも言います。余緯度は北極から測った角度ですが、代わりに赤道から測った角度である緯度が用いられることもあります。球を縦に (北極と南極を通るように) 切った平面を子午面と言います。
に平均して、長い目で見ると浮き彫りになってくる弱い流れです。Gizon et al. (2020) の推定結果によると、緯度 30 度に注目したとき、太陽表面 (\(R_\odot\)) では \(10 \ \text{m s}^{-1}\) 程度の極向きの流れ、\(0.72 R_\odot\) の深さでは数 \(\text{m s}^{-1}\) 程度の赤道向きの流れが存在します。
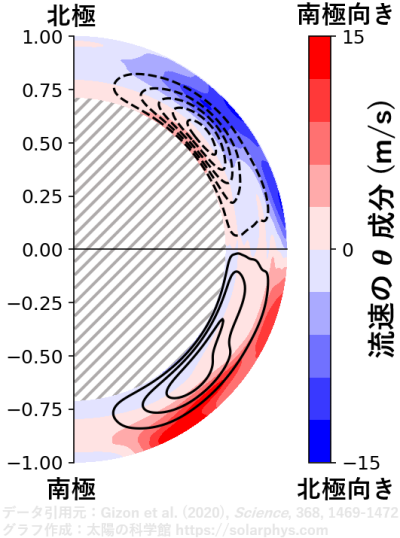
(球座標、\(r, \theta, \phi\)) で考えたときの、流速の \(\theta\) 成分を表す。第 24 太陽周期での平均。Gizon et al. (2020) のデータを基に作成。
子午面環流の推定も日震学によってなされますが、差動回転とは異なり、用いる観測データや推定方法に結果が大きく依存してしまいます。しかも、なぜ異なる結果が導かれるのか、未だに原因特定に至っていないのが現状です。よって 図 14 の結果も可能性のひとつとして見た方が良いかもしれません。上述した研究結果では北半球と南半球に 1 つずつ大きな環流が存在していますが、複数の環流に分かれていることを示唆するような研究結果も存在します。このことについては 差動回転の記事 でも説明しています。
これらの 3 種類の流れから、上述した制約を満たす磁場のパターンを作り出すようなモデルを完成させることが、太陽周期問題の目標です。
ダイナモ機構
分かってきた 3 つのピース
まずは、太陽周期のモデルを完成させるためのパズルのピースとして、実際に太陽で機能していそうだと考えられている 3 つの機構から説明します。
1 つ目は Ω (オメガ) 効果と呼ばれる機構です。仮に、 図 15 の左上のような磁力線が対流層に存在しているとします。上述したように、太陽は差動回転をしているため、この磁力線は太陽の自転と共に、図のように引き伸ばされるはずです。最終的には対流層に水平に横たわった、自転軸を取り巻くような向きの磁場が生成されます (図の右下)。このような磁場をトロイダル場と呼びます。
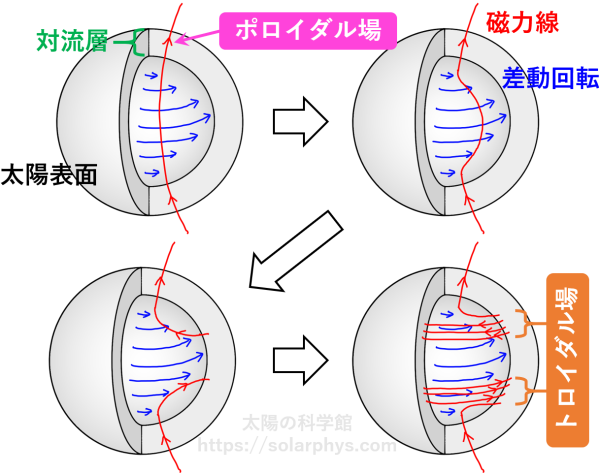
差動回転の分布 ( 図 13 ) を見ると、対流層の大部分には緯度方向の速度ずれ ( 図 16 の青色) があり、対流層の底には鉛直方向の強い速度ずれ (図の赤色、速度勾配層、tachocline) が存在します。図 15 は緯度方向の速度ずれによってトロイダル場が生成されることを想定して描きましたが、速度勾配層によって生成されている可能性もあります。また、初めの磁力線が 図 15 に描いたような形状ではなかったとしても、とにかく鉛直方向や極方向の磁場 (そのような磁場をトロイダル場に対してポロイダル場と言います) が存在すれば、差動回転による Ω 効果が起こります。その結果、対流層の底付近には強いトロイダル場が横たわっていると考えられています。
2 つ目のピースは磁束管の浮上と言われる現象です。これについては活動領域の記事で詳しく説明しています。対流層の底に強いトロイダル場が存在すると、その磁力線の一部が浮力を得て、表面まで上昇してくることがあります ( 図 17 参照 )。この浮上した磁力線の束が表面を突き抜けて大気に顔を出した場所が活動領域と呼ばれ、そのふもとの表面に黒点が形成されます。磁力線は途切れてはいけないので、大気に突き出した場所があれば、必ず再び潜っている場所もあります。このようにして、図 7 で見たような対の表面磁場構造ができるわけです。
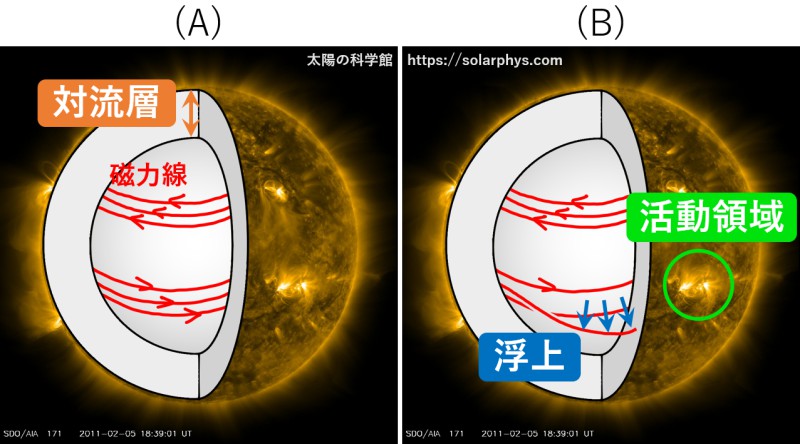
3 つ目のピースはバブコック-レイトン機構と呼ばれ、極域磁場の反転を説明するものです。ジョイの法則として上述したように、表面に現れる磁場の対構造は、先行磁極が赤道に近くなるように傾きがちなのでした。これは、磁力線が浮上する過程で
コリオリの力
脚注
[コリオリの力]：地球や太陽のような回転 (自転) する系の中で物質が速度を持つと受ける見かけの上の力 (慣性力) のことを言います。地球の外 (慣性系) から見ると等速直線運動をしている物体でも、回転する地球に固定された観測者 (回転系) からは軌道が曲がって見えます。これは回転系で考える場合には、「遠心力」「コリオリの力」の 2 つの慣性力を物体が受けていると解釈すれば辻褄が合います。遠心力は物体の運動に依らず外向きに働く力であり、コリオリの力は物体が回転系で見て動いている場合に遠心力に加えて働く力です。自転軸に沿って南極から北極を見た向きを \(\vec{\Omega}\)、回転系で見た物体の速度を \(\vec{v}\) としたとき、コリオリの力は外積 \(\vec{v}\times\vec{\Omega}\) の向きに働きます。
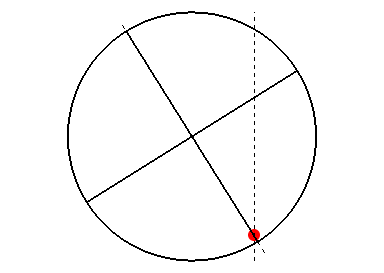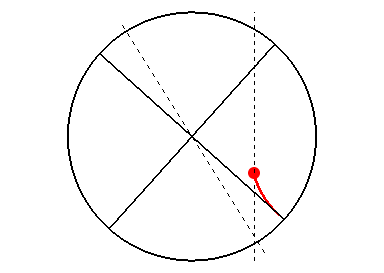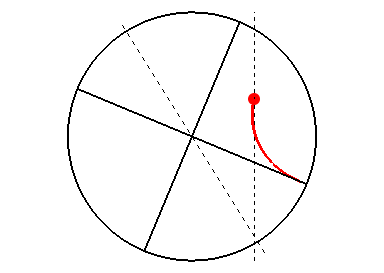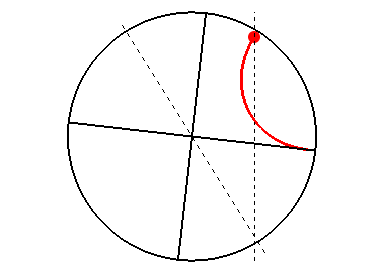の作用を受けるためであると考えられています。
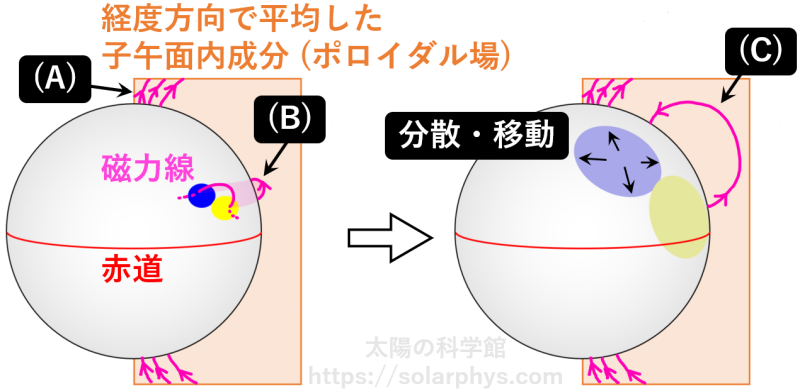
さて、太陽表面の磁場を経度方向で平均すると、極域には 図 18 (A) のような磁場が存在するのでした。極性は第 23 周期前半を想定して描いています。第 23 周期は北半球の先行磁極が正極 (黄色) なので、ジョイの法則に従う対構造が出現すると、その上空の磁力線は
子午面
脚注
[極座標]：半径 \(r\)、余緯度 \(\theta\)、方位角 \(\phi\) の 3 つの値で点を指定する方法を極座標 (球座標) と言います。太陽は大雑把に球対称の天体なので、極座標がよく用いられます。方位角は経度とも言います。余緯度は北極から測った角度ですが、代わりに赤道から測った角度である緯度が用いられることもあります。球を縦に (北極と南極を通るように) 切った平面を子午面と言います。
内 (ポロイダル場) に 図 18 (B) のように寄与します。
表面に現れた対構造は、時間の経過と共に熱対流や差動回転に揉まれて分散しながら、子午面環流に従って極に移動していきます。よって、この対構造によってもたらされた 図 18 (C) の成分はやがて極に集積し、元からあった極域磁場を打ち消す働きをします。たくさんの黒点が形成され、雲散霧消していくうちに、極域磁場はどんどん弱くなり、やがて反転します。
ジョイの法則は統計的に見たときの平均の話でした。上述したバブコック-レイトン機構も、統計的に見たときにそういう傾向がある、という意味での話です。ジョイの法則に従わない黒点もありますし、この機構の効率は悪いと思われます。しかし、黒点の磁場は極域磁場よりもずっと強いので、少しでも相関があれば極域磁場を反転させることができます。
パズルをどう組み立てる？
現在考えられているダイナモモデルの候補の中で、有力な説を 2 つ紹介します。
1 つ目は上述したパズルのピースを、子午面環流を軸にして素朴に組み立てたものであり、磁束輸送ダイナモと呼ばれます。 図 19 に大枠を示しました。まず、Ω 効果によって生成されたトロイダル場の一部が浮力を得て表面まで浮上します。すると、バブコック-レイトン機構によって、子午面内の成分 (ポロイダル場) が生成されます。極に集積して極域磁場を反転させたポロイダル場は、子午面環流によって再び対流層の奥深くまで運ばれます。あるいは一部は極に集積する前に乱流によって深部まで運ばれているかもしれません。
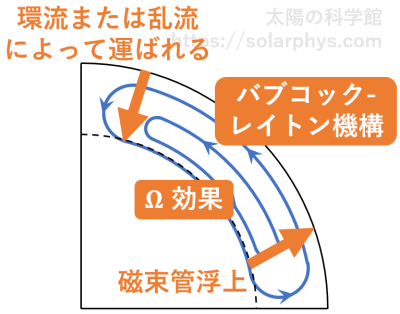
いずれにせよ、底付近にたどり着いたポロイダル場は再び Ω 効果によるトロイダル場生成に使われます。このとき、1 つ前の周期とは逆極性のポロイダル場を種として Ω 効果が働くことになるので、生成されるトロイダル場も逆極性になります。故に、次の周期では表面に浮上してくる対構造の極性も逆になります。
上述した磁束輸送ダイナモをまとめると、Ω 効果がポロイダル場からトロイダル場の生成を司り、磁束管浮上とバブコック-レイトン機構がトロイダル場からポロイダル場の生成を司っていると考えるモデルです。トロイダル場からポロイダル場を生成する機構として、もう 1 つ有力な、しかし具体的にどのような効果を及ぼすのかよく分かっていない候補があります。α (アルファ) 効果と呼ばれるものです。
対流層は乱流状態にあると述べました。この乱流によってトロイダル場が揉まれることによっても、ポロイダル場が生まれる可能性があります。例えば、対流層に横たわるトロイダル場の一部が、図 20 のように対流によって乱されたとします。このとき、コリオリの力が働かなければ、磁力線は図のように Ω のような形になると思われますが、もしコリオリの力が働いたならば、浮き上がった磁力線は図の右のようによじられる可能性があります。
これも統計的な話になります。おそらくトロイダル場は乱流の複雑な動きに揉まれて両方の極性のポロイダル場を生成するでしょう。しかし、仮に対流層奥深くの乱流が、上述したようなひねり運動を頻発させるような統計的性質のものであれば、正味としてバブコック-レイトン機構と同じ極性のポロイダル場が生成されるかもしれません。
しかし、実際の太陽対流層に存在する乱流の統計的性質がどのようなものであるのかを推測するのは難しいため、α 効果がどちらの極性のポロイダル場を生むのか、どれくらいの効率であるのか、という問いに対して自信を持って回答できるわけではありません。
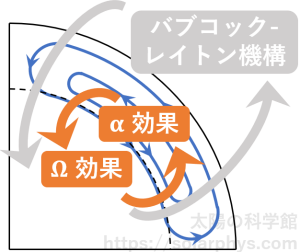
仮に α 効果の効率が良かった場合、Ω 効果と α 効果によって対流層深くでダイナモのループが完結し、磁場が維持されることになります ( 図 21 )。このようなモデルは αΩ ダイナモと呼ばれます。この枠組みを採用した場合、表面で観測されるバブコック-レイトン機構はダイナモに決定的な関与をしているわけではなく、単なる副作用であるということになります。
現在の理解と残る謎
ダイナモモデルの候補を 2 つ紹介しました。これらのことを踏まえて、11 年周期に関する様々な疑問に現在どう答えることができるのか、まとめます。
ヘール-ニコルソンの法則はなぜ表れるのか？
ダイナモ機構の全体構造は 図 22 のようになっています。まず、図の左上のような磁場を正極のポロイダル場と呼ぶことにします。このような磁場が存在すると、主に Ω 効果の働きによってトロイダル場が生まれます。このとき、北半球と南半球の差動回転が反転の関係にあるがゆえに、逆の極性のトロイダル場となります。
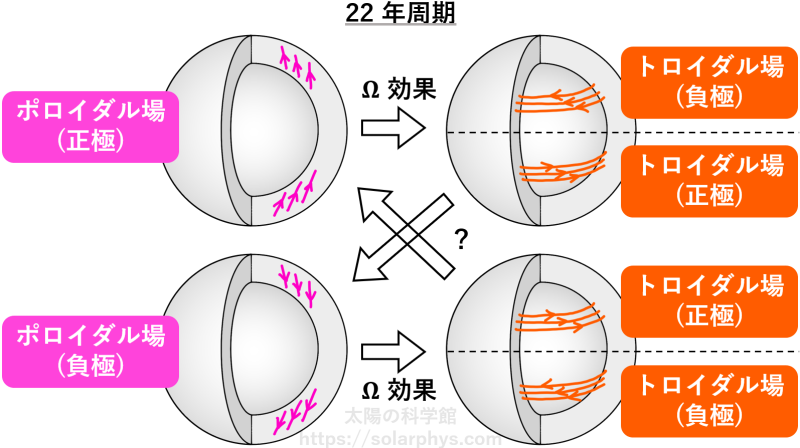
トロイダル場からポロイダル場が生成される過程として、どの機構が重要かはまだ分かっていませんが、例えばバブコック-レイトン機構の場合は、北半球と南半球でコリオリの力が働く向きが逆であるがゆえに、両半球で逆極性のトロイダル場から同極性のポロイダル場が生まれます。このときに生まれるポロイダル場は、前の太陽周期 (11 年) とは逆である、負極のポロイダル場です。
このような機構が繰り返されます。表面にできる黒点対は対流層奥深くにあるトロイダル場の一部が浮上してきたものであると考えれば、黒点対の極性についてのヘール-ニコルソンの法則が再現されていることが分かると思います。
表面の極域磁場が極大期付近で後続磁極の極性に反転することについては、既に述べたように、バブコック-レイトン機構が働いているからであろうと考えられています。
コンピュータによるシミュレーションでは、計算の仕方や設定した対流の強さなどのパラメータによっては、北半球と南半球がそれぞれ勝手な周期、勝手なタイミングで反転を繰り返すような結果が得られることがあります。実際の太陽のように、北半球と南半球が完全にシンクロした蝶形図を描くことは、それほど当たり前のことではないようです。
黒点数が増減を繰り返すのはなぜか？
図 22 のように、対流層の底付近では、
- 強いトロイダル場が存在する時期
- ポロイダル場によって逆極性のトロイダル場が作られ、トロイダル場が反転する時期
が 11 年ごとに繰り返し訪れます。トロイダル場の強さがある閾値を超えると磁束管の浮上が可能になると考えると、前者の時期には浮上がたくさん起こり、後者の時期はトロイダル場の強さが閾値を超えないので、浮上が起こらないことになります。浮上した磁束管が表面から顔を出した場所が黒点なので、従って黒点数が増減すると考えられます。
つまり、黒点数は対流層底付近にあるトロイダル場の強さと相関があると考えられています。
黒点形成領域が赤道に向かって移動するのはなぜか？
磁束管浮上に関する研究の結果からは、対流層の底付近のトロイダル場から生まれた磁束管は、まっずぐ上へ (鉛直方向に) 浮上してくると考えられています。よって、黒点形成領域の赤道方向への移動は、その下に存在するトロイダル場が移動する様子を見ているのだと解釈されます。
磁束輸送ダイナモの枠組みでは、Ω 効果によって高緯度で生成されたトロイダル場が子午面環流に従って徐々に低緯度に運ばれるのではないかと考えられています ( 図 23 )。しかし、対流層深部での熱対流 (乱流) が強い場合は、環流がトロイダル場を運ぶ効率は悪いと考えられるので、確実にそのような機構が働いていると言えるわけではありません。また、上述したように、子午面環流の推定に大きな不確定性があるのも、このシナリオの不安要素の 1 つです。
αΩ ダイナモの枠組みでも、やはり子午面環流が生成されたトロイダル場を低緯度に運んでいる可能性がありますが、もう 1 つ、トロイダル場の移動を説明し得る候補があります。ダイナモ波と呼ばれるものです。
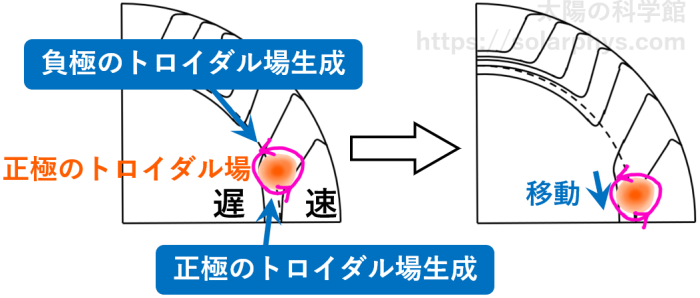
黒点が現れる低緯度領域の対流層底付近では、図 24 のように表面に行くほど速くなるような差動回転の分布をしています。仮に、この対流層底付近の α 効果が、正極のトロイダル場から負極のポロイダル場を生成するような向きに働いているとします。図の左のような正極のトロイダル場の塊が存在した場合、ピンク色で描いたようなポロイダル場が α 効果によって生成されます。
すると、このトロイダル場の低緯度側の端では、差動回転による Ω 効果で正極のトロイダル場が生成されるので、元からあるトロイダル場を強める働きをします。一方で高緯度側の端では、逆に負極のトロイダル場が生成されるので、元からあるトロイダル場を弱める働きをします。その結果、次の瞬間にはトロイダル場は低緯度側に移動しているように見えるはずです (図の右)。この機構が連続的に繰り返し起こることで、子午面環流が無くてもトロイダル場の強い領域は時々刻々と (と言っても 10 年スケールでの話ですが) 移動していきます。
ただし、移動する方向は差動回転の分布と α 効果の性質に大きく依存します。実際の太陽では場所によって様々な向きにダイナモ波が伝搬することが予想されますが、その向きを具体的に推定するのは難しいことです。
黒点が緯度 30 度以内にしかできないのはなぜか？
図 25 は磁束輸送ダイナモのシミュレーション結果の一例です。このシミュレーションは、磁束管浮上の効果と対流による効果、差動回転、子午面流を与えた上で、経度方向に平均した磁場がどのように時間発展するのかを見守る、といった類の数値実験です。上段は対流層の底でのトロイダル場の強さの変遷を色で示したもので、縦軸は緯度、横軸は時間を表します。
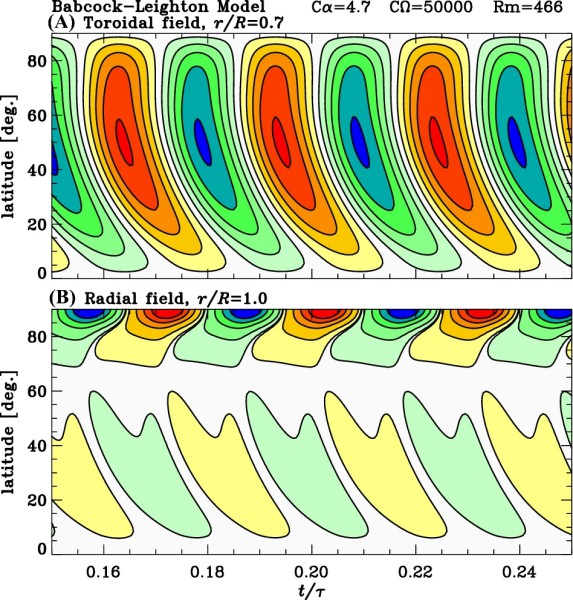
図を見ると、トロイダル場の極性は周期的に反転しており、強い領域が低緯度に向かって移動している様子が再現できていることが分かりますが、トロイダル場は緯度 30 度より高緯度にも存在しています。このような特徴は他のシミュレーションでもしばしば見られます。
磁束管は底のトロイダル場から真っすぐ上に浮上してくるという主張 (詳しくは例えば Fan, 2009 ) を信用するならば、次の 2 つの方針があり得ます。
- 高緯度のトロイダル場を示すシミュレーションはどこかが間違っていて、実際の太陽では低緯度のみに磁束管浮上の閾値を超えるトロイダル場が存在する。
- 実際の太陽でも高緯度に強いトロイダル場が存在するが、何らかの機構が働いて、低緯度でしか浮上磁束管が形成されない。
前者に関連して、例えば子午面環流が対流層下の放射層の深いところまで貫くような分布をしているならば、トロイダル場はもっと低緯度にできるのではないかという研究もあります。子午面環流が実際にそのような分布をしているかについてはよく分かっていません。
後者の機構としては、まず次の可能性が考えられます。高緯度に横たわるポロイダル場の磁力線は、低緯度のものより強く曲がっています。これは高緯度の方が自転軸からの距離が小さいためです。磁力線は曲げられると、真っすぐになろうとする向きに力がかかります (磁気張力)。細長い竹ひごのようなイメージです。高緯度のトロイダル場はこの力が強く働いているため、磁束管の浮上が妨げられているのかもしれません。
ただし、横たわるトロイダル場の一部から磁束管が切り離されて浮上を始める仕組みについては、まだ分かっていないことが多いです。対流層の底に様々な強さの磁束管を置いて浮上する様子を系統的に調べる研究からは、観測される黒点の特徴を再現するためには、初めの磁束管の強さが \(4 \sim 10 \ \text{T}\) 程度ないといけないことが分かっています。しかし、ダイナモの研究で得られるトロイダル場の強さは \(1 \ \text{T}\) 程度と、若干弱めであることが示唆されています。この溝を埋めるための研究の過程で、緯度についての新たな知見も得られるかもしれません (この話題については例えば Fan, 2009 のレビューや Kitchatinov, 2020 を読んでください)。
11 年という周期は何が決めているのか？
バブコック-レイトン機構による磁束輸送ダイナモの枠組みでは、表面で生成されたポロイダル場が対流層深部まで運ばれる効率が周期を決定する主な要因であると考えられます。つまり、子午面環流の速さか、乱流に揉まれて深部まで染み込む効率のどちらかということになります。
αΩ ダイナモの枠組みでは、ダイナモ波が伝わる速さが全体の周期ということになります。この伝搬速度は主に対流層深部での対流の強さに大きく依存します。
どちらのモデルの場合も、周期を調べるには対流層内部での乱流強度の見積もりが不可欠です。今の段階では、どちらのモデルでもあわよくば 10 年の桁数の周期になり得るという見積もり状況であり、それ以上の詳細は分からないことが多いです。
磁場の強さを決めているのは何か？
黒点数の観測は遠い昔から行われています。図 26 はそれらのデータを集め、観測者による違いがなるべく少なくなるような指標に焼き直したデータです。
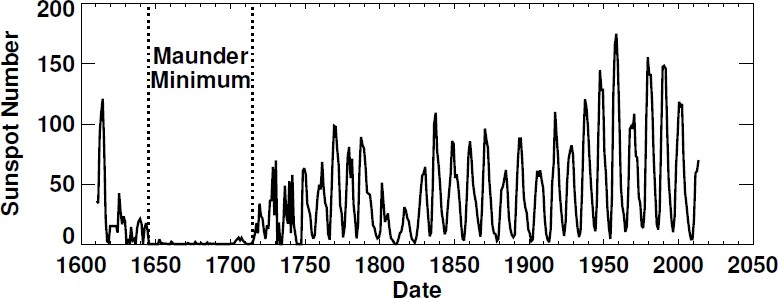
1650 年から 1700 年のあたりでは、黒点が少ない年が続いたようです。この期間はモーンダー極小期と呼ばれます。その後黒点数は周期を描きながら復活していきます。この先どうなるのかは分かりませんが、図を見ると、極大期での黒点数はある程度頭打ちになっているようにも見えます。
上述したダイナモ機構の候補が上手く機能すると、磁場をどんどん増幅するでしょう。しかし、ある程度の磁場の強さになると、磁場生成のループの内のどれかの機構が上手く機能しなくなり、増幅は頭打ちになると考えられます。つまり、太陽の磁場の強さは、ダイナモのループを抑制 (quenching) するような機構がいつ働くかで決まっていると考えます。
磁束輸送ダイナモの枠組みでは、そのような抑制機構の候補としては次のものが挙げられます。バブコック-レイトン機構の要はジョイの法則でした。対流層底のトロイダル場が強くなると浮上する磁束管の強度も増すかもしれません。すると、コリオリの力が磁場の力に負けて上手く働かなくなり、平均的な黒点対の傾き角は小さくなっていくでしょう。このようにして、ポロイダル場を生成する効率が悪くなる可能性があります。
因みに、トロイダル場が弱すぎてもジョイの法則に従わなくなるか、あるいは磁束管浮上が起こらなくなるかの理由でバブコック-レイトン機構が壊れるため、磁束輸送ダイナモが機能する磁場強度の範囲には下限も存在すると考えられます。
一方で、αΩ ダイナモの枠組みでは α 抑制と呼ばれる機構が考えられています。対流層内の磁場が強くなり、そのエネルギーが乱流の運動エネルギーを超えると、
プラズマ
脚注
[プラズマ]：粒子が電子を手放して電荷を持つようになることを電離と言います。太陽内部やコロナは温度が高いので、主な構成元素である水素やヘリウムは、電離してイオンの状態で存在します。電荷を持った粒子を含む気体をプラズマと言います。太陽表面は温度が不十分なので、一部の粒子のみが電離しています。この状態を部分電離と言います。
の流れで磁力線を動かすことはもはやできなくなり、逆に磁力線の存在によって動きが制限されるようになります。こうして乱流の強度は抑えられるはずです。α 効果は乱流によってポロイダル場を生成する機構なので、従って効率が落ちます。
差動回転は 図 13 で示した分布をしていることが分かっていますが、22 年周期の中で回転速度が微妙に、しかし規則的に変化する様子も捉えられています。ねじれ振動 ( torsional oscillation、詳しくは例えば Pipin & Kosovichev, 2019 ) と呼ばれる現象です。今までは問題を簡単にするために、差動回転や子午面環流は定常であると仮定した研究によってモデルが構築されてきましたが、このような変化がダイナモ機構の抑制と関係している可能性も考慮せねばなりません。
大規模シミュレーション
これまでのダイナモ研究では、主に 2.5 次元シミュレーションと呼ばれる手法が用いられてきました。 図 27 (A) にシミュレーションの様子の一例を示します。この類のシミュレーションでは、差動回転や子午面環流、対流による効果を人為的に与えた上で、経度方向で平均した磁場が時間変化する様子を、2 次元の箱の中で計算します。計算する領域は 2 次元ですが、磁場はベクトルの 3 成分について計算するので、 2.5 次元と呼ばれます。
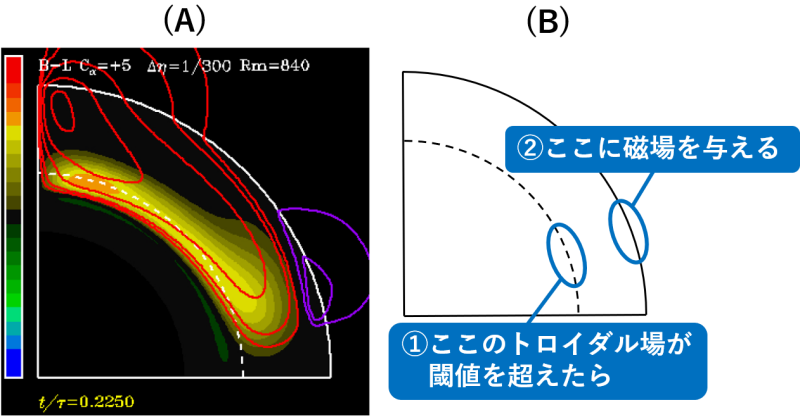
2 次元の箱での計算では、磁束管浮上や α 効果のような複雑な効果は自然には再現できないため、これらも人為的に与えられます。例えばバブコック-レイトン機構を調べるための 2.5 次元シミュレーションでは、 図 27 (B) のように、対流層底のトロイダル場が閾値を超えたら、何らかの関数に従ってその上方の表面付近に磁場の子午面内成分 (ポロイダル場) を与える、というようにして磁束管浮上を模した効果が与えられます。
子午面環流の速さを変えて計算してみる、対流を表す効果のパラメータを様々に変えて計算してみる、別の磁束管浮上の研究から得られた知見を反映させて計算してみる、など様々な工夫を凝らして系統的に調べられてきた結果、実際の太陽で起きている可能性があると多くの研究者に判断されているモデルを上の節で説明したわけです。
コンピュータの計算速度の向上に伴って、2010 年代に入ってからは、3 次元的な箱をコンピュータ上に用意して、差動回転や子午面環流から自分で作り出すような計算をさせる研究が現れ始めました。 図 28 にそのような 3 次元シミュレーションの様子の一例を示します。
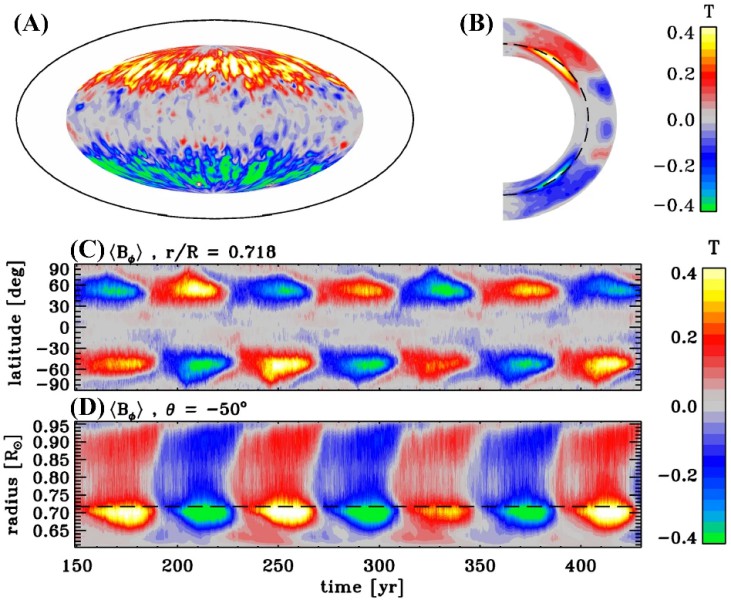
図 28 (C) を見ると、このシミュレーションは周期的な磁場の反転を再現できていることが分かります。しかし、トロイダル場の赤道方向への移動はかすかにしか見られませんし、本来ならば黒点が形成されるはずの低緯度領域には強いトロイダル場が存在しません。
3 次元シミュレーションで人為的に与えるパラメータは、基本的な自転速度と内側から対流層に与える熱量、想定する
プラズマ
脚注
[プラズマ]：粒子が電子を手放して電荷を持つようになることを電離と言います。太陽内部やコロナは温度が高いので、主な構成元素である水素やヘリウムは、電離してイオンの状態で存在します。電荷を持った粒子を含む気体をプラズマと言います。太陽表面は温度が不十分なので、一部の粒子のみが電離しています。この状態を部分電離と言います。
の電気抵抗や粘性の具合です。世界中で複数の研究グループがそれぞれ独自の手法で 3 次元シミュレーションのプログラムを開発しています。同じようなパラメータを与えて計算させても、計算方法が違うと計算結果も異なってしまうというのが現状のようです。研究によって、周期的な磁場反転を示すもの、反転はするがタイミングはまちまちで周期的ではないもの、反転を示さないものなど、様々な計算結果が見られます。
現在の 3 次元シミュレーションの精度だと、磁束管浮上が要であるバブコック-レイトン機構を再現することはできません。つまり、3 次元シミュレーション内の磁場は αΩ ダイナモのような機構で生成されていることになります。しかし、現段階では実際の対流層内部の乱流状態をどこまで再現しているかは分からないという状況に見受けられます。
3 次元シミュレーション結果の解析からダイナモモデルの具体的な議論ができるようにするためには、第一にコンピュータの計算速度の更なる向上、第二に計算手法の発展、更には計算結果の解析手法の発展が期待されます。
参考文献
記事全体として参考にしたレビュー (書籍)
- Charbonneau, P. (2020). Dynamo models of the solar cycle. Living Reviews in Solar Physics, 17, 4 .
- 桜井隆 & 横山央明. (2009). 活動周期とダイナモ機構. 桜井隆, 小島正宜, 小杉健郎 & 柴田一成 編, シリーズ 現代の天文学 第 10 巻 『太陽』 (東京: 日本評論社), 第 6 章.
引用した文献
- Fan, Y. (2009). Magnetic fields in the solar convection zone. Living Reviews in Solar Physics, 6, 4 .
- Gizon, L., Cameron, R. H., Pourabdian, M., Liang, Z.-C., Fournier, D., Birch, A. C. and Hanson, C. S. (2020). Meridional flow in the Sun’s convection zone is a single cell in each hemisphere. Science, 368, 1469-1472 .
- Hathaway, D. H. (2015). The solar cycle. Living Reviews in Solar Physics, 12, 4 .
- Kitchatinov, L. L. (2020). Flux tubes forming instability near the base of the rotating convection zone: A possible explanation for the low latitudes of sunspots. The Astrophysical Journal, 893, 131 .
- Pipin, V. V. and Kosovichev, A. G. (2019). On the origin of solar torsional oscillations and extended solar cycle. The Astrophysical Journal, 887, 215 .
- Stevenson, D. J. (2010). Planetary magnetic fields: achievements and prospects. Space Science Reviews, 152, 651-664 .